Website durchsuchen

Ellipsoid

Kugel (oben, a=4),
Rotationsellipsoid (unten links, {\displaystyle a=b=5,\ c=3}),
triaxiales Ellipsoid (unten rechts, {\displaystyle a=4{,}5,\ b=6,\ c=3})

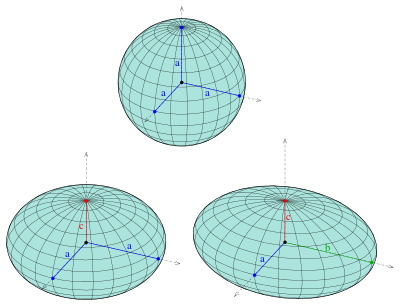
Ein Ellipsoid ist die 3-dimensionale Entsprechung einer Ellipse. So wie sich eine Ellipse als affines Bild des Einheitskreises auffassen lässt, gilt:

Die einfachsten affinen Abbildungen sind die Skalierungen der kartesischen Koordinaten. Sie liefern Ellipsoide mit Gleichungen

Solch ein Ellipsoid ist punktsymmetrisch zum Punkt (0,0,0), dem Mittelpunkt des Ellipsoids. Die Zahlen a,b,c sind analog zu einer Ellipse die Halbachsen des Ellipsoids und die Punkte (\pm a,0,0),(0,\pm b,0),(0,0,\pm c) seine 6 Scheitelpunkte.

Alle Ellipsoide {\displaystyle E_{abc}} sind symmetrisch zu jeder der drei Koordinatenebenen. Beim Rotationsellipsoid kommt noch die Rotationssymmetrie bezüglich der Rotationsachse hinzu. Eine Kugel ist zu jeder Ebene durch den Mittelpunkt symmetrisch.

Jupiters Durchmesser von Pol zu Pol ist deutlich kleiner als am Äquator (zum Vergleich roter Kreis)

Angenäherte Beispiele für Rotationsellipsoide sind der Rugbyball und abgeplattete rotierende Himmelskörper, etwa die Erde oder andere Planeten (Jupiter), Sonnen oder Galaxien. Elliptische Galaxien und Zwergplaneten (z.B. (136108) Haumea) können auch triaxial sein.

In der Linearen Optimierung werden Ellipsoide in der Ellipsoid-Methode verwendet.

Parameterdarstellung

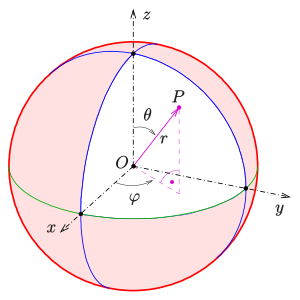
Kugelkoordinaten r,\theta ,\varphi eines Punktes und kartesisches Koordinatensystem

Die Punkte auf der Einheitskugel können wie folgt parametrisiert werden (siehe Kugelkoordinaten):

{\displaystyle {\begin{array}{cll}x&=&\sin \theta \cdot \cos \varphi \\y&=&\sin \theta \cdot \sin \varphi \\z&=&\cos \theta \end{array}}}

Für den Winkel \theta (von der z-Achse aus gemessen) gilt 0\leq \theta \leq \pi . Für den Winkel \varphi (von der x-Achse aus gemessen) gilt {\displaystyle 0\leq \varphi <2\pi }.

Skaliert man die einzelnen Koordinaten mit den Faktoren a,b,c, so ergibt sich eine Parameterdarstellung des Ellipsoids {\displaystyle E_{abc}}:

{\displaystyle {\begin{array}{cll}x&=&a\cdot \sin \theta \cdot \cos \varphi \\y&=&b\cdot \sin \theta \cdot \sin \varphi \\z&=&c\cdot \cos \theta \end{array}}}

mit 0\leq \theta \leq \pi und {\displaystyle 0\leq \varphi <2\pi .}

Volumen

Das Volumen des Ellipsoids {\displaystyle E_{abc}} ist

V={\frac {4}{3}}\pi abc.

Eine Kugel mit Radius r hat das Volumen {\displaystyle V={\tfrac {4}{3}}\pi r^{3}.}

Herleitung

Der Schnitt des Ellipsoids {\displaystyle E_{abc}} mit einer Ebene in der Höhe z ist die Ellipse {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1-{\frac {z^{2}}{c^{2}}} mit den Halbachsen

a'=a{\sqrt {1-{\frac {z^{2}}{c^{2}}}}},\ b'=b{\sqrt {1-{\frac {z^{2}}{c^{2}}}}}.

Der Flächeninhalt dieser Ellipse ist A(z)=\pi a'b'=\pi ab(1-{\frac {z^{2}}{c^{2}}}). Das Volumen ergibt sich dann aus

{\displaystyle \int _{-c}^{c}A(z)\ \mathrm {d} z=\pi ab\int _{-c}^{c}(1-{\frac {z^{2}}{c^{2}}})\ \mathrm {d} z={\frac {4}{3}}\pi abc.}

Oberfläche

Oberfläche eines Rotationsellipsoids

→ Hauptartikel: Rotationsellipsoid

Die Oberfläche eines abgeplatteten Rotationsellipsoids {\displaystyle E_{aac}} mit a>c ist

A=2\pi a\left(a+{\frac {c^{2}}{\sqrt {a^{2}-c^{2}}}}\,\operatorname {arsinh} \left({\frac {\sqrt {a^{2}-c^{2}}}{c}}\right)\right),

die des verlängerten Ellipsoids (c>a)

A=2\pi a\left(a+{\frac {c^{2}}{\sqrt {c^{2}-a^{2}}}}\,\operatorname {arcsin} \left({\frac {\sqrt {c^{2}-a^{2}}}{c}}\right)\right).

Eine Kugel mit Radius r hat die Oberfläche A=4\pi r^{2}.

Oberfläche des triaxialen Ellipsoids

Die Oberfläche eines triaxialen Ellipsoids lässt sich nicht mit Hilfe von Funktionen ausdrücken, die man als elementar ansieht, wie z.B. \operatorname {arsinh} oder \arcsin oben beim Rotationsellipsoid. Die Flächenberechnung gelang Adrien-Marie Legendre mit Hilfe der elliptischen Integrale. Sei a>b>c. Schreibt man

k={\frac {a}{b}}{\frac {\sqrt {b^{2}-c^{2}}}{\sqrt {a^{2}-c^{2}}}} und \varphi =\arcsin {\frac {\sqrt {a^{2}-c^{2}}}{a}},

so lauten die Integrale

E(k,\varphi )=\int _{0}^{\sin \varphi }{\sqrt {\frac {1-k^{2}x^{2}}{1-x^{2}}}}\ \mathrm {d} x und F(k,\varphi )=\int _{0}^{\sin \varphi }{\frac {1}{{\sqrt {1-x^{2}}}{\sqrt {1-k^{2}x^{2}}}}}\ \mathrm {d} x.

Die Oberfläche hat mit E und F nach Legendre den Wert

A=2\pi c^{2}+{\frac {2\pi b}{\sqrt {a^{2}-c^{2}}}}\left(c^{2}F(k,\varphi )+(a^{2}-c^{2})E(k,\varphi )\right).

Werden die Ausdrücke für k und \varphi sowie die Substitutionen

{\displaystyle u:={\frac {\sqrt {a^{2}-c^{2}}}{a}}}  und  {\displaystyle v:={\frac {\sqrt {b^{2}-c^{2}}}{b}}}

in die Gleichung für A eingesetzt, so ergibt sich die Schreibweise

A=2\pi c^{2}+2\pi ab\int _{0}^{1}{\frac {1-u^{2}v^{2}x^{2}}{{\sqrt {1-u^{2}x^{2}}}{\sqrt {1-v^{2}x^{2}}}}}\ \mathrm {d} x.

Von Knud Thomsen stammt die integralfreie Näherungsformel

{\displaystyle A\approx 4\pi \left({\frac {(ab)^{\frac {8}{5}}+(ac)^{\frac {8}{5}}+(bc)^{\frac {8}{5}}}{3}}\right)^{\frac {5}{8}}.}

Die maximale Abweichung vom exakten Resultat beträgt weniger als 1,2 %.

Im Grenzfall eines vollständig plattgedrückten Ellipsoids \left(c\to 0\right) streben alle drei angegebenen Formeln für A gegen 2\pi ab, den doppelten Wert des Flächeninhalts einer Ellipse mit den Halbachsen a und b.

Anwendungsbeispiel zu den Formeln

Der Planet Jupiter ist wegen den durch die schnelle Rotation wirkenden Zentrifugalkräfte an den Polen deutlich flacher als am Äquator und haben annähernd die Form eines Rotationsellipsoids.

Der Jupiter hat den Äquatordurchmesser 142984 km und den Poldurchmesser 133708 km. Also gilt für die Halbachsen {\displaystyle a=b=71492\ \mathrm {km} } und {\displaystyle c=66854\ \mathrm {km} }. Die Masse des Jupiter beträgt etwa 1,899 · 1027 kg. Daraus ergibt sich mithilfe der oben genannten Formeln für das Volumen, die mittlere Dichte und die Oberfläche:

Das ist etwa 1321-mal so viel wie das Volumen der Erde.
Der Jupiter hat also insgesamt eine etwas höhere Dichte als Wasser unter Standardbedingungen.
Das ist etwa 121-mal so viel wie die Oberfläche der Erde.

Ebene Schnitte

Eigenschaften

Ebener Schnitt eines Ellipsoids

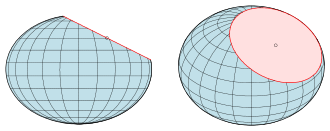
Der Schnitt eines Ellipsoids mit einer Ebene ist

Der erste Fall folgt aus der Tatsache, dass eine Ebene eine Kugel in einem Kreis schneidet und ein Kreis bei einer affinen Abbildung in eine Ellipse übergeht. Dass einige der Schnittellipsen Kreise sind, ist bei einem Rotationsellipsoid offensichtlich: Alle ebenen Schnitte, die wenigstens 2 Punkte enthalten und deren Ebenen senkrecht zur Rotationsachse sind, sind Kreise. Dass aber auch jedes 3-achsige Ellipsoid viele Kreise enthält, ist nicht offensichtlich und wird in Kreisschnittebene erklärt.

Der wahre Umriss eines beliebigen Ellipsoids ist sowohl bei Parallelprojektion als auch bei Zentralprojektion ein ebener Schnitt, also eine Ellipse (siehe Bilder).

Bestimmung einer Schnittellipse

Ebener Schnitt eines Ellipsoids

Gegeben: Ellipsoid {\displaystyle \ {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\ } und eine Ebene mit der Gleichung {\displaystyle \ n_{x}x+n_{y}y+n_{z}z=d\ ,} die das Ellipsoid in einer Ellipse schneidet.
Gesucht: Drei Vektoren {\vec {f}}_{0} (Mittelpunkt) und {\displaystyle {\vec {f}}_{1},\;{\vec {f}}_{2}} (konjugierte Vektoren) so, dass die Schnittellipse durch die Parameterdarstellung

{\displaystyle {\vec {x}}={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t\quad }

beschrieben werden kann (siehe Ellipse).

Ebener Schnitt der Einheitskugel

Lösung: Die Skalierung {\displaystyle \ u={\frac {x}{a}}\ ,\ v={\frac {y}{b}}\,\ w={\frac {z}{c}}\ } führt das Ellipsoid in die Einheitskugel {\displaystyle u^{2}+v^{2}+w^{2}=1\ } und die gegebene Ebene in die Ebene mit der Gleichung {\displaystyle \ n_{x}au+n_{y}bv+n_{z}cw=d\ } über. Die Hesse-Normalform der neuen Ebene sei {\displaystyle \ m_{u}u+m_{v}v+m_{w}w=\delta \ } mit dem Normaleneinheitsvektor {\displaystyle \;{\vec {m}}=(m_{u},m_{v},m_{w})^{T}\;.} Dann ist
der Mittelpunkt des Schnittkreises {\displaystyle {\vec {e}}_{0}=\delta \;{\vec {m}}\;} und dessen Radius {\displaystyle \;\rho ={\sqrt {1-\delta ^{2}}}\;.}
Falls {\displaystyle \ m_{w}=\pm 1\ } ist, sei {\displaystyle \quad {\vec {e}}_{1}=(\rho ,0,0)^{T}\;,\ {\vec {e}}_{2}=(0,\rho ,0)^{T}\;.} (Die Ebene ist horizontal!)
Falls {\displaystyle \ m_{w}\neq \pm 1} ist, sei {\displaystyle \quad {\vec {e}}_{1}=\rho \,{\frac {(m_{v},-m_{u},0)^{T}}{\sqrt {m_{u}^{2}+m_{v}^{2}}}}\;,\ {\vec {e}}_{2}={\vec {m}}\times {\vec {e}}_{1}\ .}
Die Vektoren {\displaystyle {\vec {e}}_{1},{\vec {e}}_{2}} sind in jedem Fall zwei in der Schnittebene liegende orthogonale Vektoren der Länge \rho (Kreisradius), d.h., der Schnittkreis wird durch die Parameterdarstellung {\displaystyle \;{\vec {u}}={\vec {e}}_{0}+{\vec {e}}_{1}\cos t+{\vec {e}}_{2}\sin t\;} beschrieben.

Macht man nun die obige Skalierung (affine Abbildung) rückgängig, so wird die Einheitskugel wieder zum gegebenen Ellipsoid und man erhält aus den Vektoren {\displaystyle {\vec {e}}_{0},{\vec {e}}_{1},{\vec {e}}_{2}} die gesuchten Vektoren {\vec {f}}_{0},{\vec {f}}_{1},{\vec {f}}_{2}, mit denen man die Schnittellipse beschreiben kann. Wie man daraus die Scheitelpunkte der Ellipse und damit ihre Halbachsen bestimmt, wird unter Ellipse erklärt.

Beispiel: Die Bilder gehören zu dem Beispiel mit {\displaystyle \;a=4,\;b=5,\;c=3\;} und der Schnittebene {\displaystyle \;x+y+z=5\;.} Das Bild des Ellipsoidschnittes ist eine senkrechte Parallelprojektion auf eine Ebene parallel zur Schnittebene, d.h., die Ellipse erscheint bis auf eine uniforme Skalierung in wahrer Gestalt. Man beachte, dass {\vec {f}}_{0} hier im Gegensatz zu {\displaystyle {\vec {e}}_{0}} nicht auf der Schnittebene senkrecht steht. Die Vektoren {\displaystyle {\vec {f}}_{1},\;{\vec {f}}_{2}} sind hier im Gegensatz zu {\displaystyle {\vec {e}}_{1},\;{\vec {e}}_{2}\;}nicht orthogonal.

Fadenkonstruktion

Fadenkonstruktion einer Ellipse
{\displaystyle |S_{1}S_{2}|=} Länge des Fades (rot)
Fadenkonstruktion eines Ellipsoids
Fadenkonstruktion: Bestimmung der Halbachsen

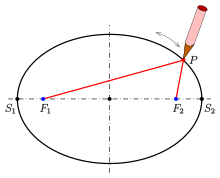
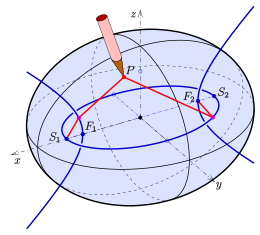
Die Fadenkonstruktion eines Ellipsoids ist eine Übertragung der Idee der Gärtnerkonstruktion einer Ellipse (siehe Abbildung). Eine Fadenkonstruktion eines Rotationsellipsoids ergibt sich durch Konstruktion der Meridian-Ellipsen mit Hilfe eines Fadens.

Punkte eines 3-achsigen Ellipsoids mit Hilfe eines gespannten Fadens zu konstruieren ist etwas komplizierter. Wolfgang Boehm schreibt in dem Artikel Die Fadenkonstruktion der Flächen zweiter Ordnung die Grundidee der Fadenkonstruktion eines Ellipsoids dem schottischen Physiker James Clerk Maxwell (1868) zu. Otto Staude hat in Arbeiten 1882, 1886, 1898 die Fadenkonstruktion dann auf Quadriken verallgemeinert. Die Fadenkonstruktion für Ellipsoide und Hyperboloide wird auch in dem Buch Anschauliche Geometrie von David Hilbert und Stefan Cohn-Vossen beschrieben. Auch Sebastian Finsterwalder beschäftigte sich 1886 mit diesem Thema.

Konstruktionsschritte
(1) Man wähle eine Ellipse und eine Hyperbel, die ein Paar von Fokalkegelschnitten bilden:
Ellipse: {\displaystyle \quad E(\varphi )=(a\cos \varphi ,b\sin \varphi ,0)\ } und
Hyperbel: {\displaystyle \ H(\psi )=(c\cosh \psi ,0,b\sinh \psi )\quad ,\ c^{2}=a^{2}-b^{2}\ }
mit den Scheitelpunkten und Brennpunkten der Ellipse
{\displaystyle S_{1}=(a,0,0),\ F_{1}=(c,0,0),\ F_{2}=(-c,0,0),\ S_{2}=(-a,0,0)\;.}
und einen Faden (in der Abbildung Bild rot) der Länge l.
(2) Man befestige das eine Ende des Fadens im Scheitelpunkt S_{1} und das andere Ende im Brennpunkt F_{2}. Der Faden wird in einem Punkt P so gespannt gehalten, dass der Faden von hinten auf der Hyperbel und von vorn auf der Ellipse gleiten kann (siehe Abbildung). Der Faden geht über denjenigen Hyperbelpunkt, mit dem die Entfernung von P nach S_{1} über einen Hyperbelpunkt minimal wird. Analoges gilt für den Fadenteil von P nach F_{2} über einen Ellipsenpunkt.
(3) Wählt man den Punkt P so, dass er positive y- und z-Koordinaten hat, so ist P ein Punkt des Ellipsoids mit der Gleichung
{\displaystyle {\frac {x^{2}}{r_{x}^{2}}}+{\frac {y^{2}}{r_{y}^{2}}}+{\frac {z^{2}}{r_{z}^{2}}}=1\quad } und
{\displaystyle r_{x}={\frac {1}{2}}(l-a+c)\ ,\quad r_{y}={\sqrt {r_{x}^{2}-c^{2}}}\ ,\quad r_{z}={\sqrt {r_{x}^{2}-a^{2}}}\ .}
(4) die restlichen Punkte des Ellipsoids erhält man durch geeignetes Umspannen des Fadens an den Fokalkegelschnitten.

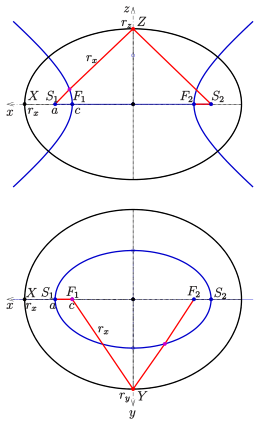
Die Gleichungen für die Halbachsen des erzeugten Ellipsoids ergeben sich, wenn man den Punkt P in die beiden Scheitelpunkte {\displaystyle Y=(0,r_{y},0),\ Z=(0,0,r_{z})} fallen lässt:

Aus der unteren Zeichnung erkennt man, dass F_1,F_2 auch die Brennpunkte der Äquatorellipse sind. D. h.: Die Äquatorellipse ist konfokal zur gegebenen Fokalellipse. Also ist {\displaystyle l=2r_{x}+(a-c)}, woraus sich {\displaystyle r_{x}={\frac {1}{2}}(l-a+c)} ergibt. Ferner erkennt man, dass {\displaystyle r_{y}^{2}=r_{x}^{2}-c^{2}} ist.
Aus der oberen Zeichnung ergibt sich: S_1,S_2 sind die Brennpunkte der Ellipse in der x-z-Ebene und es gilt {\displaystyle r_{z}^{2}=r_{x}^{2}-a^{2}}.

Umkehrung:
Möchte man ein durch seine Gleichung gegebenes 3-achsiges Ellipsoid {\mathcal E} mit den Halbachsen {\displaystyle r_{x},r_{y},r_{z}} konstruieren, so lassen sich aus den Gleichungen im Schritt (3) die für die Fadenkonstruktion nötigen Parameter {\displaystyle a,b,l} berechnen. Für die folgenden Überlegungen wichtig sind die Gleichungen

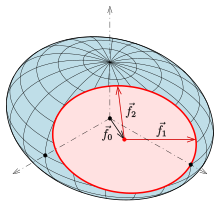
(5){\displaystyle :\ r_{x}^{2}-r_{y}^{2}=c^{2},\quad r_{x}^{2}-r_{z}^{2}=a^{2},\quad r_{y}^{2}-r_{z}^{2}=a^{2}-c^{2}=b^{2}\ .}

Konfokale Ellipsoide:
Ist {\displaystyle {\mathcal {\overline {E}}}} ein zu {\mathcal E} konfokales Ellipsoid mit den Quadraten der Halbachsen

(6){\displaystyle :\ {\overline {r}}_{x}^{2}=r_{x}^{2}-\lambda ,\quad {\overline {r}}_{y}^{2}=r_{y}^{2}-\lambda ,\quad {\overline {r}}_{z}^{2}=r_{z}^{2}-\lambda \;,}

so erkennt man aus den vorigen Gleichungen, dass die zu {\displaystyle {\mathcal {\overline {E}}}} gehörigen Fokalkegelschnitte für die Fadenerzeugung dieselben Halbachsen a,b,c wie die von {\mathcal E} besitzen. Deshalb fasst man – analog der Rolle der Brennpunkte bei der Fadenerzeugung einer Ellipse – die Fokalkegelschnitte eines 3-achsigen Ellipsoids als deren unendlich viele Brennpunkte auf und nennt sie Fokalkurven des Ellipsoids.

Auch die Umkehrung ist richtig: Wählt man einen zweiten Faden der Länge \overline l und setzt {\displaystyle \lambda =r_{x}^{2}-{\overline {r}}_{x}^{2}}, so gilt {\displaystyle {\overline {r}}_{y}^{2}=r_{y}^{2}-\lambda ,\ {\overline {r}}_{z}^{2}=r_{z}^{2}-\lambda \;.} D. h.: Die beiden Ellipsoide sind konfokal.

Grenzfall Rotationsellipsoid:
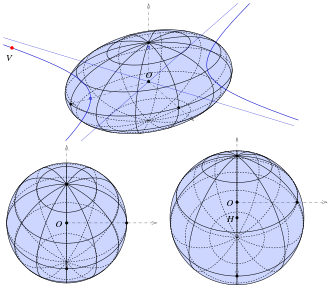
Im Fall a=c ist {\displaystyle \ S_{1}=F_{1},\;S_{2}=F_{2}\;}, d.h., die Fokalellipse artet in eine Strecke und die Hyperbel in zwei Strahlen auf der x-Achse aus. Das Ellipsoid ist dann ein Rotationsellipsoid mit der x-Achse als Rotationsachse. Es ist {\displaystyle \ r_{x}={\tfrac {l}{2}},\;r_{y}=r_{z}={\sqrt {r_{x}^{2}-c^{2}}}\ }.

Unten: Parallelprojektion und Zentralprojektion eines 3-achsigen Ellipsoids, wo der scheinbare Umriss ein Kreis ist

Eigenschaften der Fokalhyperbel:
Betrachtet man ein Ellipsoid von einem außerhalb gelegenen Punkt V auf der zugehörigen Fokalhyperbel aus, so erscheint der Umriss des Ellipsoids als Kreis. Oder, anders ausgedrückt: Die Tangenten des Ellipsoids durch V bilden einen senkrechten Kreiskegel, dessen Rotationsachse Tangente in V an die Hyperbel ist. Lässt man den Augpunkt V ins Unendliche laufen, entsteht die Ansicht einer senkrechten Parallelprojektion mit einer Asymptote der Fokalhyperbel als Projektionsrichtung. Die wahre Umrisskurve auf dem Ellipsoid ist im Allgemeinen kein Kreis.
In der Abbildung ist unten links eine Parallelprojektion eines 3-achsigen Ellipsoids (Halbachsen: 60,40,30) in Richtung einer Asymptote und unten rechts eine Zentralprojektion mit Zentrum V auf der Fokalhyperbel und Hauptpunkt H auf der Tangente an die Hyperbel in V dargestellt. In beiden Projektionen sind die scheinbaren Umrisse Kreise. Links ist das Bild des Koordinatenursprungs O der Mittelpunkt des Umrisskreises, rechts ist der Hauptpunkt H der Mittelpunkt.

Die Fokalhyperbel eines Ellipsoids schneidet das Ellipsoid in seinen vier Nabelpunkten.

Eigenschaft der Fokalellipse:
Die Fokalellipse mit ihrem Inneren kann als Grenzfläche der durch a,b bestimmten Schar von konfokalen Ellipsoide für {\displaystyle \;r_{z}\to 0\;} als unendlich dünnes Ellipsoid angesehen werden. Es ist dann >{\displaystyle \;r_{x}=a,\;r_{y}=b,\;l=3a-c\;.}

Ellipsoid in beliebiger Lage

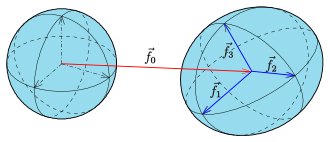
Ellipsoid als affines Bild der Einheitskugel

Parameterdarstellung

Eine affine Abbildung lässt sich durch eine Parallelverschiebung um {\vec {f}}_{0} und eine reguläre 3×3-Matrix A beschreiben:

{\displaystyle {\vec {x}}\mapsto {\vec {f}}_{0}+A{\vec {x}}={\vec {f}}_{0}+x{\vec {f}}_{1}+y{\vec {f}}_{2}+z{\vec {f}}_{3}},

wobei {\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3} die Spaltenvektoren der Matrix A sind.

Die Parameterdarstellung eines beliebigen Ellipsoids ergibt sich aus der obigen Parameterdarstellung der Einheitskugel und der Beschreibung einer affinen Abbildung:

{\vec {x}}(\theta ,\varphi )={\vec {f}}_{0}+{\vec {f}}_{1}\cos \theta \cos \varphi +{\vec {f}}_{2}\cos \theta \sin \varphi +{\vec {f}}_{3}\sin \theta ,\quad -\pi /2\leq \theta \leq \pi /2,\ 0\leq \varphi <2\pi

Umgekehrt gilt: Wählt man einen Vektor {\vec {f}}_{0} beliebig und die Vektoren {\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3} beliebig, aber linear unabhängig, so beschreibt die obige Parameterdarstellung in jedem Fall ein Ellipsoid. Bilden die Vektoren {\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3} ein Orthogonalsystem, so sind die Punkte {\vec {f}}_{0}\pm {\vec {f}}_{i},\ i=1,2,3 die Scheitelpunkte des Ellipsoids und |{\vec {f}}_{1}|,|{\vec {f}}_{2}|,|{\vec {f}}_{3}| die zugehörigen Halbachsen.

Ein Normalenvektor im Punkt {\vec {x}}(\theta ,\varphi ) ist

{\vec {n}}(\theta ,\varphi )={\vec {f}}_{2}\times {\vec {f}}_{3}\cos \theta \cos \varphi +{\vec {f}}_{3}\times {\vec {f}}_{1}\cos \theta \sin \varphi +{\vec {f}}_{1}\times {\vec {f}}_{2}\sin \theta .

Zu einer Parameterdarstellung eines beliebigen Ellipsoids lässt sich auch eine implizite Beschreibung F(x,y,z)=0 angeben. Für ein Ellipsoid mit Mittelpunkt im Koordinatenursprung, d.h. {\vec {f}}_{0}=(0,0,0)^{T}, ist

F(x,y,z)=\operatorname {det} ({\vec {x}},{\vec {f}}_{2},{\vec {f}}_{3})^{2}\;+\;\operatorname {det} ({\vec {f}}_{1},{\vec {x}},{\vec {f}}_{3})^{2}\;+\;\operatorname {det} ({\vec {f}}_{1},{\vec {f}}_{2},{\vec {x}})^{2}\;-\;\operatorname {det} ({\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3})^{2}=0

eine implizite Darstellung.

Bemerkung: Das durch obige Parameterdarstellung beschriebene Ellipsoid ist in dem eventuell schiefen Koordinatensystem {\vec {f}}_{0} (Koordinatenursprung), {\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3} (Basisvektoren) die Einheitskugel.

Ellipsoid als Quadrik

→ Hauptartikel: Quadrik

Ein beliebiges Ellipsoid mit Mittelpunkt {\vec {f}}_{0} lässt sich als Lösungsmenge einer Gleichung

{\displaystyle ({\vec {x}}-{\vec {f}}_{0})^{\top }A\,({\vec {x}}-{\vec {f}}_{0})=1}

schreiben, wobei A eine positiv definite Matrix ist.

Die Eigenvektoren der Matrix A bestimmen die Hauptachsenrichtungen des Ellipsoids und die Eigenwerte von A sind die Kehrwerte der Quadrate der Halbachsen: {\displaystyle a^{-2}}, {\displaystyle b^{-2}} und c^{{-2}}.

Ellipsoid in der projektiven Geometrie

Schließt man den 3-dimensionalen affinen Raum und die einzelnen Quadriken projektiv durch eine Fernebene bzw. Fernpunkte ab, so sind die folgenden Quadriken projektiv äquivalent, d.h., es gibt jeweils eine projektive Kollineation, die die eine Quadrik in die andere überführt:

Literatur

Siehe auch

Trenner
Basierend auf einem Artikel in: Extern Wikipedia.de
Seitenende
Seite zurück
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.07. 2023