
Elliptisches Integral
Ein elliptisches Integral ist ein Integral vom Typ
wobei
eine rationale
Funktion in zwei Variablen
und
ein Polynom
dritten oder vierten Grades ohne mehrfache Nullstelle
ist. Das Integral heißt elliptisch, weil Integrale dieser Form bei der
Berechnung des Umfangs
von Ellipsen
und der Oberfläche
von Ellipsoiden auftreten. Auch
in der Physik gibt es weitreichende Anwendungen.
Elliptische Integrale lassen sich im Allgemeinen nicht durch elementare Funktionen darstellen, sie können aber durch Umformungen in eine Summe von elementaren Funktionen und Integralen der unten beschriebenen Form überführt werden. Diese Integrale heißen elliptische Integrale erster, zweiter und dritter Art.
- I. Art:
- II. Art:
- III. Art:
Dabei ist
Zum Teil wird in der Literatur auch der Parameter
statt
in den Funktionsaufruf eingesetzt und der Definitionsbereich auf
erweitert.
Vollständige elliptische Integrale
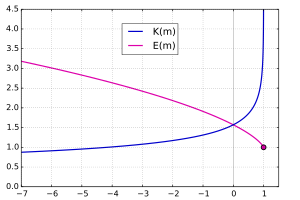
Definition der vollständigen elliptischen Integrale
Die Integrale mit unterer Integralgrenze 0 nennt man unvollständige
elliptische Integrale. Ist zusätzlich die obere Integralgrenze ,
spricht man im Falle der I. und II. Art von vollständigen elliptischen
Integralen. Die vollständigen elliptischen Integrale I. und II. Art stehen
im direkten Bezug zur Gauß’schen
hypergeometrischen Funktion
.
In der nachfolgenden Tabelle sind die vollständigen elliptischen Integrale in
der Integraldarstellung mit den Parametern
und
dargestellt. Die Jacobi-Form lässt sich mit der Substitution
in die Legendre-Normalform überführen. In den Funktions-Bibliotheken von Matlab, Wolfram-Alpha, Mathematica, Python (SciPy) und GNU
Octave ist der Parameter
in Verwendung.
| Konvention mit Parameter |
Konvention mit Parameter | |
|---|---|---|
| I. Art: Jacobi-Form | ||
| I. Art: Legendre-Normalform | ||
| II. Art: Jacobi-Form | ||
| II. Art: Legendre-Normalform | ||
| III. Art: Jacobi-Form | ||
| III. Art: Legendre-Normalform |
Definition der komplementären elliptischen Integrale
Die komplementären vollständigen elliptischen Integrale
und
sind mit der komplementären Variable
wie im Folgenden dargestellt definiert.
Darstellung per Potenzreihe
Die vollständigen elliptischen Integrale lassen sich als Potenzreihe
darstellen.
Die angegebenen Potenzreihen können zur numerischen Auswertung verwendet werden.
Es ist jedoch darauf zu achten, dass die Konvergenz vom Argument
abhängig ist. Die Verwendung von Potenzreihen ist bezüglich der Rechenzeit nicht
die effizienteste Methode zur numerischen Auswertung. Ist in einer
physikalischen Anwendung klar, dass das Argument
in einem bezüglich der Genauigkeit geeignetem Bereich liegt, so bietet die
Potenzreihen-Darstellung im Sinne der Linearisierung
eine nützliche Methode zur Angabe von Näherungslösungen oder Faustformeln.
Beweis für die Potenzreihen:
Es gelten diese beiden binomischen Maclaurin-Reihen für |kx| < 1:
Zusätzlich ist jenes Integral für alle Zahlen n ∈ ℕ₀ gültig:
Deswegen gilt für das vollständige elliptische Integral erster Art:
Und für das vollständige elliptische Integral zweiter Art gilt:
Darstellung per unendlichem Produkt
In der folgenden Tabelle sind Produktdarstellungen des vollständigen
elliptischen Integrals 1. Art und des komplementären elliptischen Integrals 1.
Art angegeben. Oftmals wird auch die komplementäre Variable
zur kompakteren Darstellung verwendet. Auffällig ist die Vertauschung von
und
bezüglich der beiden Produktformeln beim Vergleich zum Komplementär.
| Vollständiges elliptisches Integral I. Art | Komplementäres elliptisches Integral I. Art | |
|---|---|---|
| Anfangswert | ||
| Rekursionsgleichung | ||
| Produktformeln |
Darstellung per AGM-Algorithmus
Neben den Potenzreihen existiert eine Darstellung als Grenzwert des
iterierten arithmetisch-geometrischen
Mittelwertes (AGM-Algorithmus). Im Folgenden stellt
den arithmetischen
Mittelwert,
den geometrischen
Mittelwert und
eine Hilfsvariable dar. Die Anfangswerte
sind wie angegeben durch das Argument
definiert. Zu beachten ist, dass für
das vollständige elliptische Integral I. Art ins Unendliche läuft. Deshalb
kann
nicht berechnet werden. Dies stellt jedoch kein Problem dar, da dieser Wert
exakt zu
bekannt ist. Bei einer Implementierung bedarf es also einer Fallunterscheidung.
Die Parameter-Konvention
lässt sich ebenfalls mit dem AGM-Algorithmus berechnen. Es bedarf ausschließlich
der Substitution
.
In der Praxis zeigt sich, dass bei Verwendung von double-precision
(
dezimalen
Nachkommastellen) eine Wahl von
Rekursionsschritten die besten Ergebnisse liefert. Bei
sinkt die Genauigkeit aufgrund von Rundungsfehlern.
Diese geringe Anzahl an Rekursionsschritten zeigt die Effizienz des
AGM-Algorithmus.
| Anfangswerte | Rekursionsgleichungen | Elliptische Integrale |
|---|---|---|
Durch Substitution gemäß
findet sich weiterhin der sogenannte Quartic-AGM-Algorithmus, dessen
Iterationsvorschrift in der nachfolgenden Tabelle dargestellt ist. Die
Bezeichnung „Quartic“ bezieht sich auf die Konvergenz
des Algorithmus. Die Konvergenzordnung des Algorithmus in der oberen Tabelle ist
quadratisch.
| Anfangswerte | Rekursionsgleichungen | Elliptische Integrale |
|---|---|---|
Spezielle Eigenschaften und Identitäten
Hier sind ,
und
wieder die komplementären
Größen.
Spezielle Funktions-Werte
Dabei bezeichnet
die Lemniskatische
Konstante.
Spezielle Identitäten
Hierbei löst der Jacobische Sinus-Amplitudinis-Ausdruck
für x die Gleichung
auf.
Insgesamt gilt für alle Werte n ∈ ℕ und 0 ≤ k ≤ 1 folgende Formel:
Hierbei ist sn der Sinus Amplitudinis und dn das Delta amplitudinis.
Ableitungen
Die vollständigen elliptischen Integrale erster und zweiter Art werden so abgeleitet:
Beweis für die Ableitung des elliptischen Integrals erster Art:
Beweis für die Ableitung des elliptischen Integrals zweiter Art:
Stammfunktionen
Ursprungsstammfunktion für das vollständige elliptische Integral erster Art:
Beispiel:
Ursprungsstammfunktion für das vollständige elliptische Integral zweiter Art:
Beispiel:
Dabei ist G die Catalansche Konstante und mit Ti₂(x) wird das Arkustangensintegral zum Ausdruck gebracht.
Umkehrfunktionen
Umkehrfunktionen oder algebraische Funktionen von Umkehrfunktionen der elliptischen Integrale heißen elliptische Funktionen. Sie sind mit den trigonometrischen Funktionen verwandt.
Unvollständige elliptische Integrale
Definition der unvollständigen elliptischen Integrale
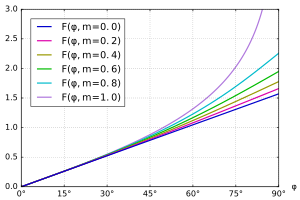
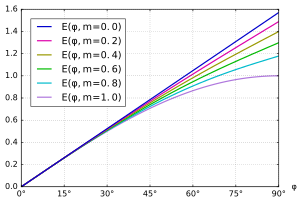
In der nachfolgenden Tabelle sind die Definitionen der unvollständigen
elliptischen Integrale in Jacobi-Form und in Legendre-Normalform angegeben. Die
Jacobi-Form lässt sich mit der Substitution
in die Legendre-Normalform überführen. Die unvollständigen elliptischen
Integrale besitzen im Vergleich zu den vollständigen elliptischen Integralen
einen zusätzlichen Freiheitsgrad, welcher der oberen Integrationsgrenze
entspricht. Somit stellen die vollständigen elliptischen Integrale einen
Spezialfall der Unvollständigen dar. In den Funktions-Bibliotheken von Matlab, Wolfram-Alpha, Mathematica, Python (SciPy) und GNU
Octave ist der Parameter
und die Legendre-Normalform in Verwendung.
| Konvention mit Parameter |
Konvention mit Parameter | |
|---|---|---|
| I. Art: Jacobi-Form | ||
| I. Art: Legendre-Normalform | ||
| II. Art: Jacobi-Form | ||
| II. Art: Legendre-Normalform | ||
| III. Art: Jacobi-Form | ||
| III. Art: Legendre-Normalform |
Additionstheoreme
Mit folgenden Theoremen können die unvollständigen elliptischen Integrale additiv verknüpft werden. Die Legendre-Normalform wird zur Darstellung verwendet.
Elliptische Integrale erster Art:
Elliptische Integrale zweiter Art:
Mit folgendem Theorem können arithmetische Mittlungen durchgeführt werden:
Modultransformation
Mit folgenden Formeln wird der Modul transformiert:
Für alle Werte n ∈ ℕ und 0 ≤ k ≤ 1 gilt folgende Formel:
Unvollständige elliptische Integrale als Stammfunktionen für algebraische Wurzelfunktionen
Mit dieser Formel lassen sich die Kehrwerte der Quadratwurzeln von Polynomen vierten Grades integrieren:
Hierbei müssen die Werte ,
,
und
alle vier positiv sein.
Beispiel:
Im Gegensatz dazu sind uneigentliche Integrale von Minus Unendlich bis Plus Unendlich von den Kehrwerten der Quadratwurzeln aus nullstellenfreien quartischen Polynomen immer als vollständige elliptische Integrale erster Art darstellbar. Beispielsweise gilt:
Alternative Darstellungen
Symmetrische Carlson-Formen
Die symmetrischen Carlson-Formen sind eine alternative Menge an Funktionen, durch die die klassischen elliptischen Integrale ausgedrückt werden können. Die moderneren Carlson-Formen wurden erst in den 1960er Jahren erfunden, während die Legendre-Formen bereits 1825 formuliert worden waren. Die Carlson-Formen bieten einige Vorteile gegenüber den klassischen elliptischen Integralen.
Unvollständige elliptische Integrale
Unvollständige elliptische Integrale können mit Hilfe der symmetrischen
Carlson-Formen ,
und
ausgerückt werden:
(für
und
)
Vollständige elliptische Integrale
Vollständige elliptischen Integrale erhält man durch Einsetzen von φ = π/2:
Bulirsch-Integrale
Eine alternative Darstellung der unvollständigen elliptischen Integrale sind die Bulirsch-Integrale
.
Diese sind äquivalent zu den Legendre-Normalformen:
Eine verallgemeinerte Version der vollständigen elliptischen Integrale ist das Bulirsch-Integral
Es gilt
Die Funktion cel hat den Vorteil, dass bestimmte in der Praxis vorkommende Kombinationen der normalen elliptischen Integrale als gemeinsame Funktion dargestellt werden können, und damit numerische Instabilitäten und undefinierte Wertebereiche vermieden werden können.
Numerische Auswertung
Die elliptischen Integrale können mit Hilfe des oben genannten arithmetisch-geometrischen Mittelwertes (AGM) effizient berechnet werden. Sie können auch zur Auswertung in die symmetrische Carlson-Form überführt werden. Zur numerischen Auswertung der Carlson-Formen existieren zum AGM ähnliche Algorithmen. Eine Annäherung mit Hilfe von gebrochenrationalen Funktionen höherer Ordnung ist auch möglich. Eine direkte numerische Quadratur z.B. mit dem tanh-sinh-Verfahren ist ebenfalls möglich.
Bezug zur Gammafunktion
Für alle n ∈ ℕ gilt folgender Zusammenhang zwischen der Gammafunktion und den elliptischen Integralen:
Bei der Berechnung des abgebildeten Integrals für die Werte n = 3, 4, 6 und 8 erhält man folgende Resultate:
Mit der Berechnung dieser Integrale und der Anwendung der Eulerschen Formel des Ergänzungssatzes lassen sich die Gamma-Funktionswerte ermitteln.
Anwendungsbeispiele
Umfang einer Ellipse
Eine klassische Anwendung ist die Berechnung des Umfangs
einer Ellipse. Im Folgenden ist eine
Ellipsen-Parameterform
mit den Halbachsen
,
angegeben. Das Ergebnis stellt sich mit dem vollständigen elliptischen Integral
II. Art dar. Hierbei ist die Parameter-Konvention
verwendet.
Die Äquivalenz der letzten beiden Ausdrücke ist ersichtlich, wenn vorher
statt
ausgeklammert wird. Im letzten Ausdruck ist
für
.
Die zugehörige Anwendung des unvollständigen elliptischen Integrals II. Art
ergibt sich, indem die obere Integrationsgrenze als Variable
wie im Folgenden angesetzt wird. Damit ergibt sich die Bogenlänge
der Ellipse in Abhängigkeit vom Parameter
.
Umfang und Flächeninhalt einer Cassinischen Kurve
Die Cassinischen Kurven gehorchen für den Fall a < c folgender Relation für kartesische Koordinaten:
Dabei ist a die Brennweite und c ist der Abstand zwischen Brennpunkt und Schnittstelle von Graph und Ordinatenachse.
Für den Umfang der Cassinischen Kurve gilt:
Für den Flächeninhalt der Cassinischen Kurve gilt:
Mathematisches Pendel
Eine klassische Anwendung der elliptischen Integrale ist die exakte Bewegung eines Pendels, bei welcher die Schwingungsdauer bei gegebenem Maximalauslenkungswinkel und gegebener Fadenlänge auf folgende Weise berechnet werden kann:
Dabei ist g ≈ 9,81 m/s² die Fallbeschleunigung der Erde.
Elektrisches Skalarpotential einer homogenen, kontinuierlichen, ringförmigen Ladungsverteilung
Eine klassische Problemstellung aus der Elektrostatik
ist die Berechnung des elektrischen Skalarpotentials
bei gegebener räumlicher Ladungsverteilung.
Bei einer homogenen, kontinuierlichen, ringförmigen Ladungsverteilung lässt sich
das elektrische Skalarpotential mit Hilfe des vollständigen elliptischen
Integrals 1. Art beschreiben. Das Ergebnis ist hier mit der
Parameter-Konvention
mit
angegeben. In der angegebenen Lösung repräsentiert
die elektrische Gesamtladung,
den Radius des Ringes und
die Vakuum-Permittivität.
Weiterhin ist das Skalarpotential mit den Zylinderkoordinaten
angegeben. Da keine Abhängigkeit bezüglich der Azimut-Koordinate
besteht, ist ersichtlich, dass es sich um eine zylindersymmetrische
Problemstellung handelt.
Elektrisches Skalarpotential einer homogenen, kontinuierlichen, ringförmigen Dipolverteilung
Neben der einfachen Ladungsverteilung besteht ebenfalls die Möglichkeit, eine
ringförmige Verteilung axial ausgerichteter Dipole
zu betrachten. Die Lösung des elektrischen Skalarpotentials ist im Folgenden
angegeben. Dabei repräsentiert
die
-Komponente
des elektrischen
Dipolmoments,
den Radius des Ringes und
die Vakuum-Permittivität. Das Ergebnis ist hier mit der Parameter-Konvention
mit
angegeben.
Magnetisches Vektorpotential eines ringförmigen stromdurchflossenen Leiters
Ein Beispiel aus der Magnetostatik
stationärer Ströme stellt die Berechnung des Magnetfeldes eines stromdurchflossenen
Ringleiters dar. Es bietet sich die Berechnung des
magnetischen
Vektorpotentials
an, aus dem sich in weiterer Betrachtung mit Hilfe der Rotation
die magnetische
Flussdichte bestimmen lässt. Hier repräsentiert
die elektrische
Stromstärke,
den Radius des Ringleiters und
die Vakuum-Permeabilität.
Weiterhin ist das magnetische Vektorpotential mit den Zylinderkoordinaten
und mit dem Einheits-Basisvektor
in azimutaler Richtung angegeben. Die Lösung stellt sich durch eine Kombination
von vollständigem elliptischen Integral 1. und 2. Art dar. Das Ergebnis ist
hier mit der Parameter-Konvention
mit
angegeben. Zur numerischen Auswertung der angegebenen Funktion eignet sich
besonders das weiter oben angegebene Bulirsch-Integral
.
Der Vorteil ist eine höhere numerische Stabilität in der Umgebung
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.09. 2022