
Ladungsdichte
| |||||||||||||||||||||||
| |||||||||||||||||||||||
| |||||||||||||||||||||||
Die elektrische Ladungsdichte ist eine physikalische Größe aus der Elektrodynamik, die eine Ladungsverteilung beschreibt. Da es sowohl positive als auch negative Ladungen gibt, sind für die Ladungsdichte ebenfalls sowohl positive als auch negative Werte möglich.
Da Ladungen auch an Oberflächen oder etwa entlang eines dünnen Drahtes verteilt sein können, kann die Ladungsdichte durch folgende Größen beschrieben werden:
- die Ladung pro Volumen (Raumladungsdichte), übliches Symbol ρ (rho)
- die Ladung pro Fläche (Oberflächenladungsdichte), übliches Symbol σ (sigma)
- die Ladung pro Länge (Linienladungsdichte), übliches Symbol λ (lambda).
Begrenzung der Oberflächenladungsdichte
Die erreichbare Oberflächenladungsdichte wird durch Koronaentladung in die umgebende Luft begrenzt, wenn die maximale Feldstärke von etwa 105 V/m überschritten wird:
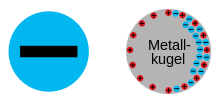
Damit trägt jeder negativ geladene Quadratzentimeter die Überschussladung 1,8·10−10 As, was 1,1·109 frei beweglichen Elektronen entspricht. Etwa eine Million Mal mehr Elektronen sind an die Atomrümpfe der Metalloberfläche gebunden (Siehe auch Influenz#Anzahl der beteiligten Elektronen).
Ähnliche Größen
Eine mit der Oberflächenladungsdichte σ korrespondierende Größe ist die
elektrische
Flussdichte
(auch elektrische Erregung, dielektrische Verschiebung oder Verschiebungsdichte
genannt), ein senkrecht auf der betreffenden Fläche stehender Vektor. Dagegen ist σ ein
Skalar
(und unter bestimmten Umständen gleich dem Betrag
).
Nicht mit der Ladungsdichte zu verwechseln sind außerdem die Ladungsträgerdichte, also die Anzahl der Protonen, Elektronen usw. pro Raum-, Flächen- oder Längeneinheit sowie die in der Dichtefunktionaltheorie berechnete Elektronendichte.
Definition
Die Definition der Raumladungsdichte ähnelt der Massendichte:
,
wobei Q die elektrische Ladung und V das Volumen ist.
Bei der Flächen- und der Linienladungsdichte wird entsprechend
nach der Fläche
bzw. nach der Länge
abgeleitet:
Flächen- und Linienladungsdichte können mit Hilfe der Delta-Distribution auch als eine Raumladungsdichte ausgedrückt werden. So kann die Raumladungsdichte einer Oberflächenladung in der X-Y-Ebene durch
beschrieben werden. Die Raumladungsdichte einer Linienladung auf der X-Achse kann ausgedrückt werden als
Diskrete Ladungsverteilung
Besteht die Ladung in einem Volumen aus
diskreten Ladungsträgern
(wie z.B. Elektronen), so kann die Ladungsdichte mit Hilfe der Delta-Distribution
ausgedrückt werden:
mit
- der Ladung
und
- dem Ort
des
-ten Ladungsträgers.
Tragen alle Ladungsträger die gleiche Ladung
(bei Elektronen gleich der negativen Elementarladung:
),
so kann man obige Formel mit Hilfe der Ladungsträgerdichte
vereinfachen:
Elektrisches Potential
Das elektrische Potential hängt gemäß der Poisson-Gleichung der Elektrostatik
nur von der Ladungsdichte ab. Hierbei bezeichnet
die Permittivität.
Point of zero charge
Der Point of zero charge (PZC) (dt. Punkt der Ladung null) ist erreicht, wenn die Ladungsdichte einer Oberfläche null beträgt. Dieses Konzept stammt aus der physikalischen Chemie und ist relevant für die Adsorption von Stoffen oder Partikeln an Oberflächen.
Für Partikel in Suspension ist der PZC der Punkt, an dem das Zeta-Potential null ist. Das kann beispielsweise für einen bestimmten pH-Wert der Fall sein. Abseits des PZC sind die Partikel geladen, stoßen einander daher elektrisch ab und neigen so weniger dazu, sich zu Flocken oder Aggregaten zusammen zu ballen. Die fehlende Ladung am PZC führt auch zu einer Verminderung der Löslichkeit/Hydratation in Wasser.
Die Kenntnis des PZC ist nützlich, um die Mobilität von gelösten Stoffen oder Partikeln einzuschätzen, was unter anderem für die Risikobewertung von Schadstoffen eine Rolle spielen kann.
Ein ähnliches Konzept ist der isoelektrische Punkt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.02. 2024