
Permittivität
| Physikalische Größe | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | dielektrische Leitfähigkeit oder Permittivität | |||||||||||||||
| Formelzeichen | ||||||||||||||||
| ||||||||||||||||
Die Permittivität ε (von lat. permittere: erlauben, überlassen, zulassen), auch dielektrische Leitfähigkeit, Dielektrizität, Dielektrizitätskonstante oder dielektrische Funktion genannt, gibt in der Elektrodynamik sowie der Elektrostatik die Polarisationsfähigkeit eines Materials durch elektrische Felder an.
Auch dem Vakuum ist eine Permittivität
zugewiesen, da sich auch im Vakuum elektrische Felder einstellen oder elektromagnetische
Felder ausbreiten können. Es handelt sich um eine Naturkonstante, nämlich
die elektrische
Feldkonstante .
Die Permittivität eines Stoffes wird dann als Vielfaches der Permittivität des
Vakuums angegeben:
Hierbei ist der Faktor
die stoffabhängige Permittivitätszahl (früher relative Permittivität). Sie hängt
jedoch nicht nur von der Art des Stoffes ab, sondern unter anderem auch von der
Frequenz der wirksamen Felder.
Erläuterung am Beispiel isolierender Stoffe
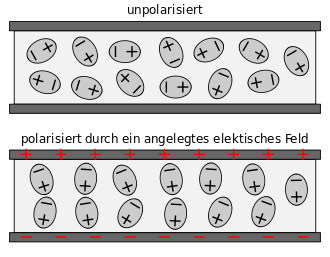
Als Permittivität bezeichnet man eine Materialeigenschaft elektrisch isolierender, polarer oder unpolarer Stoffe, die auch Dielektrika genannt werden. Die Eigenschaft wirkt sich aus, wenn der Stoff mit einem elektrischen Feld wechselwirkt, etwa wenn er sich in einem Kondensator befindet.
In einem mit Material gefüllten Kondensator orientieren sich die Ladungsträger
des Isolationsmaterials am
Vektor des elektrischen Feldes und erzeugen ein Polarisationsfeld,
das dem äußeren Feld entgegenwirkt und dieses schwächt. Dieses Phänomen der
Feldschwächung lässt sich bei Annahme eines gegebenen elektrischen
Erregungsfeldes ,
auch elektrische Flussdichte genannt, dadurch beschreiben, dass dem isolierenden
Material ein Faktor
zur elektrischen Feldkonstante
(Permittivität des Vakuums) zugewiesen wird. Im Vakuum als Referenzmaterial
eines Isolierstoffes gilt die relative Permittivität
Aus der äußeren elektrischen Erregung ergibt sich dann mit der Permittivität
das elektrische Feld
zu:
Bei konstanter elektrischer Erregung und steigenden Werten von
nimmt die elektrische Feldstärke ab. Auf diese Weise wird der feldschwächende
Effekt bei gleicher elektrischer Erregung erfasst, d.h. bei vorgegebener
elektrischer Flussdichte oder vorgegebener elektrischer Ladung.
Unter der Einwirkung einer an den Kondensatorplatten angelegten festen Spannung U
und dem elektrischen Feld
(Plattenabstand d) ergibt sich mit der Permittivität als Proportionalitätsfaktor
die elektrische Erregung zu:
Die elektrische
Suszeptibilität
ist mit der relativen Permittivität verknüpft über
Die Suszeptibilität ist dabei ein Maß für die Dichte der im Isolationsmaterial gebundenen Ladungsträger, bezogen auf die Dichte freier Ladungsträger.
Gemäß der Poisson-Gleichung
der Elektrostatik kann die Permittivität außerdem als Proportionalitätsfaktor
zwischen der Raumladungsdichte
und der zweiten partiellen
Ableitung des Potentialfelds
angesehen werden:
Permittivität des Vakuums
Die Permittivität des Vakuums
ist eine Naturkonstante.
Im Vakuum besteht zwischen der magnetischen
Feldkonstanten
,
der Permittivität
des Vakuums und der Vakuumlichtgeschwindigkeit
folgender Zusammenhang:
Die Einheit der Permittivität kann ausgedrückt werden als:
Da die elektrische Polarisierbarkeit
von Luft gering ist, kann die Permittivität der Luft
(εr ≈ 1,00059) häufig in ausreichender Genauigkeit
durch
genähert werden. Dies ist insbesondere bei Radar
und in der Funktechnik
der Fall.
Zahlenwert und Einheit
Neben dem Coulomb-Gesetz,
dem Ampèreschen
Gesetz und dem Faradayschen Induktionsgesetz
stellt der Zusammenhang zwischen μ0,
und c eine weitere Verknüpfung elektromagnetischer und mechanischer
Einheiten dar, die bei der Wahl eines elektromagnetischen
Einheitensystems zu berücksichtigen ist.
Abhängig vom verwendeten Einheitensystem verändert sich dabei die Darstellung
der Permittivität
analog zur Darstellung von
.
Die Verhältnisse im SI sind oben angegeben. In Einheitensystemen, die die
elektromagnetischen Größen explizit auf mechanische Basisgrößen zurückführen,
namentlich den verschiedenen Varianten des CGS-Einheitensystems,
wird
als Größe
der Dimension Zahl gewählt:
(Heaviside-Lorentz-Einheitensystem),
(elektrostatisches, elektromagnetisches oder Gaußsches Einheitensystem).
Relative Permittivität
Die relative Permittivität
eines Mediums (Bezeichnung nach Norm DKE-IEV 121-12-13),
auch Permittivitäts- oder Dielektrizitätszahl genannt, ist das dimensionslose
Verhältnis seiner Permittivität
zur Permittivität
des Vakuums:
Für gasförmige, flüssige und feste Materie ist .
Allerdings gibt es in anderen Materiezuständen, z.B. im Plasma, auch Werte
.
Die relative Permittivität ist ein Maß für die feldschwächenden Effekte der
dielektrischen
Polarisation des Mediums. In der englischsprachigen Literatur und daher auch
in englischsprachig geprägten Fachbereichen wie der Halbleitertechnik
wird die relative Permittivität auch mit
(kappa) oder
– wie etwa bei den high-k-Dielektrika
bzw. bei den low-k-Dielektrika –
mit k bezeichnet.
Als Synonym für die (relative) Permittivität ist die frühere Bezeichnung
(relative) Dielektrizitätskonstante weiterhin in Gebrauch. Die
Bezeichnung als Konstante ist unangemessen, da
im Allgemeinen eine Funktion mehrerer Parameter ist, insbesondere der Frequenz und der Temperatur;
außerdem hängt sie auch vom Magnetfeld
und vom äußeren elektrischen Feld ab.
Nur für isotrope
Medien ist
eine skalare
Größe. In diesem einfachsten Fall gibt sie den Faktor an, um den die Spannung an
einem Kondensator sinkt, wenn man bei gleicher Geometrie ein zwischen den
Kondensatorelektroden angenommenes
Vakuum durch ein dielektrisches, nicht leitendes Material ersetzt. Im Versuch
lässt sich dies nachvollziehen, wenn ein Luftvolumen um die
Kondensatorelektroden z.B. durch eine dielektrische Flüssigkeit ersetzt
wird. Für einen Plattenkondensator genügt es, einen dielektrischen Gegenstand
zwischen die Elektroden zu schieben.
Richtungsabhängigkeit
Im Allgemeinen ist die relative Permittivität ein Tensor zweiter Stufe. So wird ihre Richtungsabhängigkeit widergespiegelt, die sich aus der kristallinen (oder anders geordneten) Struktur der Materie ergibt, z.B. für doppelbrechende Materialien, die u.a. bei Verzögerungsplatten angewendet werden. Die Tensoreigenschaft der Permittivität ist Grundlage der Kristalloptik.
Neben der „natürlichen“ Richtungsabhängigkeit können die Eigenschaften auch durch äußere Einwirkungen wie ein Magnetfeld (Magnetooptik) oder Druck eine ähnliche Richtungsabhängigkeit erfahren.
Frequenzabhängigkeit
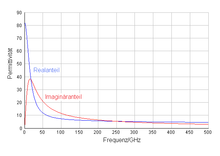
Der Realteil beschreibt Kapazität bzw. Brechungsindex, der Imaginärteil die Energieabsorption.
Die Frequenzabhängigkeit (Dispersion) der Permittivität in Materie kann über den Lorentz-Oszillator recht gut modelliert werden und ist z.B. bei Wasser sehr stark ausgeprägt, vgl. Abbildung.
Wie die elektrische Permittivität hängt auch der Brechungsindex
eines Materials von der Frequenz
ab, da er gemäß den Maxwell-Gleichungen
zur Permittivität in folgender Relation steht:
mit
- der magnetischen
Permeabilität
; für transparente Stoffe gilt
und damit
.
Hier sind
und μ bei der einschlägigen optischen Frequenz gemeint (Größenordnung
1015 Hz). Die optische
Dispersion ist ein Ausdruck dafür, dass
auch bei den Frequenzen sichtbaren
Lichts keine konstante Zahl ist.
In Tabellenwerken ist in der Regel der Zahlenwert bei niedrigen Frequenzen (Größenordnung 50 Hz bis 100 kHz) angegeben, bei denen molekulare Dipole dem äußeren Feld noch nahezu unverzögert folgen können.
Komplexwertige relative Permittivität
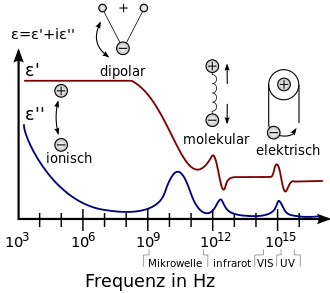
Genauso wie bei Gleichfeldern bilden sich in Dielektrika auch bei Wechselfeldern Polarisationsfelder, die aber der angelegten äußeren Feldgröße um einen gewissen Phasenwinkel nacheilen. D.h., die Orientierung der Ladungsträger im Dielektrikum bleibt in der Phase zeitlich hinter der Umpolarisierung des Wechselfeldes zurück.
Daher ist die relative Permittivität im Allgemeinen komplexwertig:
oder auch
Dabei können in Real- und Imaginärteil die Beiträge verschiedener Mechanismen im Material (z.B. Bandübergänge) angegeben und in ihrer Frequenzabhängigkeit addiert werden – eine detailliertere Darstellung findet sich unter elektrische Suszeptibilität.
Mit zunehmender Frequenz
wird der Effekt des Nacheilens stärker. Indem sie isolierende Materialien
schnell und wiederkehrend umpolarisieren, wandeln Wechselfelder hoher Frequenz elektromagnetische
Feldenergie in Wärmeenergie
um. Dieser Wärmeverlust
wird dielektrischer Verlust genannt und durch den Imaginärteil
bzw.
der komplexwertigen relativen Permittivität beschrieben.
Eine weitverbreitete Anwendung, die das Phänomen der dielektrischen Erwärmung ausnutzt, ist der Mikrowellenofen.
Bei dielektrischer Erwärmung beträgt die Verlustleistungsdichte, bezogen auf das Materialvolumen
mit der Kreisfrequenz
.
Siehe auch Dielektrischer
Verlustfaktor.
Die mit der dielektrischen Erwärmung verbundene Verlustleistung entspricht bei Integration über den Erwärmungszeitraum exakt der inneren Energie, die dem Materialvolumen mit elektromagnetischen Wellen zugeführt wurde, wie in der Thermodynamik beschrieben.
Bei noch höheren Frequenzen, mit denen Ladungsträger im Bändermodell eines Kristalls angeregt werden können, wird ebenfalls Energie absorbiert (dielektrische Absorption).
Feldstärkeabhängigkeit
Im Falle großer Feldstärken
wird der Zusammenhang zwischen elektrischem Feld und Flussdichte nichtlinear. Entweder fasst
man die Permittivität als feldstärkeabhängig auf
oder man führt neben
weitere Taylor-Koeffizienten
usw. ein, die die Feldstärkeabhängigkeit von
beschreiben:
Temperaturabhängigkeit
Temperaturabhängig ist beispielsweise die komplexwertige relative Permittivität von Wasser, deren Realteil bei einer Frequenz von 1 GHz und einer Temperatur von 20 °C einen Wert von etwa 80 annimmt, und bei 95 °C circa 52 beträgt. Die Abnahme der Permittivität bei steigender Temperatur hängt mit dem zunehmenden Grad der Unordnung der Ladungsträger bei einer Zunahme der inneren Energie zusammen. Molekular betrachtet nimmt die Polarisierbarkeit aufgrund der zunehmenden Eigenbewegung der Ladungsträger bei höherer innerer Energie ab; makroskopisch betrachtet sinkt somit die relative Permittivität bei Temperaturerhöhung.
Werte für ausgewählte Materialien
| Medium | Medium | |||
|---|---|---|---|---|
| Vakuum | exakt 1 | Luft | 1,00059 | |
| Aceton | 21,5 | |||
| Acrylglas | 3 | |||
| Acrylnitril-Butadien-Styrol (ABS) (30 °C) | 4,3 | Aluminiumoxid (Tonerde) | 9 | |
| Ammoniak (0 °C) | 1,007 | Bariumtitanat | 103…104 | |
| Benzol | 2,28 | Trockene Erde | 3,9 | |
| Feuchte Erde | 29 | Germanium | 16,6 | |
| Glas | 6…8 | Glycerin | 42,5 | |
| Glimmer | 5…8 | |||
| Gummi | 2,5…3 | Holz (darrtrocken) | 2…3,5 | |
| Kaliumchlorid | 4,94 | Methanol | 32,6 | |
| Petroleum | 2 | Polyethylen (PE) (90 °C) | 2,4 | |
| Polypropylen (PP) (90 °C) | 2,1 | Porzellan | 2…6 | |
| Propanol | 18,3 | Paraffin | 2,2 | |
| Papier | 1…4 | Polytetrafluorethylen (PTFE oder auch Teflon) |
2 | |
| Polyethylen, Polypropylen | 2,3 | Kabelpapier in Öl | 4,3 | |
| FR2, FR4 | 4,3…5,4 | Polystyrol-Schaum (Styropor ® BASF) |
1,03 | |
| Polystyrol | 2,5 | Polyvinylchlorid | 3…4 | |
| Porzellan | 5…6,5 | Schellack | 3…4 | |
| Tantalpentoxid | 27 | Wasser (20 °C, 0…3 GHz) | 80 | |
| Wasser (sichtbarer Bereich) | 1,77 | Wasser (0 °C, 0…1 GHz) | 88 | |
| Eis (0 bis −50 °C, Niederfrequenz) | ≈ 90…150 | Eis (über 100 kHz) | 3,2 |
Zusammenhang mit Absorption und Reflexion
Über die Kramers-Kronig-Relation kann der dispergierende Zusammenhang zwischen der komplexen Permittivität und den optischen Kenngrößen Brechungsindex und Absorptionskoeffizient k dargestellt werden:
Im Falle nichtmagnetischer Materialien ()
folgt nach einem Koeffizientenvergleich:
Für die Berechnung theoretischer Spektren von Reflexion und Absorption, die mit gemessenen Spektren verglichen und angepasst werden können, sind die Komponenten des komplexen Brechungsindizes direkt aus Real- und Imaginärteil der Permittivität zu bestimmen:
Ebenfalls kann u.a. der Reflexionsgrad R
berechnet werden für einen Strahl, der aus dem Vakuum (bzw. Luft) kommend
senkrecht an einer Grenzfläche
zu einem Medium mit Brechungsindex
reflektiert wird:
Literatur
- Heinrich Frohne: Einführung in die Elektrotechnik. Band 2: Heinrich Frohne, Erwin Ueckert: Elektrische und magnetische Felder. (= Teubner Studienskripten. Bd. 2: Elektrotechnik.). 4., durchgesehene Auflage. Teubner, Stuttgart 1983, ISBN 3-519-30002-8.
- Károly Simonyi: Theoretische Elektrotechnik. 10. Auflage. Barth Verlagsgesellschaft, Leipzig u.a. 1993, ISBN 3-335-00375-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.10. 2023