
Relaxation (Naturwissenschaft)
Relaxation bezeichnet im naturwissenschaftlichen Bereich den Übergang eines Systems über Relaxationsprozesse in seinen Grundzustand oder in einen Gleichgewichtszustand (häufig nach einer Anregung oder einer äußeren Störung).
Die Relaxationszeit (genauer Relaxationszeitkonstante[Anm. 1]) beschreibt die charakteristische Zeit[Anm. 2], in welcher sich ein System (meist exponentiell) dem stationären Zustand annähert. Anschaulich hat sich das System nach der Dauer einer Relaxationszeitkonstante merklich auf seinen Gleichgewichtszustand zubewegt; nach der Dauer von drei bis sechs Relaxationszeitkonstanten kann man gewöhnlich von einer weitgehend abgeschlossenen Relaxation ausgehen. Der Kehrwert der Relaxationszeitkonstante wird als Relaxationsrate bezeichnet.
Mathematische Beschreibung
Wenn die Relaxation einer Größe
vom Anfangswert
zum asymptotischen
Endwert
einem exponentiellen Gesetz folgt:
,
dann ist
die zugehörige Relaxationszeitkonstante
und
die Relaxationsrate.
Nach der Zeit
(Halbwertzeit)
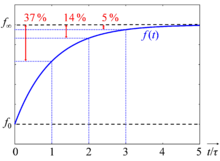
hat sich die Größe bis auf die Hälfte dem Endwert angenähert, nach
auf ca. 36,8 % (
),
nach
bis auf ca. 13,5 % und nach
bis auf ca. 5,0 %; d.h., das System ist zu diesem Zeitpunkt zu ca.
95 % (also fast vollständig) relaxiert.
Im Falle komplizierterer (zum Beispiel gestreckt-exponentieller) Zeitabhängigkeiten kann man die Relaxationszeit definieren als
.
Beispiele
- Die Wärmeübertragung
mit der thermischen Relaxationszeit
; diese beschreibt, wie schnell sich die Temperatur eines Körpers an die veränderte Umgebungstemperatur anpasst (Newtonsches Abkühlungsgesetz). Hier ist
die Masse des Körpers,
die spezifische Wärmekapazität,
der Wärmeübergangskoeffizient und
die Grenzfläche.
- Die Magnetisierungsrelaxation
bei der Kernspinresonanz
(NMR) oder Elektronenspinresonanz
(ESR) mit den Relaxationszeiten
und
der longitudinalen und transversalen Magnetisierung.
- Der Lade- und Entladeprozess des Kondensators
eines RC-Glieds in der Elektronik mit der
Relaxationszeit
, siehe Zeitkonstante.
- Die Violent Relaxation der kinetischen Energie eines Sterngases oder Galaxienhaufens, so dass sich ein thermisches Gleichgewicht einstellt.
- Der zeitliche Ablauf einer chemischen Reaktion gemessen mit der Relaxationsmethode, siehe auch Kinetik (Chemie).
- Die zeitliche Abnahme der mechanischen Spannung bei konstanter Dehnung in der Festigkeitslehre.
- Bewegt sich ein Ion (Zentralion) einer Salzlösung im elektrischen Feld mitsamt seiner Ionenwolke von „Gegenionen“, so muss es in Bewegungsrichtung die Ionenwolke jeweils neu aufbauen und "hinter sich" wieder abbauen. Dieser Vorgang benötigt Zeit, die sogenannte Relaxationszeit. Dadurch wird das Ion von seiner Ionenwolke gebremst. Dieser Effekt wird als Relaxationseffekt oder Asymmetrieeffekt bezeichnet und verringert die elektrolytische Leitfähigkeit der Lösung. Bei hohen Frequenzen (oberhalb 1 MHz) verschwindet dieser Effekt. Letzteres wird als Dispersionseffekt oder Debye-Falkenhagen-Effekt bezeichnet.
- bei Gasentladungsröhren: Ionisierungszeit (Zündverzugszeit/Einschaltzeit/Aufbauzeit) und Entionisierungszeit (Erholzeit/Abschaltzeit) sind Relaxationszeiten. Auftreten z.B. bei: Glimmlampen, Gasableitern, Sperröhren, Kaltkathoden-Relaisröhren, Thyratrons, Ignitrons Gasgleichrichtern/Quecksilberdampfgleichrichtern und Zählrohren, sowie Hochdrucklampen und Höchstdrucklampen und Blitzröhren. Die übliche Ionisierungszeit liegt bei Kaltkathodenröhren mit/ohne Hilfsentladung unter 0,1 ms/deutlich über 0,1 ms. Die Entionisierungszeit liegt zwischen 0,1 und 10 ms, wenn zuvor hohe Ströme geflossen sind auch höher. Wegen der höheren Entionisierungszeit (Abschaltzeit) bestimmt diese praktisch meist allein die Grenzfrequenz einer Gasentladungsröhre. Die Grenzfrequenz von Kaltkathodenröhren liegt meist im Bereich 0,5 bis 2 kHz. Bei gasgefüllten Zählrohren für Radioaktivität bestimmt die Entionisierungszeit die maximal mögliche Zählfrequenz.
- bei Halbleiterbauelementen:
- bei Dioden: Sperrverzögerungszeit
(Rückwärtserholzeit)
und die damit verknüpfte maximale Betriebsgrenzfrequenz
- bei Thyristoren und Triacs: Zündverzugszeit
bzw. die identische Einschaltzeit
; sowie die Auschaltzeit
oder die identische Freiwerdezeit
- bei Bipolar-Transistoren:
Einschaltzeit
, die sich additiv aus Verzögerungszeit
und Anstiegszeit
zusammensetzt; sowie die Auschaltzeit
, die sich additiv aus Speicherzeit
und Abfallzeit
zusammensetzt
- bei Dioden: Sperrverzögerungszeit
(Rückwärtserholzeit)
- Zeitkonstante
in der Regelungstechnik, insbesondere für reale PID-Regler mit Verzögerungsglied 1. Ordnung
Weitere Bedeutungen
In der Festkörperphysik und Oberflächenchemie wird das Vorliegen von veränderten Atomabständen an oder nahe der Festkörperoberfläche als (Oberflächen-)Relaxation bezeichnet. Hierbei handelt es sich nicht um einen dynamischen Relaxationsprozess im Sinne der oben gegebenen Beschreibung.
Anmerkungen
- ↑ Die Unterscheidung von „Relaxationszeit“ und „Relaxationszeitkonstante“ ist sinnvoll, da in Experimenten zur Beobachtung oder Quantifizierung der Relaxation auch die frei wählbare Dauer, während der man ein System relaxieren lässt, als „Relaxationszeit“ bezeichnet wird.
- ↑ Da ein System, das seinem Gleichgewichtswert asymptotisch (z.B. exponentiell) zustrebt, unendlich lange bis zur vollständigen Gleichgewichtseinstellung benötigt, wird nicht diese Dauer als Relaxationszeit definiert, sondern die Zeitspanne, nach deren Verstreichen ein gewisser prozentualer Wert des Gleichgewichtswertes erreicht wird.
Literatur
- Ernst Schmutzer: Grundlagen der Theoretischen Physik. 3. überarbeitete Auflage. Wiley-VCH-Verlag, Weinheim 2005, ISBN 3-527-40555-0.
- Klaus Dransfeld, Paul Kienle, Georg Michael Kalvius: Physik I. Mechanik und Wärme. 10., überarbeitete und erweiterte Auflage. Oldenbourg Wissenschaftsverlag, München 2005, ISBN 3-486-57810-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.01. 2025