Debye-Hückel-Theorie
Die Debye-Hückel-Theorie (nach Peter Debye und Erich Hückel) beschreibt in der Elektrochemie die elektrostatischen Wechselwirkungen von Ionen in Elektrolytlösungen.
Diese Coulombschen Anziehungs- und Abstoßungskräfte führen zu einer
Abweichung der Aktivität
(wirksame Konzentration, früher „aktive
Masse“) der Ionensorte
von ihrer molaren
Konzentration
gemäß
.
Die Debye-Hückel-Theorie liefert Gleichungen, mit denen der individuelle dimensionslose
Aktivitätskoeffizient
(teilweise auch als
geschrieben) in Abhängigkeit von Konzentration, Temperatur und Dielektrizitätskonstante
des Lösungsmittels berechnet werden kann.
Modellvorstellung
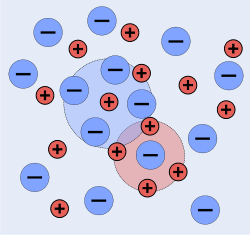
Entgegengesetzt geladene Ionen ziehen sich an, gleichnamig geladene Ionen stoßen sich ab. Aus diesen Gründen sind Ionen in einer Lösung nicht willkürlich verteilt, sondern besitzen eine gewisse Nahordnung, in der Anionen eher in der Nähe von Kationen zu finden sind und umgekehrt (Abb.). Elektroneutralität der Lösung ist dabei gewahrt.
Im Gegensatz zum Ionengitter können sich Ionen in Lösung nicht vollständig regelmäßig anordnen, weil Lösungsmittelmoleküle als Dielektrikum die Coulombschen Wechselwirkungen abschwächen, worauf die thermische Bewegung zu einer stärkeren Verteilung der Ionen führt. Im zeitlichen Mittel befindet sich aber jedes Ion im Zentrum einer Wolke aus entgegengesetzt geladenen Ionen (in der Abb. durch Kreise angedeutet). Diese Ionenwolken schirmen die Ladung des Zentralions ab, was der Grund für die Einführung der Aktivität als „wirksame Konzentration“ bei Ionen ist.
Die Theorie
Ausgehend von der o.g. Modellvorstellung haben P. Debye und E. Hückel durch Kombination der Poisson-Gleichung mit der Boltzmann-Statistik zur Beschreibung der Ionenverteilung einige häufig benutzte Gleichungen abgeleitet.
Aktivitätskoeffizient f der Ionensorte i
mit
- Ladungszahl
- Elementarladung
- Permittivität
des Lösungsmittels (
)
- Boltzmannkonstante
- absolute
Temperatur
- Radius
(des Zentralions, nicht der umgebenden Ionenwolke)
- Abkürzung
in
- Avogadro-Konstante
- Faraday-Konstante
- Universelle
Gaskonstante
- Ionenstärke
in
- Konzentration
in der Lösung
- Konzentration
- Avogadro-Konstante
Obige Gleichung wird oft als erweitertes Debye-Hückel-Grenzgesetz bezeichnet, das sich in seiner Schreibweise wie nachstehend gezeigt zusammenfassen lässt:
| Temperatur in °C |
A in |
B in |
|---|---|---|
| 0 | 0,4883 | 0,3241 · 1010 |
| 15 | 0,5002 | 0,3267 · 1010 |
| 20 | 0,5046 | 0,3276 · 1010 |
| 25 | 0,5092 | 0,3286 · 1010 |
| 30 | 0,5141 | 0,3297 · 1010 |
| 40 | 0,5241 | 0,3318 · 1010 |
| 50 | 0,5351 | 0,3341 · 1010 |
| 60 | 0,5471 | 0,3366 · 1010 |
| 80 | 0,5739 | 0,3420 · 1010 |
mit
in
in
Der Gültigkeitsbereich liegt bei ca.
Radius der Ionenwolke
Das Reziproke
von
lässt sich als Radius der Ionenwolke interpretieren:
Diesen Radius nennt man auch Abschirm- oder Debye-Länge.
Debye-Hückel-Grenzgesetz
Für Ionenwolken, die wesentlich größer sind als das umschlossene Ion (in der
Regel sind das stark verdünnte
Lösungen mit ):
ergibt sich die für praktische Belange am häufigsten zitierte Gleichung:
Darin ist
zu setzen, wenn Wasser bei 25 °C als Lösungsmittel verwendet wird. Für
andere Temperaturen und/oder Lösungsmittel muss es nach der oben angegebenen
Gleichung berechnet werden (vgl. auch Tabelle).
Mittlerer Aktivitätskoeffizient
Individuelle Aktivitätskoeffizienten (bzw. -aktivitäten) können zwar berechnet, aber aufgrund der Elektroneutralitätsbedingung nicht gemessen werden. Für den messbaren mittleren Aktivitätskoeffizienten eines Elektrolyten gilt
Näheres siehe Aktivität.
Der Aktivitätskoeffizient wird beispielsweise beim Massenwirkungsgesetz, zur Bestimmung des Löslichkeitsproduktes und der Siedepunktserhöhung verwendet.
Debye-Hückel-Onsager-Gesetz zur Leitfähigkeit von Ionen
Das Debye-Hückel-Gesetz wurde 1927 von Onsager zur Bestimmung der molaren
Leitfähigkeit
verwendet: nach Debye-Hückel bremst die gegensätzlich geladene Ionenwolke die
Wanderungsgeschwindigkeit
ihres Zentralions, die bisher nach dem
Ostwaldschen
Verdünnungsgesetz und dem Kohlrauschschen
Quadratwurzelgesetz berechnet wurde. Auf die Stärke der Abbremsung hat die
Viskosität des
Lösungsmittels gewichtigen Einfluss. Durch die Debye-Hückel-Onsager-Theorie
wurde verbessert, dass die Ionenbeweglichkeit und die molare Leitfähigkeit nun
von der Konzentration
abhängen.
So können für verdünnte Lösungen (≤ 0,01 Mol/Liter) in Wasser bei 25 °C folgende Beziehungen aufgestellt werden:
- für (starke) 1,1-Elektrolyte:
- für 2,1 -Elektrolyte (z.B. Na2SO4):
- für 1,2 -Elektrolyte (z.B. MgCl2):
- für 2,2-Elektrolyte:
- für 3,1-Elektrolyte:
Weitere Verbesserungen der Theorie kamen durch die mathematische Beschreibungen von Doppel- und Tripelionen unter E. Wickie und Manfred Eigen. Mit diesen Modellen wurde das Debye-Hückel-Onsager-Gesetz auf höher konzentrierte Lösungen (≤ 1 Mol/Liter) ausgedehnt.
Bei einer gerichteten Bewegung in einem elektrischen Feld tritt auch eine Störung der Symmetrie der Ionenwolke ein. Die durch Bewegung des Zentralions entstehende Unsymmetrie mit Bremswirkung nennt man Relaxations- oder Asymmetrie- oder Wien-Effekt und die Zeitperiode, bis sich die Ionen wieder neu ordnen, Relaxationszeit. Bei hohen Frequenzen (über 1 MHz), die der Relaxationszeit entsprechen, entfällt die elektrostatische Bremswirkung der Ionenbewegung. Die molare Leitfähigkeit oder Äquivalentleitfähigkeit der Ionen erreicht dann ihr Maximum (mindestens die Grenzleitfähigkeit) – auch bei höheren Konzentrationen.
Laut dem Buch chimica Band II S. 148 (Gl. 8.56), gilt nach Debye-Hückel-Onsager allgemein für alle Äquivalentleitfähigkeiten:
Darin sind
und
Konstanten, die nur von Temperatur, Dielektrizitätskonstante
des Lösemittels und den Wertigkeiten
der Ionen abhängen.
ist die Ionenstärke
(quadratisch nach den Wertigkeiten gewichtete mittlere Konzentration).
Da die molaren Leitfähigkeiten das Produkt von Äquivalentleitfähigkeiten und Wertigkeit/Ladungsaustauschzahl des Ions/der Ionen sind, können die Gleichungen für molare Leitfähigkeiten in Gleichungen für Äquivalentleitfähigkeiten umgeformt werden(es ergeben sich dann andere Konstanten im Modell).
Empirische Erweiterungen für konzentriertere Lösungen
Aufbauend auf dem erweiterten Debye-Hückel-Grenzgesetz wurden durch Anfügen weiterer Terme Beziehungen erhalten, die auch für konzentriertere Lösungen verwendet werden können, insbesondere die Gleichungen von Guggenheim und Davies.
Literatur
- Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.06. 2025