Zeitkonstante
Die Zeitkonstante (griech.
(tau) oder
)
ist eine charakteristische Größe eines linearen dynamischen
Systems, das durch eine gewöhnliche
Differentialgleichung oder durch eine zugehörige Übertragungsfunktion
beschrieben wird. Sie hat die Dimension einer Zeit; ihre Maßeinheit ist meist
die Sekunde.
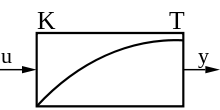
nach einem Eingangssprung.
Ein dynamisches System ist eine Funktionseinheit zur Verarbeitung und
Übertragung von Signalen; die Systemeingangsgröße
ist als Ursache und die Systemausgangsgröße
als zeitliche Auswirkung definiert. Typische Eingangssignale zur Prüfung des
Systemverhaltens sind die Impulsfunktion,
Sprungfunktion
und Anstiegsfunktion.
In der Elektrotechnik ist das Zeitverhalten eines Verzögerungsgliedes
1. Ordnung (z.B. eines RC-Glied-Tiefpasses)
mit einer Sprungantwort mit exponentiellem asymptotischem Verlauf allgemein
bekannt. Dabei bestimmt die Zeitkonstante
den zeitlichen Verlauf. Nach Ablauf einer Zeit von ca. 3 Zeitkonstanten hat das
Ausgangssignal ca. 95 % der Größe des Eingangssignals erreicht, wenn die
Systemverstärkung
ist.
Grundsätzlich hängt der zeitliche Verlauf des Ausgangssignals eines Übertragungssystems
beliebiger Ordnung von der Art des Übertragungssystems und des Eingangssignals
ab und bezieht sich nicht nur auf Zeitverzögerungsglieder (-Glieder).
Der Begriff Zeitkonstante ergibt sich bei der Beschreibung eines linearen
dynamischen Systems durch eine gewöhnliche
Differentialgleichung mit konstanten Koeffizienten. Zur leichteren
Berechnung des zeitabhängigen Systemverhaltens wird die systembeschreibende
Differentialgleichung der Laplace-Transformation
unterzogen und daraus das Signalverhältnis als Übertragungsfunktion
gebildet.
Die Übertragungsfunktion in der Zeitkonstantendarstellung entsteht wie folgt:
- Laplace-Transformation der gewöhnlichen Differentialgleichung höherer Ordnung,
- Bildung der Übertragungsfunktion
.
- Die Polstellen
und Nullstellen
der Übertragungsfunktion sind die wichtigsten Kenngrößen des Systemverhaltens.
- Faktorisierung der Polynome in die Pol-Nullstellendarstellung:
- Umrechnung der Pol-Nullstellendarstellung durch Zahlenwerte der Pole und Nullstellen in die Zeitkonstantendarstellung,
- Die Werte der Pole und Nullstellen eines Linearfaktors können drei Formen annehmen: Null, negativ reell, negativ konjugiert komplex.
- Damit können im Zähler und Nenner der Übertragungsfunktion insgesamt
unterschiedliche Grundformen von Linearfaktoren und Faktoren 2. Ordnung mit unterschiedlichem Systemverhalten entstehen.
.
Die Zeitkonstante
entspricht dem Koeffizienten
vor der komplexen Laplace-Variable
.
Sie errechnen sich allgemein aus dem Reziprokwert
einer negativen reellen Polstelle
oder einer Nullstelle
des Nennerpolynoms oder
Zählerpolynoms der Übertragungsfunktion als:
bzw.
.
Bestimmung der Zeitkonstanten aus den Polynomen eines linearen dynamischen Übertragungssystems höherer Ordnung
Systembeschreibungen durch Übertragungsfunktionen
können entstehen durch:
- Laplace-Transformation der systembeschreibenden gewöhnlichen Differenzialgleichung zu einer Übertragungsfunktion,
- Komplexe Spannungsteiler aus einem rückwirkungsfreien Impedanzverhältnis, (Beispiel: RC-beschaltete Operationsverstärker),
- Systemidentifikation mittels Sprung- oder Impulsantwort.
Zur einfacheren Berechnung und zum leichteren Verständnis wird die
systembeschreibende gewöhnliche Differenzialgleichung einer
Laplace-Transformation unterzogen und ist damit algebraisch
berechenbar. Dabei wird nach dem Laplace-Differentiationssatz eine Ableitung 1.
Ordnung der Differenzialgleichung durch die Laplace-Variable
als komplexe
Frequenz ersetzt. Höhere Ableitungen n-ter Ordnung werden entsprechend der
Ordnungszahl
durch
ersetzt.
Beispiel einer gewöhnlichen Differentialgleichung höherer Ordnung eines
Übertragungssystems mit konstanten Koeffizienten
und
:
Diese allgemeine Form der Differentialgleichung wird einer Laplace-Transformation unterzogen:
.
Durch Anwendung des Laplace-Differentiationssatzes auf die
systembeschreibende gewöhnliche Differentialgleichung entsteht die
Übertragungsfunktion .
Mittels der Pol- und Nullstellenbestimmung des Zähler- und Nennerpolynoms
entsteht die faktorielle Darstellung (Linearfaktoren) der Übertragungsfunktion.
Die Übertragungsfunktion G(s) wird aus dem Verhältnis der Ausgangsgröße zur Eingangsgröße gebildet. Dabei dürfen keine Anfangswerte der inneren Energiespeicher (Zustandsraumdarstellung) des Systems bestehen.
Die Laplace-Variable
ist eine unabhängige Variable im komplexen Frequenzbereich (Bildbereich,
s-Bereich) mit
als Realteil und
als Imaginärteil. Sie erlaubt beliebige algebraische Operationen im s-Bereich,
ist aber nur ein Symbol für eine vollzogene Laplace-Transformation und enthält
keinen Zahlenwert. Exponenten von s entsprechen dem Grad der Ableitung der Differentiale.
Zur Bestimmung der elementaren Einzelsysteme
einer Übertragungsfunktion G(s) höherer Ordnung werden die Polynome des Zählers
und Nenners durch Nullstellenbestimmung faktorisiert.
Wenn Zahlenwerte der Koeffizienten vorliegen, können mit verschiedenen
Methoden die Pole und Nullstellen berechnet werden. Dazu eignet sich die
sogenannte pq-Formel
für Systeme 2. Ordnung. Fertige im Internet verfügbare Programme für Systeme bis
4. Ordnung können mit dem Aufruf: „Nullstellen (Lösungen) von Polynomen
bestimmen“ benutzt werden.
Die Pole (Nullstellen des Nenners)
und Nullstellen (Nullstellen des Zählers)
der Übertragungsfunktion sind die wichtigsten Kenngrößen des Systemverhaltens.
Sie sind entweder Null (fehlendes Endglied
der Differentialgleichung), reell
[
];
und [
]
oder konjugiert
komplex [
]
und [
].
Zur Bestimmung der Zeitkonstanten werden die Polynome der Übertragungsfunktion durch Nullstellenbestimmung in Linearfaktoren und Faktoren 2. Ordnung zerlegt. Wenn Zahlenwerte für die Koeffizienten der Polynome gegeben sind, können die Polynome durch die Nullstellenbestimmung faktorisiert werden.
Die Zerlegung der Zähler- und Nennerpolynome höherer Ordnung durch die Pole und Nullstellen ergibt mehrfache Linearfaktoren und mehrfache Faktoren 2. Ordnung. Als Voraussetzung dazu dürfen die Polynome in der Reihenfolge der Summenelemente entsprechend der Ordnungszahl keine Lücken aufweisen.
Werden diese Faktoren als unabhängige Einzel-Übertragungsfunktionen definiert, so entstehen je nach Art der Pole und der Nullstellen folgende Elementar-Übertragungsfunktionen:
- Die Abschlußterme der Differentialgleichung
sind Null: Der entstehende Linearfaktor ist eine Variable:
sowohl im Zähler als auch im Nenner.
- Die Pole bzw. die Nullstellen sind negativ reell. Aus [
] oder [
] entsteht der Linearfaktor in Zeitkonstantendarstellung [
] sowohl im Zähler als auch im Nenner.
- Die Pole bzw. die Nullstellen sind negativ konjugiert komplex. Aus [
] oder [
] entsteht der Faktor in Zeitkonstantendarstellung [
] 2. Ordnung sowohl im Zähler als auch im Nenner.
Beispiel einer Übertragungsfunktion mit der Polynomdarstellung, der Pol-Nullstellendarstellung und der Zeitkonstantendarstellung:
.
Zeitkonstanten der elementaren Einzelsysteme im Zähler und Nenner der Übertragungsfunktion
Die Zerlegung des Nennerpolynoms ergibt zeitverzögernd wirkende Einzelsysteme
(Linearfaktoren) und verzögernd wirkende Faktoren 2. Ordnung. Die Zerlegung des
Zählerpolynoms ergibt differenzierend wirkende Einzelsysteme (Linearfaktoren)
und differenzierend wirkende Faktoren 2. Ordnung. Letztere haben in Kombination
mit den zeitverzögernden Systemen des Nenners keinen Einfluss auf das
Zeitverhalten, sondern nur auf die Signalamplituden .
- Zeitkonstanten der Linearfaktoren als Variablen
mit Polen und Nullstellen gleich Null:
- Diese Linearfaktoren entstehen bei einer Laplace-Transformation einer
systembeschreibenden gewöhnlichen Differentialgleichung, deren Endglieder
oder
fehlen.
- Aus dem Produktterm
wird im Zähler und Nenner je
. Die in der nachstehenden Tabelle des nächsten Abschnitts dargestellten Zeitkonstanten
für das I-Glied
und
für das D-Glied
sind aus der Definition der Regler entnommen. In Wirklichkeit entsprechen sie Proportionalitätsfaktoren
oder
mit der Bewertung 1, wenn keine anderen Zahlenwerte angegeben worden sind.
- Zeitkonstante der Linearfaktoren mit Polen und Nullstellen gleich
:
- Die Definition der Zeitkonstante
eines
-Gliedes oder eines
-Gliedes errechnet sich wie folgt aus den Polen und Nullstellen für Zahlenwerte mit negativen Realteilen von
.
- Beispiel für die Definition einer Zeitkonstante aus dem Linearfaktor des
Zählers:
.
- Die Zeitkonstante errechnet sich allgemein aus dem Reziprokwert (Kehrwert)
einer negativen reellen Nullstelle
oder
des Nennerpolynoms oder Zählerpolynoms der Übertragungsfunktion als:
bzw.
.
- Zeitkonstanten des Faktors 2. Ordnung mit konjugiert komplexen Polen und Nullstellen:
- Aus der Pol-Nullstellendarstellung mit negativen konjugiert komplexen
Polen und Nullstellen entstehen Faktoren 2. Ordnung. Wird aus der
Nullstellendarstellung
für
die konjugiert komplexe Nullstelle [
] oder [
] eingesetzt, entsteht durch quadrieren zur Vermeidung der imaginären Größen, die Zeitkonstantendarstellung:
- Faktor 2. Ordnung in Pol-Nullstellendarstellung nach dem quadrieren:
- Mit
ergibt sich die Normalform der Zeitkonstantendarstellung des Faktors 2. Ordnung:
- Fazit:
- Dieser Faktor 2. Ordnung gilt sowohl für das Zähler- und Nennerpolynom und lässt sich nicht in kleinere mathematische Ausdrücke zerlegen.
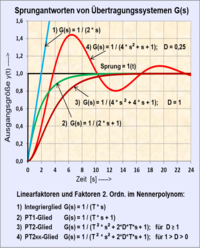
- Der Zeitverlauf einer normierten Sprungantwort eines Übertragungssystems
2. Ordnung mit konjugiert komplexen Polen (
-Glied) ist von der Zeitkonstante
und von der Dämpfung
abhängig.
Aufstellung und Verhalten der elementaren Einzelsysteme
Durch Zuordnung dieser Faktoren im Zähler und Nenner der
Übertragungsfunktionen können folgende 6 verschiedene stabile Elementarsysteme
einzeln oder mehrfach entstehen:
| Benennung | I-Glied | D-Glied | ||||
|---|---|---|---|---|---|---|
| Pol-Nullstellen | ||||||
| Übertragungsfunktion |
In der Zeitkonstanten-Darstellung entspricht die Zeitkonstante
dem Koeffizienten vor der komplexen Laplace-Variable
.
Die Berechnung des zeitlichen Verhaltens eines Gesamtübertragungssystems
erfordert immer, dass die Anzahl der Faktoren des Nenners immer gleich oder
größer sein muss, als die Anzahl der Faktoren im Zähler .
Differenzierende -Glieder
können das Zeitverhalten von verzögernden
-Gliedern
bei gleichen Zeitkonstanten vollständig kompensieren. Das Gleiche gilt natürlich
auch für
-Glieder
und
-Glieder.
Testsignale zur Prüfung des Systemverhaltens:
Übliche Testsignale für Übertragungssysteme sind: Sprungfunktion, Rücksprung, Impulsfunktion, Anstiegsfunktion und Sinusfunktion. Diese Signale werden ebenfalls vom Zeitbereich in den Bildbereich Laplace-transformiert. Siehe Definition der Testsignale im nächsten Abschnitt.
Zeitverhalten differenzierender Übertragungsglieder:
Das Zeitverhalten der Sprungantwort
oder der Impulsantwort
eines differenzierenden Systems des Zählerpolynoms kann allein grafisch nicht
dargestellt werden, weil die Änderung des Ausgangssignals im Zeitbereich
stattfindet. Das Zeitverhalten eines differenzierenden Systems lässt sich nur
mit einem Eingangssignal als Anstiegsfunktion grafisch darstellen.
Differenzierende Systeme ohne sogenannte zeitverzögernde parasitäre
-Glieder
lassen sich als Hardware technisch nicht herstellen. Die dazu notwendige
hinzugefügte parasitäre Zeitkonstante des zeitverzögernden
-Gliedes
muss wesentlich kleiner sein, als die Zeitkonstante des
-Gliedes
oder
-Gliedes.
Zeitverhalten von Übertragungsgliedern mit konjugiert komplexen Polen
(-Glieder):
Diese Übertragungsglieder 2. Ordnung enthalten Doppelpole im s-Bereich.
In Abhängigkeit von der Größe der Dämpfung
entsteht bei Anregung des Systems durch ein beliebiges Eingangssignal eine
gedämpft schwingende Ausgangsgröße. Häufig wird die Sprungantwort als
charakteristisches Verhalten dargestellt, bei dem die Ausgangsgröße exponentiell
asymptotisch mit einer Schwingungsüberlagerung einen Endwert erreicht.
Bei
lassen sich diese Systeme in zwei
-Glieder
zerlegen.
Die dem System zugehörigen Zeitkonstanten
liegen in quadratischer Form vor.
Übertragungssysteme mit Linearfaktoren oder Faktoren 2. Ordnung mit positivem Realteil der Pole:
Positive Realteile der Pole und Nullstellen ergeben negative Zeitkonstanten.
Übertragungsglieder mit positive Polen bilden instabile nichtlineare
Übertragungsfunktionen, die man mit z.B. mit „Instabilen T1-Gliedern“ oder
mit „Instabilen T2-Gliedern“ bezeichnen kann. Auch ihnen kann man Zeitkonstanten
zuordnen. Das Ausgangssignal dieser Systeme steigt nach einem positiven
beliebigen Eingangssignal
exponentiell progressiv bis zu einer Begrenzung an und kehrt erst zurück, wenn
das Eingangssignal negativ wird (Rückkopplungseffekt).
(Nähere Details siehe Regelstrecke#Charakterisierung
der Regelstrecken)
Berechnung des Zeitverhaltens von Übertragungsfunktionen
- Inverse Laplace-Transformation: Das System-Ausgangsverhalten
beliebiger Übertragungssysteme im Zeitbereich ist abhängig von der Übertragungsfunktion
und von der Art des Eingangssignals
. Mittels der inversen Laplace-Transformation lässt sich das Zeitverhalten mit Anwendung von Laplace-Transformationstafeln und dem Suchbegriff finden:
- Handelt es sich um eine normierte Sprungfunktion des Eingangssignals
, so ist
.
- Numerische Berechnung: Mit Hilfe der numerischen Mathematik durch
Berechnung von Differenzengleichungen
lassen sich für gegebene Eingangssignale
die Ausgangssignale
als nummerierte Folgegleichungen eines dynamischen Systems berechnen. Die Zeitkonstanten
in den Differenzengleichungen bestimmen das Verhalten der Einzelsysteme.
- Differenzengleichungen berechnen in Annäherung an eine kontinuierliche
Funktion
schrittweise eine Wertefolge
mit den Folgegliedern
für ein kleines Intervall
die Wertefolge
an der Stelle
, wobei
eine Nummerierung der errechneten Werte
darstellt.
Testsignale
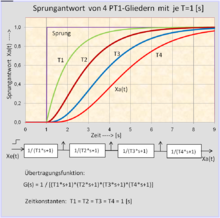
Den nichtperiodischen (deterministischen) Testsignalen kommt in der Systemtheorie eine zentrale Bedeutung zu. Mit ihrer Hilfe ist es möglich, ein Übertragungssystem zu testen, auf Stabilität zu prüfen oder Eigenschaften zu ermitteln.
Zur Berechnung des Zeitverhaltens eines Übertragungssystems können die
transformierten Testsignale im Bildbereich anstelle
mit der Übertragungsfunktion
des Systems multipliziert werden. Für die Rücktransformation von
in den Zeitbereich kann die gewünschte Gleichung der Systemantwort
mit Hilfe der Laplace-Transformationstafeln gefunden werden.
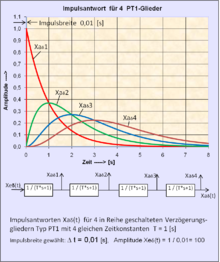
Den Testsignalen ist gemeinsam, dass sie zum Zeitpunkt
beginnen und bei
eine Amplitude = 0 aufweisen. Zur Unterscheidung der Funktion der Signale werden
sie mit den Zeichen δ (Impuls),
Ϭ (Sprung),
a (Anstieg) und s (Sinus)
indiziert.
Die Testsignale werden als Eingangsgröße
und als Laplace-transformierte Größe
wie folgt dargestellt.
| Begriff Testsignal u(t) |
Bildbereich Eingangssignal |
Systemantwort y(t) |
|---|---|---|
| Impulsfunktion δ oder Stoßfunktion, Deltaimpuls |
Impulsantwort oder Gewichtsfunktion | |
| Sprungfunktion σ |
Sprungantwort oder Übergangsfunktion | |
| Anstiegsfunktion oder Rampe |
Anstiegsantwort oder Rampenantwort | |
| Sinusfunktion s (Periodisches Signal) |
Frequenzgang |
Grundlagen der Ermittlung der Zeitkonstanten aus der gewöhnlichen Differentialgleichung 1. Ordnung
Eine lineare gewöhnliche Differentialgleichung 1. Ordnung mit konstanten
Koeffizienten
und
lautet:
-
.
Die Zeitkonstante
ist aus dieser Form der Differentialgleichung bereits berechenbar.
Allgemein wird für die Nullstellenbestimmung die höchste Ableitung einer
Differentialgleichung freigestellt, in dem sämtliche Terme der Gleichung durch
den zugehörigen Koeffizienten, in diesem Fall ,
dividiert werden. Damit lautet die neue mathematisch identische
Differentialgleichung:
.
Die Übertragungsfunktion G(s) dieser Differentialgleichung lautet für Anfangsbedingungen gleich Null nach Anwendung des Laplace-Differentiationssatzes:
.
Aus dem Verhältnis der Ausgangsgröße
zur Eingangsgröße
ergibt sich die Übertragungsfunktion in der Zeitkonstanten-Darstellung:
.
Bei dieser Form der Übertragungsfunktion
ist die Zeitkonstante
direkt ablesbar als Koeffizient vor der Laplace-Variable
mit dem Verhältnis der Koeffizienten
.
Setzt man für
und
in die Gleichung der Übertragungsfunktion ein, erhält man die Normalform der
Übertragungsfunktion eines Verzögerungsgliedes (
-Glied)
in der Zeitkonstanten-Darstellung:
Entstehung einer gewöhnlichen Differentialgleichung 1. Ordnung aus einem Hardware-Tiefpass
Ein durch eine gewöhnliche Differentialgleichung 1. Ordnung beschriebenes Verzögerungsglied (PT1-Glied) kommt in der Natur und in der Technik am häufigsten vor. Es entsteht z.B., wenn Wärme in ein Medium fließt oder eine elektrische Spannung an ein RC-Glied angelegt wird. Es interessiert immer, wie sich die Ausgangsgröße des Systems sich als Funktion der Zeit für eine gegebene Eingangsgröße verhält. Besonders anschaulich ist das Systemverhalten für eine gegebene Eingangsgröße als Sprungfunktion.
Das in der Elektrotechnik bekannteste dynamische System, welches durch eine
gewöhnliche Differentialgleichung 1. Ordnung beschrieben wird, ist das RC-Glied als
Widerstands-Kondensator-Schaltung mit der Zeitkonstante .
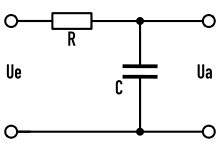
Ue: Eingangsspannung
Ua: Ausgangsspannung
Die allgemeine mathematische Beschreibung des RC-Gliedes ergibt sich über die Anwendung der Kirchhoffschen Gesetze.
Für das Hardware-Modell als Tiefpass gilt die Maschengleichung der Spannungen:
.
Dabei ist
die Eingangsgröße,
die gesuchte Ausgangsgröße. Wird für den Spannungsabfall
an R die Gleichung für den Ladestrom
in die obige Gleichung eingesetzt, entsteht die Differentialgleichung des
RC-Gliedes als Tiefpass:
Werden die üblichen Signalbezeichnungen der Systemtheorie angewendet, lauten
die neuen Signalbezeichnungen der gewöhnliche Differentialgleichung:
und
.
Für eine Differentialgleichung 1. Ordnung und der zugehörigen
Übertragungsfunktion
existiert kein Zähler- und Nennerpolynom. Es handelt sich bereits um einen
Linearfaktor im Nenner der Übertragungsfunktion. Deshalb hat die Nullstelle
keine Bedeutung.
Bei der üblichen Darstellung der Differentialgleichung wird die höchste
Ableitung von Koeffizienten freigestellt, indem sämtliche Terme der Gleichung
durch den zugehörigen Koeffizienten (hier )
dividiert werden. Damit lautet die neue mathematisch identische
Differentialgleichung:
Die Übertragungsfunktion G(s) dieser Differentialgleichung lautet für Anfangsbedingungen gleich Null nach dem Differentiationssatz:
.
Zusammengefasst als das Verhältnis der Ausgangsgrößen zur Eingangsgröße ergibt sich die Übertragungsfunktion in Zeitkonstanten-Darstellung:
-
.
Dabei entspricht der Koeffizient vor der Laplace-Variable
der Zeitkonstante
.
Entstehung
der Übertragungsfunktion  für einen Tiefpass (
für einen Tiefpass ( -Glied)
durch das Verhältnis komplexer Widerstände
-Glied)
durch das Verhältnis komplexer Widerstände
Im Gegensatz zur Übertragungsfunktion
kann der Frequenzgang
mit
eines linearen Übertragungssystems gemessen werden. Der Frequenzgang ist ein
Spezialfall der Übertragungsfunktion. Die Übertragungsfunktion kann jederzeit in
den Frequenzgang bei identischen Koeffizienten (Zeitkonstanten) überführt
werden. Die Entstehungsgeschichten des Frequenzgangs und der
Übertragungsfunktion sind unterschiedlich, die Schreibweisen können identisch
bleiben.
In der dargestellten RC-Schaltung kann das Verhältnis der Ausgangsspannung
zur Eingangsspannung auch als das Verhältnis der Ausgangsimpedanz zur
Eingangsimpedanz definiert werden. Setzt man für die Kapazität mit
den komplexen Widerstand
ergibt sich für das komplexe Widerstandsverhältnis als Übertragungsfunktion
:
Das Ergebnis entspricht dem aus der Differentialgleichung abgeleiteten -Glied.
Entstehung
der Übertragungsfunktion  für einen Hochpass durch das Verhältnis der komplexen Widerstände
für einen Hochpass durch das Verhältnis der komplexen Widerstände
Ersetzt man bei der RC-Schaltung die Kapazität C durch eine Induktivität L, entsteht bei der Betrachtung der Ein- und Ausgangsspannungen des Systems ein Hochpass 1. Ordnung. Bei Eingangssignalen mit hoher Frequenz hat die Induktivität einen hohen komplexen Widerstand. Mit fallender Frequenz fällt der induktive Widerstand ab.
In der dargestellten LC-Schaltung kann das Verhältnis der Ausgangsspannung
zur Eingangsspannung
auch als das Verhältnis der Ausgangsimpedanz zur Eingangsimpedanz definiert
werden. Setzt man für die Induktivität mit
den komplexen Widerstand
ergibt sich für das komplexe Widerstandsverhältnis als Übertragungsfunktion
:
Die Übertragungsfunktion des RL-Gliedes lautet mit :
Das Ergebnis entspricht einer Reihenschaltung eines -Gliedes
mit einem D-Glied. Für einen normierten Eingangssprung
springt das Ausgangssignal zur Zeit
auf
und fällt dann für
exponentiell asymptotisch auf den Wert
.
Das zu dieser Übertragungsfunktion zugehörige Zeitverhalten
lautet für einen Eingangssprung:
Die normierte Gleichung gilt für den Eingangssprung ;
.
Berechnung
des Zeitverhaltens eines  -Gliedes
nach einem Eingangssprung
-Gliedes
nach einem Eingangssprung
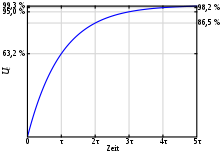
Häufig wird im Zeitbereich die Ausgangsgröße
der Übertragungsfunktion des
-Gliedes
(=
-Glied)
als Sprungantwort dargestellt. Der normierte Sprung für
lautet Laplace-transformiert:
.
Damit lautet die Übertragungsfunktion für
und
der Sprungantwort:
.
Ein evtl. vorhandener Verstärkungsfaktor
lässt sich nicht transformieren. Er erscheint auch nicht in den
korrespondierenden Laplace-Transformations-Tabellen der Rücktransformation und
kann im Zeitbereich unverändert übernommen werden.
Die Lösung im Zeitbereich der Sprungantwort
ergibt sich über die Korrespondenztabellen von Laplace-Transformationstafeln für
den Ausdruck:
:
ergibt das Zeitverhalten des Verzögerungsgliedes mit dem hinzugefügten
Verstärkungsfaktor .
-
)
Die normierte Gleichung gilt für den Eingangssprung
nach
.
.
Zeitverhalten des Rücksprungs
vom Anfangswert
des
-Gliedes
nach
.
-
Die normierte Gleichung gilt für den Rücksprung vonnach
.
Ausgangswerte eines -Gliedes
des Ansprungs
und des Rücksprungs
für ein- bis 5-fache Zeitkonstanten:
| Zeitkonstante T | Sprungantwort Ansprung: |
Sprungantwort Rücksprung: |
|---|---|---|
| T einfach | 63,2 | 36,8 |
| 86,5 | 13,5 | |
| 95,0 | 5,0 | |
| 98,2 | 1,8 | |
| 99,3 | 0,7 |
Diese normierte Gleichung gilt für den Eingangssprung .
ist der Verstärkungsfaktor,
.
Berechnungsbeispiel zur Bestimmung der Zeitkonstanten einer gewöhnlichen Differentialgleichung 2. Ordnung
-
Gegeben: Differentialgleichung eines Zeitgliedes 2. Ordnung ohne Differentiale der Eingangsgröße .
Anwendung der Laplace-Transformation der Differentialgleichung nach dem Differenziationssatz:.
und Freistellung der höchsten transformierten Ableitung:
.
:
und für
.
Damit lautet die Übertragungsfunktion und Freistellung des höchsten Exponenten (Gleichung dividiert durch):
.
Für die Lösung der Nullstellen (Pole) eines Polynoms 2. Ordnung kann die sogenannte pq-Formel benutzt werden:- Polynom:
.
.
Ergebnis:
Das Übertragungssystem mit zwei-Gliedern enthält die Zeitkonstanten
.
Eine Hardware-Nachbildung dieses Systems mit zwei RC-Gliedern in Reihenschaltung erfordert eine belastungsfreie Entkopplung.
Anmerkung:
Die Berechnung des Zeitverhaltens einer Übertragungsfunktion höherer Ordnung eines komplexen dynamischen Systems für eine gegebene Eingangsgröße besteht darin:
- Laplace-Transformationstafeln für die korrespondierende Zeitfunktion mit der normierten Übertragungsfunktion anzuwenden,
- oder eine faktorielle Form der Übertragungsfunktion in eine Partialbruch-Darstellung zu überführen, deren additive Terme einfach in den Zeitbereich überführt werden können,
- oder über die numerische Berechnung mit Differenzengleichungen,
welche aus den Linearfaktoren der Übertragungsfunktion abgeleitet sind, um das
Zeitverhalten von
für eine bestimmte Eingangsgröße
zu errechnen.
- Bei Übertragungsfunktionen höherer Ordnung mit einem Gemisch von negativen reellen Nullstellen und negativen konjugiert komplexen Nullstellen kann die Berechnung des Zeitverhaltens aus den Gleichungen der Laplace-Transformationstafeln mit den aufwendigen trigonometrischen Funktionen und Exponentialfunktionen recht kompliziert sein. Die numerische Berechnung mit Differenzengleichungen oder mit dem Erwerb von kommerziellen Simulations-Programmen ist erheblich einfacher.
Genormte Zeitkonstanten und Übergangsfrequenzen von Filtern
| Zeitkonstante τ in µs |
Übergangsfrequenz fc in Hz |
Entzerrungsnorm |
|---|---|---|
| 7958 | 20 | RIAA |
| 3183 | 50 | RIAA, NAB |
| 1592 | 100 | — |
| 318 | 500 | RIAA |
| 200 | 796 | — |
| 140 | 1137 | — |
| 120 | 1326 | MC |
| 100 | 1592 | — |
| 90 | 1768 | MC |
| 75 | 2122 | RIAA, FM USA |
| 50 | 3183 | NAB, PCM, FM Europa |
| 35 | 4547 | DIN |
| 25 | 6366 | — |
| 17,5 | 9095 | AES |
| 15 | 10610 | PCM |
Literatur
- Jan Lunze: Regelungstechnik 1. 6. Auflage. Springer Verlag, Berlin 2007, ISBN 978-3-540-70790-5. Regelungstechnik 2. 4. Auflage. Springer Verlag, Berlin 2006, ISBN 978-3-540-32335-8.
- Michael Laible: Mechanische Größen, elektrisch gemessen. Grundlagen und Beispiele zur technischen Ausführung. 7. Auflage. Expert Verlag, Renningen 1980, ISBN 3-8167-2892-8.
- Wolfgang Schneider: Praktische Regelungstechnik. Ein Lehr- und Übungsbuch für Nicht-Elektrotechniker. 3. Auflage. Vieweg+Teubner Verlag, Wiesbaden 2008, ISBN 978-3-528-24662-4.
- Walter Kaspers, Hans-Jürgen Küfner: Messen Steuern Regeln. 3. Auflage. Friedrich Vieweg & Sohn Verlag, Wiesbaden 1984, ISBN 3-528-24062-8.
Siehe auch
- Sigmoidfunktion
- Hochpass
- Tiefpass
- Bandpass
- Bandsperre
- Relaxationszeit
- Relaxation (Naturwissenschaft)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.05. 2024