Hochpass
Als Hochpass (auch Tiefensperre, englisch low-cut filter, high-pass filter) bezeichnet man Filter, die Frequenzen oberhalb ihrer Grenzfrequenz annähernd ungeschwächt passieren lassen und tiefere Frequenzen dämpfen.
Gebräuchlich sind solche Filter in der Elektronik, entsprechende Filterfunktionen können aber auch in anderen Bereichen, wie zum Beispiel Mechanik, Akustik, Hydraulik oder Elektrotechnik vorkommen, sie werden dort meistens jedoch nicht so genannt.
Anwendungen
Hochpass-Filter in der Niederfrequenztechnik werden anwendungsbezogen auch als Tiefen-Sperre, Bassfilter, Low-Cut-Filter, Bass-Cut-Filter, Trittschallfilter bezeichnet. Diese Begriffe sind in der Tontechnik gebräuchlich; sie weisen darauf hin, dass ein solcher Filter, zum Beispiel in einem Equalizer die „Tiefen“ des Signals bzw. entsprechende Brummstörungen abschwächt, die vorwiegend tiefe Frequenzen enthalten. Weiterhin sind Hochpässe den Hochtonlautsprechern (Tweeter) vorgeschaltet.
Hochpässe werden auch zur Ein- und Auskopplung von Hochfrequenzsignalen, z.B. in Antennenweichen, bei ADSL oder der HF-Signalübertragung über Energieleitungen eingesetzt.
Mit Hilfe von Filter-Transformationen kann aus dem Hochpass ein Tiefpass oder auch eine Bandsperre gebildet werden.
Hochpass 1. Ordnung
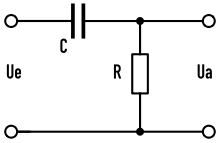
Als Beispiel für einen Hochpass ist im Folgenden die Funktion einer
elektrischen Filterschaltung
gegeben. Das Bild zeigt den grundsätzlichen Aufbau aus einem Kondensator
C und einem Widerstand
R. Bei niedriger Frequenz sperrt der Blindwiderstand
()
des Kondensators weitgehend den Strom.
Von der Eingangsspannung
erscheint am Ausgang gemäß der Spannungsteilerformel
nur der Anteil
:
(Herleitung siehe Tiefpass-Formel-Herleitung)
Phasengang:
wobei
und
die Beträge der Ein- und Ausgangsspannung bezeichnen.
Die Grenzfrequenz
(engl.: cutoff frequency) eines solchen Hochpasses ist
. Unter der Grenzfrequenz
versteht man diejenige Frequenz,
bei der
ist, d.h.,
ist gegenüber
um 3 Dezibel
abgeschwächt. Die Dämpfung nimmt unterhalb der Grenzfrequenz um 20 Dezibel pro
Dekade
zu. Bei einer logarithmischen Darstellung auf beiden Achsen ergibt das eine
Gerade. Da
mit steigender Frequenz kleiner wird, geht das Teilungsverhältnis mit steigender
Frequenz gegen 1, für hohe Frequenzen wird
.
mit
Die Dämpfung beträgt dann 0 dB.
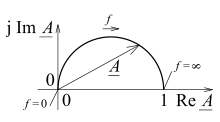
Der Frequenzgang der Schaltung wird auch gerne durch eine Ortskurve in der komplexen Ebene dargestellt. Dabei stellt A das Spannungsverhältnis in komplexer Schreibweise dar:
.
Die Länge des von der Zeit unabhängigen Zeigers A steht für das Amplitudenverhältnis, wie es sich mit der Frequenz ändert; der Winkel zur positiven reellen Achse steht für φ.
Hochpass 2. Ordnung

Einen Hochpass zweiter Ordnung erhält man, indem man R durch eine Induktivität L ersetzt, da diese ihrerseits eine – und zwar zum Kondensator gegenläufige – Frequenzabhängigkeit besitzt, und einen Widerstand R in Reihe mit dem Kondensator C schaltet. Dabei wird R so groß gewählt, dass keine oder nur eine geringe Resonanzüberhöhung des Frequenzgangs entsteht.
Der Frequenzgang eines solchen Hochpasses ist
- mit
.
Der Betrag der Übertragungsfunktion ist
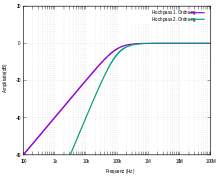
Damit reduziert sich die Ausgangsspannung unterhalb von fG stärker (mit 40 dB/Dekade) ab, da nun nicht nur |XC| größer, sondern zugleich XL kleiner wird.
Bei der statischen Frequenzgangveränderung, der Emphasis und der Deemphasis wird anstatt der Grenzfrequenz üblicherweise die Zeitkonstante angegeben.
Hochpässe zweiter und höherer Ordnung werden heute üblicherweise durch Operationsverstärker-Schaltungen realisiert. Diese Filter werden als aktive Hochpässe (bzw. aktive Filter) bezeichnet und sind auch nach ihren Erfindern als Sallen-Key-Filter bekannt.
Hochpass n-ter Ordnung
Durch Hintereinanderschaltung mehrerer Hochpässe wird deren Ordnung erhöht. Zwei hintereinander geschaltete Hochpässe 2. Ordnung bilden demnach einen Hochpass 4. Ordnung. Die Dämpfung ändert sich hierbei unterhalb der Grenzfrequenz mit:
,
was einer Flankensteilheit
von 24 dB/Oktave entspricht. 6 dB pro Oktave sind gleich 20 dB
pro Dekade: eine Änderung um eine Oktave (Änderung um Faktor 2) entspricht der
-fachen
Änderung um eine Dekade:
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.05. 2024