Bel (Einheit)

Physikalische Einheit
Einheitenname	Bel
Einheitenzeichen	$\mathrm {B}$
Physikalische Größe(n)	Pegel und Maße
Formelzeichen	$Q,\,L$ (Pegel), $A,\,G$ (Maße)
Dimension	${\mathsf {1}}$
Benannt nach	Alexander Graham Bell
Siehe auch: Neper

Das Bel (Einheitenzeichen B) ist eine nach Alexander Graham Bell benannte Hilfsmaßeinheit zur Kennzeichnung des dekadischen Logarithmus des Verhältnisses zweier Größen der gleichen Art bei Pegeln und Maßen. Diese werden u.a. in der Elektrotechnik und in der Akustik angewendet, beispielsweise bei Angaben zu Dämpfungen und Verstärkungen, Spannungen und Schalldruck.

In der Regel wird statt des Bels das Dezibel (Einheitenzeichen dB) verwendet, also der zehnte Teil eines Bels.

Anders als in anderen europäischen Staaten ist das Dezibel in der Schweiz und in Österreich eine gesetzliche Einheit.

Definition von Bel und Dezibel

Gebräuchlicher als Bel ist das Dezibel, das mit Hilfe des Einheitenvorsatzes „Dezi“ (Vorsatzzeichen d) gebildet wird:

${\begin{aligned}1\,\mathrm {dB} &={\frac {1}{10}}\,\mathrm {B} \\10\,\mathrm {dB} &=1\,\mathrm {B} \end{aligned}}$

Das Bel (oder Dezibel) dient zur Kennzeichnung des Pegels $Q_{{(P)}}$ , also des dekadischen Logarithmus des Verhältnisses zweier gleichartiger Energie- bzw. Leistungsgrößen $P_{1}$ und $P_{2}$ :

Umrechnung: Beispiele
	$P_{1}/P_{2}$	$F_{1}/F_{2}$
40 dB	10000	100
20 dB	100	10
10 dB	10	≈ 3,16
6 dB	≈ 4	≈ 2
3 dB	≈ 2	≈ 1,41
1 dB	≈ 1,26	≈ 1,12
0 dB	1	1
−1 dB	≈ 0,79	≈ 0,89
−3 dB	≈ 0,5	≈ 0,71
−6 dB	≈ 0,25	≈ 0,5
−10 dB	0,1	≈ 0,32
−20 dB	0,01	0,1
−40 dB	0,0001	0,01

$Q_{(P)}=\lg {\frac {P_{1}}{P_{2}}}\,\mathrm {B} =10\,\lg {\frac {P_{1}}{P_{2}}}\,\mathrm {dB}$

In linearen Systemen verhalten sich die Leistungsgrößen proportional zu den Quadraten der Effektivwerte von einwirkenden Feldgrößen (z.B. elektrische Spannung, Schalldruck). Entsprechend ist die Benennung „Feldgröße“ in der Normung durch die Benennung „Leistungswurzelgröße“ ersetzt worden.

$P\sim F^{2};\quad {\frac {P_{1}}{P_{2}}}={\frac {F_{1}^{2}}{F_{2}^{2}}}=\left({\frac {F_{1}}{F_{2}}}\right)^{2};\quad \lg {\frac {P_{1}}{P_{2}}}=2\cdot \lg {\frac {F_{1}}{F_{2}}}.$

Soll von Leistungswurzelgrößen ausgehend das Leistungsverhältnis berechnet werden, so gilt damit:

$Q_{{(F)}}=10\,\lg {\frac {F_{1}^{2}}{F_{2}^{2}}}\,{\mathrm {dB}}=20\,\lg {\frac {F_{1}}{F_{2}}}\,{\mathrm {dB}}.$

Die logarithmischen Verhältnisse der Leistungsgrößen und der Leistungswurzelgrößen unterscheiden sich um den Faktor zwei, siehe auch die Umrechnungstabelle.

Umrechnung in die Einheit Neper

Dezibel und Neper dienen beide der Kennzeichnung der Logarithmen von Verhältnissen. Sie unterscheiden sich um einen festen Faktor. Mit der Festlegung

$Q_{{(F)}}=20\lg {\frac {F_{1}}{F_{2}}}\,{\mathrm {dB}}=\ln {\frac {F_{1}}{F_{2}}}\,{\mathrm {Np}},$

wobei $\ln$ den natürlichen Logarithmus bezeichnet, und mit der für jedes > 0 gültigen Umrechnung

$\ln x=\lg x\cdot \ln 10$

ist unabhängig von $F_{1}/F_{2}$

$20\;{\mathrm {dB}}=\ln 10\;{\mathrm {Np}};\quad 1\;{\mathrm {dB}}\approx 0{,}1151\;{\mathrm {Np}};\quad 1\;{\mathrm {Np}}\approx 8{,}686\;{\mathrm {dB}}.$

Dezibel und Neper, historische Entwicklung

Obwohl nicht das Bel bzw. Dezibel, sondern das Neper die zum Internationalen Einheitensystem SI kohärente Hilfsmaßeinheit für logarithmische Verhältnisgrößen ist, wird in der Praxis überwiegend das Dezibel verwendet. Das hat zum einen historische Gründe: In den USA war bis 1923 als Einheit für das Dämpfungsmaß einer Fernsprechverbindung die Hilfsmaßeinheit „Mile Standard Cable“ (m.s.c.) in Verwendung. Diese Einheit entspricht dem Dämpfungsmaß eines bestimmten Kabeltyps („19 gauge“) bei einer Länge von einer englischen Meile und einer Frequenz von 800 Hz und gleichzeitig der mittleren subjektiven Wahrnehmbarkeitsschwelle beim Vergleich von zwei Lautstärken. Letzteres trifft ebenfalls für das Dezibel zu. Deshalb ergaben sich bei Verwendung des Dezibels in etwa die gleichen Zahlenwerte wie bei Verwendung von „Mile Standard Cable“ (1 m.s.c. = 0,9221 dB). Ein weiterer Grund für die bevorzugte Verwendung des Dezibels ist, dass sich einfach fassbare Zahlenwerte ergeben. So ist z. B. die Verdopplung der Leistung als Leistungsgröße eine Änderung von etwa 3 dB und die Verzehnfachung eine Änderung von 10 dB. Dagegen ist jedoch z.B. die Verdopplung der Spannung bzw. des Schalldrucks als Feldgröße eine Änderung von etwa 6 dB und die Verzehnfachung eine Änderung von 20 dB.

Um einem häufigen Missverständnis vorzubeugen: Eine Pegeländerung ist nicht getrennt für z.B. Spannung und Leistung zu bestimmen. Es gelten dieselben Pegeländerungen. So bedeutet +6 dB eine Verdoppelung der Spannung, was einer Vervierfachung der Leistung entspricht.

Verwendung mit anderen Maßeinheiten, Zusätze

Wie jede andere Maßeinheit kann das Bel bzw. Dezibel zusammen mit anderen Maßeinheiten verwendet werden, wenn damit eine Größe beschrieben wird, bei der ein Pegel oder Maß durch Multiplikation oder Division mit einer anderen Größe verknüpft wird. Beispiele dafür sind das Dämpfungsmaß einer Leitung in Dezibel pro Meter (dB/m) oder der bezogene Schallleistungspegel einer ausgedehnten Schallquelle in Dezibel pro Quadratmeter (dB/m²).

Nach den für Größen geltenden Rechenregeln ist es zwar nicht korrekt, Zusätze an eine Einheit anzubringen, um Informationen über die Art der betrachteten Größe mitzuteilen, doch sind solche Zusätze beim Dezibel z.B. in den Empfehlungen der ITU noch gebräuchlich. Wegen der Eindeutigkeit und der möglichen Verwechslungsgefahr mit Einheitenprodukten (z.B. dB·m statt dBm) sind nach den Festlegungen in DIN, IEC und ISO-Normen diese Informationen stets mit der Größe und nicht mit der Einheit zu verknüpfen. Die geläufigsten Beispiele für dB-Zusätze sind in der folgenden Tabelle zusammengefasst:

Einheit mit Suffix (ITU)	Bedeutung	Schreibweise gemäß DIN, IEC, ISO
dBu	Spannungspegel mit der Bezugsgröße ${\sqrt {600\,\Omega \cdot 1\,{\mathrm {mW}}}}\,\approx 0{,}7746\,{\mathrm V}$	$L_{u}({\mathrm {re\;0{,}775\,V}})=\dots \,{\mathrm {dB}}$
dBV	Spannungspegel mit der Bezugsgröße 1 V	$L_{V}({\mathrm {re\;1\,V}})=\dots \,{\mathrm {dB}}$
dBA	A-bewerteter Schalldruckpegel mit der Bezugsgröße $\mathrm {\;20\,\mu Pa}$	$L_{{pA}}({\mathrm {re\;20\,\mu Pa}})=\dots \,{\mathrm {dB}}$
dBA	A-bewerteter Schallleistungspegel	$L_{{WA}}({\mathrm {re\;1\,pW}})=\dots \,{\mathrm {dB}}$
dBm	Leistungspegel mit der Bezugsgröße 1 mW	$L_{P}({\mathrm {re\;1\,mW}})=\dots \,{\mathrm {dB}}$
dBW	Leistungspegel mit der Bezugsgröße 1 W	$L_{P}({\mathrm {re\;1\,W}})=\dots \,{\mathrm {dB}}$
dBµ	Pegel der elektrischen Feldstärke mit der Bezugsgröße 1 µV/m	$L_{E}({\mathrm {re\;1\,\mu V/m}})=\dots \,{\mathrm {dB}}$

Darüber hinaus existiert noch eine große Anzahl weiterer Zusätze, die in verschiedenen Fachgebieten uneinheitlich verwendet werden. Für viele Pegelgrößen existieren genormte Bezugswerte.

Anwendung

Beispiel für Darstellung mit linearer Größe: Übertragungsfaktor $u_{o}/u_{i}$ eines Butterworth-Filters 2. Ordnung

Beispiel für Darstellung mit logarithmischer Größe: Übertragungsmaß $A_{0}$ eines Butterworth-Filters 2. Ordnung

In beiden Darstellungen ist die vertikale Achse linear geteilt, die horizontale logarithmisch.

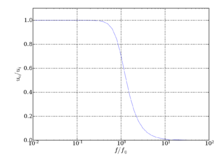
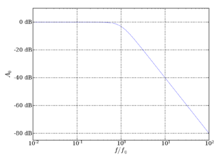
Die Angabe von Pegeln, Pegeldifferenzen und Maßen spielt in verschiedenen Fachgebieten eine Rolle. Vor allem in der Akustik und der Tontechnik, der Nachrichtentechnik und der Hochfrequenztechnik sowie in der Automatisierungstechnik haben die verwendeten Größen oft Wertebereiche über etliche Zehnerpotenzen. Die Angabe als logarithmische Verhältnisgröße erlaubt oft eine schnelle und anschauliche Interpretation von Größen, wenn gewisse Zusammenhänge im Bereich kleiner Werte genauso deutlich gemacht werden sollen wie im Bereich großer Werte. Ferner kann das Rechnen vereinfacht sein, wenn z.B. über mehrere Verstärkerstufen die Spannungsverstärkungen zu multiplizieren sind und die Verstärkungsmaße zu addieren.

In allen diesen technischen Anwendungen wird der dekadische Logarithmus zusammen mit dem Dezibel bevorzugt, zumal diese Darstellung eine einfache Zehnerpotenzabschätzung ermöglicht. Nur in theoretischen Abhandlungen wird der natürliche Logarithmus bevorzugt.

Der menschliche Sinneseindruck verläuft in etwa logarithmisch zur Intensität des physikalischen Reizes (Weber-Fechner-Gesetz). Damit entspricht der Pegel der einwirkenden physikalischen Größe linear dem menschlichen Empfinden. Das hat beispielsweise für die Akustik Bedeutung, wo auch die Maßeinheit der psychoakustischen Größe Lautstärke, das Phon, durch eine Verknüpfung mit dem physikalischen Schalldruckpegel in Dezibel definiert ist.

Siehe auch

Typische Schalldruckpegel verschiedener Geräusche

Basierend auf einem Artikel in:

Wikipedia.de