Zustandsraumdarstellung

Die Zustandsraumdarstellung ist eine von mehreren bekannten Formen der Systembeschreibung eines dynamischen Übertragungssystems. Das Zustandsraummodell gilt als ingenieurtechnisch geeignete Methode der Analyse und Synthese dynamischer Systeme im Zeitbereich und ist besonders effizient bei der regelungstechnischen Behandlung von Mehrgrößensystemen, nichtlinearen und zeitvariablen Übertragungssystemen. Dabei werden sämtliche Beziehungen der Zustandsgrößen, der Eingangsgrößen und Ausgangsgrößen in Form von Matrizen und Vektoren dargestellt. Das Zustandsraummodell wird durch zwei Gleichungen – die Zustandsdifferenzialgleichung erster Ordnung und die Ausgangsgleichung – beschrieben.

Grundlagen der Systembeschreibung im Zustandsraum

Die seit den 1960er Jahren bekannte Theorie des Zustandsraumes stammt aus den USA von dem Mathematiker und Stanford-Universitätslehrer Rudolf E. Kálmán. Sie ist etwa zeitgleich mit dem Auftreten erster leistungsfähiger Digitalrechner entstanden, die für den Umgang mit der Zustandsraumdarstellung unverzichtbar sind.

Im Hochschulbereich der ingenieurwissenschaftlichen Fachrichtungen der Automatisierung, Mechatronik, Elektrotechnik usw. nimmt insbesondere in der Regelungstechnik die Zustandsraumdarstellung zunehmend einen größeren Bereich ein. So gilt nach Darstellung einiger Hochschullehrer die Zustandsraumdarstellung bereits in der Vergangenheit als wesentlicher technologischer Impuls für die Luft- und Raumfahrt wie der im Apollo-Programm 1969 vollzogene Flug zum Mond.

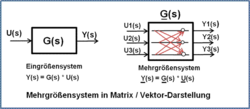
Unter dem Begriff Zustandsraumdarstellung versteht man die Beschreibung eines dynamischen Übertragungssystems durch seine Zustandsgrößen (= Zustandsvariablen). Dabei wird die systembeschreibende Differenzialgleichung n-ter Ordnung mit n konzentrierten Energiespeichern in n Differenzialgleichungen 1. Ordnung zerlegt und in eine Matrizen/Vektor-Darstellung gebracht.

Die Zustandsvariablen beschreiben physikalisch den Energiegehalt der in einem technischen dynamischen System enthaltenen Speicherelemente. Sie bedeuten z.B. Spannung an einem Kondensator, Strom in einer Induktivität, bei einem Feder-Massesystem die potentiellen und kinetischen Energieanteile. Die Anzahl der Zustandsvariablen $x_{1}(t)\cdots x_{n}(t)\,$ des Zustandsvektors ${\underline {x}}(t)\,$ ist die Dimension des Zustandsraumes. Im Zustandsvektor ${\underline {x}}(t)\,$ zum beliebigen Zeitpunkt t₍₀₎ sind alle Informationen des dynamischen Übertragungssystems enthalten.

Wesentliche Begriffe zum Verständnis der Beschreibung eines Übertragungssystems im Zustandsraum sind das Zustandsraummodell und die angewandte Normalform, nach der die Zustandsgleichungen und zugehörigen Matrizen / Vektoren ausgelegt sind. Das Zustandsraummodell kann für nicht sprungfähige Systeme direkt aus den Koeffizienten der systembeschreibenden Differenzialgleichung oder der zugehörigen Übertragungsfunktion erstellt werden.

Nach dem Signalflussplan der Regelungsnormalform kann mit Hilfe der zurückgeführten Zustandsvariablen ein dynamisch vorteilhafter Zustands-Regelkreis gebildet werden, der ohne Matrizendarstellung mittels numerischer Berechnung aller vorliegenden Signalgrößen simuliert werden kann.

Übersicht der Systembeschreibungen

In der klassischen Regelungstheorie vor den 1960er Jahren hatte die Analyse und Berechnung von Regeleinrichtungen im Zeitbereich nur eine geringere Bedeutung als die Methoden im Frequenz- und s-Bereich, wie die Laplace-Transformation, der Frequenzgang und das Wurzelortsverfahren. Dabei wurden hauptsächlich lineare zeitinvariante Übertragungsglieder mit konstanten Koeffizienten behandelt. Nichtlineare Systeme wurden linearisiert.

Zum Verständnis der Theorie der Zustandsraumdarstellung sind folgende Kenntnisse der Systembeschreibungen erforderlich:

Gewöhnliche Differenzialgleichungen eines Übertragungssystems

Die Beschreibung von linearen Systemen mit konzentrierten Energiespeichern (im Gegensatz zu Systemen mit verteilten Speichern → Partielle Differenzialgleichung) erfolgt mit gewöhnlichen Differenzialgleichungen. Die Differenzialgleichung beschreibt ein lineares Übertragungssystem mit n Energiespeichern durch n Ableitungen der Systemausgangsgröße y(t) und m Ableitungen der Eingangsgröße u(t) des Systems.

Beispiel der Beschreibung eines Verzögerungsgliedes 1. Ordnung (PT1-Glied):

$T_{1}\cdot {\frac d{dt}}y(t)+y{(t)}=K_{{PT1}}\cdot u(t)$

mit $T_{1}$ als die System-Zeitkonstante und dem Verstärkungsfaktor $K_{PT1}$ .

Beschreibung linearer Systeme im komplexen Frequenzbereich

Blockdiagramm eines Übertragungssystems als Ein- und Mehrgrößensystem.

Die Übertragungsfunktion ist eine mathematische Beschreibung für das Verhalten eines linearen, zeitinvarianten Systems im Frequenzbereich (s-Bereich) mit der komplexen Variablen s. Sie ist in der Regelungstechnik die häufigste Darstellungsform für die Beschreibung des Eingangs- und Ausgangsverhaltens von Übertragungssystemen.

Sämtliche Systemeigenschaften wie die Kriterien der Stabilität, Pole, Nullstellen, Verstärkung und Zeitkonstanten können aus der Übertragungsfunktion abgeleitet werden. Durch die Rücktransformation mittels der Laplace-Transformation kann das zeitliche Verhalten eines Übertragungssystems als Funktion des Eingangssignals berechnet werden.

Eine wesentliche Erkenntnis in der linearen Systembeschreibung ist die Tatsache, dass Differenzialgleichungen wie auch Übertragungsfunktionen in Polynomdarstellung beliebiger Ordnung auf 3 einfache Grundformen von Polynomen zerlegt werden können, die ein völlig unterschiedliches signaltechnisches Verhalten haben, ob sie im Zähler oder Nenner der Übertragungsfunktion stehen.

Siehe auch: Charakterisierung der Regelstrecken

Beispiel der Beschreibung eines Verzögerungsgliedes 1. Ordnung (PT1-Glied):

$G(s)={\frac {Y(s)}{U(s)}}={\frac {K_{{PT1}}}{T_{1}\cdot s+1}}$

Numerische Beschreibung linearer und nichtlinearer Systeme

Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen, Begrenzungseffekten und Totzeitsystemen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Abhilfe bietet die numerische Berechnung im diskreten Zeitbereich Δt.

Anstelle der Berechnung des kontinuierlichen Verhaltens der physikalischen Größen eines dynamischen Systems als f(t) erfolgt die Umsetzung in eine quantisierte Berechnungsmethode mit konstanten kleinen Zeitintervallen, der diskreten Zeit Δt. Das dynamische System wird in seiner einfachsten Form durch 4 unterschiedliche Differenzialgleichungen erster Ordnung mit Differenzengleichungen beschrieben und algebraisch rekursiv berechnet. Wesentliches Merkmal der Rekursion ist die Folge k = (0, 1, 2, 3, …, k_n), bei dem das Rechenergebnis der zurückliegenden Folge k-1 zu dem aktuellen diskreten Rechenergebnis der Folge k hinzu addiert wird.

Beispiel der Beschreibung eines Verzögerungsgliedes 1. Ordnung (PT1-Glied mit dem Verstärkungsfaktor K_PT1) nach der Euler-Approximation:

$Y_{(k)} = Y_{(k-1)} + (K_{PT1} \cdot U_{(k)} -Y_{(k-1)})\cdot \frac {\Delta t}{T_1 + \Delta t}; \qquad t = k \cdot \Delta t$

Für die numerische Berechnung von Übertragungssystemen stehen verschiedene Rechenprogramme zur Verfügung.

Definition des Zustandes eines Übertragungssystems

Während die vorstehenden Systembeschreibungen das Übertragungsverhalten eines Systems beschreiben, bedeutet die Beschreibung eines Systems im Zustandsraum, der momentane Zustand des Systems zu einer bestimmten Zeit t = 0.

Physikalisch betrachtet ist der Zustand eines dynamischen Systems durch den Energiegehalt der im System vorhandenen Energiespeicher bestimmt. Die Zustandsgrößen beschreiben den Energiegehalt der im System enthaltenen Speicherelemente. Sie können sich bei Anregung des Systems nicht sprunghaft ändern.

Den Wert der Zustandsgrößen $x_{1},x_{2}\cdots x_{n}\,$ zu diesem bestimmten Zeitpunkt t ist der Zustand des Systems und wird durch den Vektor ${\underline {x}}(t)\,$ zusammengefasst.

Das Verhalten des Übertragungssystems ist zu einem beliebigen Zeitpunkt zu der Zeit t = 0 für t > 0 vollständig gegeben, wenn

das mathematische Modell des Übertragungssystems bekannt ist,
die Anfangswerte $x(t=0)=x(0)\,$ der Energiespeicher bekannt sind und
die Eingangsgrößen des Systems bekannt sind.

Daraus folgt:

Bei Kenntnis des Systemzustandes und aller auf das System einwirkenden Signalgrößen kann das zukünftige Systemverhalten für t > 0 vorausbestimmt werden.

Zustand eines dynamischen Systems im Zustandsraum = Zustandsvektor $\underline {x}\,$ zum Zeitpunkt $t \,$ .

Der Zustandsvektor ${\underline {x}}(t)\,$ eines linearen Systems bestimmt mit dem Verlauf des Eingangssignals u(t) vollständig den Verlauf der Ausgangsgröße y(t) für $t >t_0 \,$ .
Die Anzahl der Zustandsvariablen von ${\underline {x}}(t)\,$ ist die Dimension des Zustandsraumes.

Begriffsdefinitionen: Zustandsraum, Vektorraum, Phasenraum, Phasenporträt

Im deutschen Sprachraum ist der Begriff der Zustandsraumdarstellung für den älteren und auch heute gültigen Begriff Systembeschreibung im Zustandsraum erst nach den 1970er Jahren entstanden.

Laut der Fachliteratur der Regelungstechnik ist der Einzelbegriff „Zustandsraum“ eines dynamischen Übertragungssystems wie folgt definiert:

Der „Zustandsraum“ ist der dem Zustandsvektor $\underline {x}(t)$ zugehörige n-dimensionale Vektorraum, in dem sich jeder Zustand als Punkt und jede Zustandsänderung des Übertragungssystems sich als Teil einer Bahnkurve (Trajektorie) darstellt.

Wegen der Ähnlichkeit der Definition des Begriffs „Zustandsraum“ mit dem mathematischen Begriffen Vektorraum und Phasenraum darf man davon ausgehen, dass der Begriff Zustandsraum aus dem Primärbegriff „Zustand eines Systems“ und dem Begriff „Phasenraum“ entstanden ist.

Das Systemverhalten eines dynamischen Übertragungssystems im Zustandsraum am Beispiel eines Verzögerungssystems höherer Ordnung lässt sich besonders grafisch anschaulich darstellen durch:

Grafische Darstellung des Phasenporträts

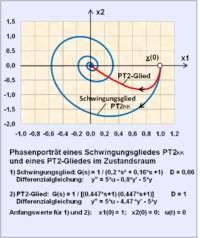
Phasenporträt eines PT2-Schwingungsgliedes und eines PT2-Gliedes im Zustandsraum.

Bei der Zustandsraumdarstellung für zweidimensionale Systeme spannt der $x_1 / x_2 \,$ -Raum eine Fläche auf. Diese Beziehung wird mit Phasenraum und die sich ergebende Trajektorie wird mit Phasenporträt bezeichnet.

Das Phasenporträt für Systeme ohne Eingangssignal u(t) = 0 wird stets im Uhrzeigersinn zum Ursprung durchlaufen, vorausgesetzt, das System ist stabil.

Für 2- oder 3-dimensionale Zustandsvektoren sind zum Verständnis grafische Konstruktionen möglich.

Sind z.B. für ein PT2-Schwingungsglied mit der Dämpfung D = 0,06 die Eingangsgröße u(t) = 0 und die Anfangswerte $x_{1}(0)=1\,$ und $x_{2}(0)=0\,$ gegeben, dann verläuft die Bahnkurve (Phasenporträt) als Funktion der Zeit in dem x1-x2-Diagramm entsprechend der Eigenbewegung des Systems von einem Anfangswert $x_{1}(0)=1\,$ spiralförmig (typisch für ein Schwingungsglied) zum Ursprung Null ( $x_{1}(t)=x_{2}(t)=0\,$ ) nach endlicher, genügend langer Zeit.

Die Bahnkurve eines PT2-Gliedes mit der Dämpfung D = 1 und gleichen Anfangswerten kann den Ursprung – wie im Bild dargestellt – nicht umschlingen, sondern erreicht ihn von einem abfallenden Anfangsgradienten auf dem kürzesten Weg.

Aufzeichnung des Verlaufs der Zustandsvariablen f(t)

Durch Aufzeichnung des Verlaufs der Zustandsvariablen als Funktion der Zeit nach einem System-Eingangssprung u(t) wird ersichtlich, dass die Zustandsvariablen $x_{2}(t)\cdots x_{n}(t)\,$ des Übertragungssystems sich dynamisch deutlich schneller verhalten, als die Ausgangsgröße $y(t)=x_{1}(t)\,$ .

Die Nutzung dieser vorteilhaften Eigenschaft ist von großer Bedeutung für das Regelverhalten eines Zustandsregelkreises. Die prägenden Begriffe für den Zustandsregelkreis sind Zustandsrückführung und zum konventionellen Gegenstück Ausgangsrückführung.

Siehe im Abschnitt Regelungsnormalform, drittes Bild „Grafische Darstellung der Zustandsvariablen“.

Beispiel Zustandsvariablen und Zustandsgleichungen für ein PT2-Schwingungsglied

Standard-Übertragungsfunktion eines Schwingungsgliedes (PT2-Glied) mit konjugiert komplexen Polen (PT2_KK-Glied):

$G(s)={\frac {Y{(s)}}{U{(s)}}}={\frac 1{T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}}$

Die zugehörige lineare Differenzialgleichung wird durch Umwandlung mit Hilfe der inversen Laplace-Transformation ermittelt:

$T^{2}\cdot {\ddot {y}}(t)+2\cdot D\cdot T\cdot {\dot {y}}(t)+y(t)=u(t)\,$

In der Fachliteratur werden zur Vereinheitlichung die Koeffizienten der Ableitungen von y(t) (hier T², 2 D T) mit dem Buchstaben a dargestellt, für die rechte Seite der Ableitungen von u(t) mit b und fortlaufend nummeriert:

$a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)\,$

Die höchste Ableitung wird vom Koeffizienten freigestellt, in dem alle Terme der Gleichung durch a_2 dividiert werden und nach ${\ddot {y}}(t)$ aufgelöst wird:

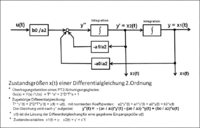
$\ddot{y}(t) = \frac 1 {a_2} \cdot (- a_0 \cdot y(t) -a_1 \cdot \dot{y}(t) + b_0 \cdot u(t))$

Blockschaltbild eines Signalflussplanes zur Bestimmung der Zustandsvariablen im Zustandsraum.

Das in dem Strukturbild dargestellte Blockschaltbild entspricht der klassischen Variante der Lösung einer Differenzialgleichung mit Hilfe der Analogrechentechnik. Dieses Verfahren ist seit langem bekannt. Das Interesse galt natürlich nur dem Verhalten der Ausgangsgröße y(t).

Jede Ableitung der Ausgangsgröße y(t) wird einer Integration unterzogen. Jede Zustandsgröße wird mit dem zugehörigen Koeffizienten auf den Eingang zurückgeführt und von der Eingangsgröße u(t) subtrahiert.

Eine Differenzialgleichung n-ter Ordnung benötigt zur Lösung n Integrationen. Nach dem Blockschaltbild zur Lösung der Differenzialgleichung 2. Ordnung ergeben sich 2 Zustandsvariablen als Ausgänge der Integratoren. Durch Substitution werden die Ableitungen von y(t) durch die Bezeichnung der Zustandsvariablen x(t) wie folgt eingesetzt:

$x_{1}(t)=y(t);\qquad x_{2}(t)={\dot {y}}(t)$

Damit lautet die Differentialgleichung mit den eingeführten neuen Bezeichnungen der Zustandsvariablen:

$\ddot{y}(t) = \frac 1 {a_2} \cdot (- a_0 \cdot x_1(t) -a_1 \cdot x_2(t) + b_0 \cdot u(t))$

Die Umwandlung der systembeschreibenden Differenzialgleichung n-ter Ordnung in n-gekoppelte Differenzialgleichungen 1. Ordnung geschieht wie folgt:

Stellt man sich laut dem Blockschaltbild z.B. die Zustandsvariable $x_{1}$ vom Ausgang des Integrators auf den Eingang des gleichen Integrators versetzt vor, dann ist die Ableitung von $x_{1}:\quad {\dot {x}}_{1}={\dot {y}}$ .

Daraus folgen die Zustandsdifferentialgleichungen 1. Ordnung:

${\dot {x}}_{1}={\dot {y}}=x_{2}$

$\dot{x}_2 = \ddot{y} = - \frac {a_0} {a_2} \cdot x_1 - \frac {a_1} {a_2} \cdot x_2 + \frac {b_0} {a_2} \cdot u$

Die Zustandsgrößen $x_{1}\,$ und $x_{2}\,$ bilden den sogenannten Zustandsvektor ${\underline {x}}$ .

Diese Gleichungen werden als Vektordifferenzialgleichungen in Matrizenform wie folgt geschrieben:

${\begin{bmatrix}{\dot {x}}_{{1}}\\{\dot {x}}_{{2}}\\\end{bmatrix}}={\begin{bmatrix}0&1&\\-{\frac {a_{0}}{a_{2}}}&-{\frac {a_{1}}{a_{2}}}&\\\end{bmatrix}}\cdot {\begin{bmatrix}x_{{1}}\\x_{{2}}\\\end{bmatrix}}+{\begin{bmatrix}0\\{\frac {b_{0}}{a_{2}}}\\\end{bmatrix}}\cdot u(t)$

und die Ausgangsgleichung:

${\textbf {y}}(t)={\begin{bmatrix}1&0&\end{bmatrix}}\cdot {\begin{bmatrix}x_{{1}}\\x_{{2}}\\\end{bmatrix}}$

Es existieren verschiedene Signalflusspläne, die zur Lösung der Differenzialgleichung und der Bestimmung der Zustandsvariablen führen. Der Quotient ${\tfrac {1}{a_{2}}}$ kann entsprechend dem Blockschaltbild des Schwingungsglieds links der Subtraktionsstelle liegen, er kann rechts davon liegen, oder die Gleichung kann so umgeformt werden, dass die höchste Ableitung den Koeffizienten 1 hat. Alle diese Maßnahmen führen zu einem gleichen Ergebnis für die Ausgangsgröße y(t). Dies gilt aber nicht für die Definition der Koeffizienten der Zustandsgrößen.

Für Übertragungssysteme mit Polen und Nullstellen gibt es deshalb eine einheitliche Normalform, vorzugsweise die „Regelungsnormalform“ zur Darstellung der Signalflüsse.

Zustandsraummodell

Bei der Zustandsraumdarstellung wird von einem Zustandsraummodell ausgegangen.

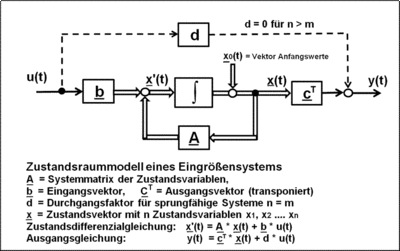
Symbolisches Blockschaltbild eines Modells eines Übertragungssystems in der Zustandsraumdarstellung für ein Eingrößensystem.

Das Blockschaltbild mit dem Signalflussplan des Zustandsraummodells zeigt ein Eingrößen-Übertragungssystem mit einem Eingangssignal u(t) und einem Ausgangssignal y(t) in einer allgemeinen Darstellung für ein lineares Übertragungssystem mit n Differenzialgleichungen 1. Ordnung. Es entspricht der Systemdarstellung der Regelungsnormalform. Anstelle eines Differenzialgleichungssystems n-ter Ordnung tritt eine Ableitung des n-dimensionalen Zustandsvektors 1. Ordnung $\underline \dot x(t)$ . Diese Ableitung ist Eingangsgröße eines Integrators; daraus ergibt sich der Zustandsvektor $\underline x(t)$ .

Die Zustandsgleichungen für die Ableitung des Vektors $\underline \dot x(t)$ und die Ausgangsgröße y(t) eines Eingrößensystems

$\underline{\dot{x}}(t) = \underline {A} \cdot \underline {x}(t) + \underline {b} \cdot u(t)$

$y(t) = \underline {c}^T \cdot \underline {x}(t) + d \cdot u(t)$

können direkt aus dem Blockschaltbild des Zustandsraummodells abgelesen werden.

Das Blockschaltbild des Zustandsraummodells hat eine einheitliche Form, wird aber als Ein- oder Mehrgrößensystem unterschiedlich dargestellt. Bei dem Mehrgrößensystem treten anstelle der skalaren Ein- und Ausgangsgrößen u(t) und y(t) die Vektoren $\underline u(t)$ und $\underline y(t)$ . Die Signalflüsse von Matrizen und Vektoren werden in dem Blockschaltbild durch Doppellinien dargestellt.

Zusammenfassung Zustandsraummodell:

Zustandsraummodell und Blockschaltbild

Das Blockschaltbild mit dem Signalflussdiagramm des Zustandsraummodells ist – abgesehen davon, ob es sich um ein Eingrößensystem oder Mehrgrößensystem handelt – für alle Anwendungen identisch. Es stellt den Signalflussplan der Regelungsnormalform für ein lineares System n-ter Ordnung mit n Differenzialgleichungen erster Ordnung dar. Deshalb benötigt es für die Berechnung des Zustandsvektors $\underline x(t)$ nur einen Integrator.

Das Zustandsraummodell bezieht sich immer auf einen bestimmten Anwendungsfall der Beschreibung eines Übertragungssystems.

Die Wertebeschreibung bezieht sich auf sämtliche Signale des Systems. Dazu gehören die Werte des Systemzustandes $\underline x(t)$ , der Eingangsgröße u(t), die Ausgangsgröße y(t) und die Anfangswerte des Systems $\underline x(0)$ .

Die Signale sind wie im Blockschaltbild dargestellt mit der Systemmatrix, dem Eingangs- und Ausgangsvektor verknüpft. Bei Mehrgrößensystemen wird der einspaltige Eingangsvektor zur Eingangsmatrix, der einzeilige Ausgangsvektor zur Ausgangsmatrix.

Systemmatrix

Die Systemmatrix $\underline A$ enthält die Koeffizienten der Zustandsvariablen. Durch die Anwendung der Normalformen wie die Regelungsnormalform kann die Systemmatrix nach einem relativ einfachen Schema erstellt werden. Die Koeffizienten eines Übertragungssystems n-ter Ordnung stehen bei der Regelungsnormalform in der untersten Zeile der Matrix. Sie können direkt aus der systembeschreibenden Differenzialgleichung oder der zugehörigen Übertragungsfunktion entnommen werden.

Bei Mehrgrößensystemen mit verkoppelten Übertragungsgliedern können die Bestimmung der Zustandsvariablen und die Auslegung der Systemmatrix aufwendig werden. Für jede Ausgangsgröße $y_{1}(t)\cdots y_{r}(t)$ lässt sich eine verkoppelte Übertragungsfunktion bzw. die zugehörige Differenzialgleichung bestimmen. Daraus werden – ggf. nach Linearisierung – die Koeffizienten für die n*n-Systemmatrix $\underline A$ gebildet.

Lineare und nichtlineare Systeme

Das Zustandsraummodell beschreibt lineare Übertragungssysteme durch lineare Differenzialgleichungen bzw. durch Übertragungsfunktionen.

Nichtlineare Übertragungssysteme erfordern einen erhöhten mathematischen Aufwand. Nichtlineare Systeme, z.B. in der Praxis häufig vorkommende mit gebrochener Kennlinie durch Signalbegrenzungen, lassen sich nicht mit linearen Differenzialgleichungen beschreiben. Für sie kommt ebenso wie für Systeme mit Totzeiten die numerische Berechnung zur Anwendung.

Zustandsdifferenzialgleichung und Ausgangsgleichung

Das Zustandsraummodell wird anhand der dargestellten Signalflüsse durch 2 Gleichungen beschrieben, die Zustandsdifferenzialgleichung und die Ausgangsgleichung (auch Ausgabegleichung).

Die Zustandsdifferenzialgleichung ist eine Vektordifferenzialgleichung 1. Ordnung, die die Systemdynamik beschreibt. Sie gibt an, wie das Eingangssignal u(t) die einzelnen Speicher beeinflusst und wie diese Speicher miteinander verkoppelt sind.

Die algebraische Ausgangsgleichung beschreibt, wie das Ausgangssignal y(t) mit den Systemzuständen verbunden ist.

Gleichungen des Zustandsraummodells:

Gleichung	Bei Eingrößensystemen	Bei Mehrgrößensystemen
Zustandsdifferenzialgleichung (auch Zustandsgleichung)	$\underline {{\dot {x}}}(t)=\underline {A}\cdot \underline {x}(t)+\underline {b}\cdot u(t)$	$\underline {{\dot {x}}}(t)=\underline {A}\cdot \underline {x}(t)+\underline {B}\cdot \underline {u}(t)$
Ausgangsgleichung	$y(t) = \underline {c}^T \cdot \underline {x}(t) + d \cdot u(t)$ d = 0 für n > m	$\underline {y}(t) = \underline {C} \cdot \underline {x}(t) + \underline {D} \cdot \underline {u}(t)$ ${\underline {D}}\,$ = 0 für n > m

Bedeutung der Signale und Systemblöcke des Zustandsraummodells:

Bedeutung	Eingrößensystem	Mehrgrößensystem
Ableitung des Zustandsvektors	$\underline {{\dot {x}}}(t)\,$	$\underline {{\dot {x}}}(t)\,$
Zustandsvektor	${\underline {x}}(t)\,$	${\underline {x}}(t)\,$
Zustandsvariable	$x_{i}(t)$	$x_{i}(t)$
Vektor der Anfangsbedingungen	${\underline {x}}_{0}$	${\underline {x}}_{0}$
Eingangssignale	${u}(t)\,$ Eingangsvariable	${\underline {u}}(t)\,$ Eingangsvariablenvektor
Ausgangssignale	${y}(t)\,$ Ausgangsvariable	${\underline {y}}(t)\,$ Ausgangsvariablenvektor
Systemmatrix	${\underline {A}}(t)\,$	${\underline {A}}(t)\,$
Eingangsmatrix	${\underline {b}}(t)\,$ Eingangsvektor	${\underline {B}}(t)\,$ Eingangsmatrix
Ausgangsmatrix	${\underline {c}}^{T}(t)\,$ Ausgangsvektor (transponiert)	${\underline {C}}(t)\,$ Ausgangsmatrix
Durchgangsmatrix	${d}(t)\,$ Durchgangsfaktor = Null für n > m	${\underline {D}}(t)\,$ Durchgangsmatrix = Null für n > m

Indizierung:

Matrizen = Großbuchstaben mit Unterstrich,
Vektoren = Kleinbuchstaben mit Unterstrich,
Transponierte Vektordarstellung, Beispiel: $\underline {k}^{T}\,$

Standardmäßig liegt ein Vektor immer in Spaltenform vor. Um einen Zeilenvektor zu erhalten, muss ein Spaltenvektor transponiert werden.

Lineare Zustandsdifferenzialgleichungen eines Mehrgrößensystems

Laut Fachliteratur werden im Zustandsraum dynamische Systeme allgemein als Mehrgrößensysteme betrachtet. Eingrößensysteme gelten – Im Gegensatz zur klassischen Regelungstechnik – als Sonderfall.

Lineare Übertragungssysteme mit mehreren Eingangs- und Ausgangsgrößen kann man mit linearen Zustandsdifferenzialgleichungen beschreiben.

${\dot {x}}_{1}=a_{{11}}\cdot x_{1}+\cdots +a_{{1n}}\cdot x_{n}+b_{{11}}\cdot u_{1}+\cdots +b_{{1m}}\cdot u_{{m}}$

${\dot {x}}_{2}=a_{{21}}\cdot x_{1}+\cdots +a_{{2n}}\cdot x_{n}+b_{{21}}\cdot u_{1}+\cdots +b_{{2m}}\cdot u_{{m}}$

$\vdots$

${\dot {x}}_{n}=a_{{n1}}\cdot x_{1}+\cdots +a_{{nn}}\cdot x_{n}+b_{{n1}}\cdot u_{1}+\cdots +b_{{nm}}\cdot u_{{m}}$

Die Ausgangsgleichungen bei Linearen Systemen haben folgende Formen:

$y_{1}=c_{{11}}\cdot x_{1}+\cdots +c_{{1n}}\cdot x_{n}+d_{{11}}\cdot u_{1}+\cdots +d_{{1m}}\cdot u_{{m}}$

$y_{2}=c_{21}\cdot x_{1}+\cdots +c_{2n}\cdot x_{n}+d_{21}\cdot u_{1}+\cdots +d_{2m}\cdot u_{m}$

$\vdots$

$y_{r}=c_{r1}\cdot x_{1}+\cdots +c_{rn}\cdot x_{n}+d_{r1}\cdot u_{1}+\cdots +d_{rm}\cdot u_{m}$

Diese in Vektorschreibweise dargestellten Gleichungen kann man auch in Matrizenschreibweise wiedergeben.

Zustandsdifferenzialgleichungen der Mehrgrößensysteme

$\begin{bmatrix} \dot{x}_1(t)\\ \dot{x}_2(t)\\ \vdots\\ \dot{x}_n(t)\\ \end{bmatrix} =\underbrace{\begin{bmatrix} a_{11}& \dots & a_{1n}\\ a_{21}& \dots & a_{2n}\\ \vdots& \ddots &\vdots\\ a_{n1}& \dots & a_{nn}\\ \end{bmatrix}}_{\text{System-Matrix}} \ \cdot \underbrace{\begin{bmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t)\\ \end{bmatrix}}_{\text{Zustd.-Vektor}} + \ \underbrace{\begin{bmatrix} b_{11}& \dots & b_{1m}\\ b_{21}& \dots & b_{2m}\\ \vdots& \ddots &\vdots\\ b_{n1}& \dots & b_{nm}\\ \end{bmatrix}}_{\text{Eingangs-Matrix}} \quad \cdot \underbrace{\begin{bmatrix} u_{1}(t)\\ u_{2}(t)\\ \vdots\\ u_{m}(t)\\ \end{bmatrix}}_{\text{Eing. Gr.-Vektor}}$

Ausgangsgleichungen der Mehrgrößensysteme:

$\begin{bmatrix} y_1(t)\\ y_2(t)\\ \vdots\\ y_r(t)\\ \end{bmatrix} =\underbrace{\begin{bmatrix} c_{11}& \dots & c_{1n}\\ c_{21}& \dots & c_{2n}\\ \vdots& \ddots &\vdots\\ c_{r1}& \dots & c_{rn}\\ \end{bmatrix}}_{\text{Ausgangs-Matrix}} \ \cdot \underbrace{\begin{bmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t)\\ \end{bmatrix}}_{\text{Zustd.-Vektor}} + \ \underbrace{\begin{bmatrix} d_{11}& \dots & d_{1m}\\ d_{21}& \dots & d_{2m}\\ \vdots& \ddots &\vdots\\ d_{r1}& \dots & d_{rm}\\ \end{bmatrix}}_{\text{Durchgangs-Matrix}} \quad \cdot \underbrace{\begin{bmatrix} u_{1}(t)\\ u_{2}(t)\\ \vdots\\ u_{m}(t)\\ \end{bmatrix}}_{\text{Eing. Gr.-Vektor}}$

Lineare Zustandsdifferenzialgleichungen der Eingrößensysteme

Eingrößensysteme haben nur eine Eingangsgröße u(t) und eine Ausgangsgröße y(t) . Dabei gehen die Eingangsmatrizen $\underline {B}$ und Ausgangsmatrizen $\underline {C}$ in den Eingangsvektor $\underline {b}$ und Ausgangsvektor $\underline {c}$ über.

$\begin{bmatrix} \dot{x}_1(t)\\ \dot{x}_2(t)\\ \vdots\\ \dot{x}_n(t)\\ \end{bmatrix} =\underbrace{\begin{bmatrix} a_{11}& \dots & a_{1n}\\ a_{21}& \dots & a_{2n}\\ \vdots& \ddots &\vdots\\ a_{n1}& \dots & a_{nn}\\ \end{bmatrix}}_{\text{System-Matrix}} \ \cdot \underbrace{\begin{bmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t)\\ \end{bmatrix}}_{\text{Zustd.-Vektor}} + \underbrace{\begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix}}_{\text{Eingangs-Vektor}} \cdot \underbrace{\begin{bmatrix} u(t)\\ \end{bmatrix}}_{\text{Eing.-Variable}}$

Ausgangsgleichung der Eingrößensysteme:

$\begin{bmatrix} y(t)\\ \end{bmatrix} =\underbrace{\begin{bmatrix} c_{1}& \dots & c_{n}\\ \end{bmatrix}}_{\text{Ausgangs-Vektor}} \ \cdot \underbrace{\begin{bmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t)\\ \end{bmatrix}}_{\text{Zustd.-Vektor}} + \underbrace{\begin{bmatrix} d\\ \end{bmatrix}}_{\text{Durchg.-Faktor}} \cdot \underbrace{\begin{bmatrix} u(t)\\ \end{bmatrix}}_{\text{Eing.-Variable}}$

Normalformen im Zustandsraum

Bei den Zustandsbeschreibungen mit Normalformen nehmen die Zustandsgleichungen besonders einfache und zweckmäßige Formen für bestimmte Berechnungen an. Für die Normalformen wird von der Systembeschreibung des linearen Übertragungssystems durch die Differenzialgleichung oder zugehörige Übertragungsfunktion ausgegangen.

Zu den bekanntesten Normalformen gehören:

Regelungsnormalform (auch mit Frobenius-Form, Steuerungsnormalform oder 1. Standardform bezeichnet),
Beobachtungsnormalform
Kanonische Normalform

Die Normalformen sind in der Systemmatrix ${\underline {A}}$ durch die örtliche Lage der Koeffizienten erkennbar.

Regelungsnormalform

Die Signalstruktur der Regelungsnormalform stellt sich als ein analoges zeitkontinuierliches System dar, das mit der Eingangsgröße u(t) die Lösung der Differentialgleichung y(t) wiedergibt und gleichzeitig die Zustandsvariablen $x_{1}(t),x_{2}(t)\cdots x_{n}(t)$ zeigt.

Das Blockschaltbild der Regelungsnormalform zeigt die Umsetzung und Lösung der Differenzialgleichung in die physikalischen analogen Signalflüsse der Zustandsgrößen einschließlich der Ausgangsgröße bei gegebener Eingangsgröße. Man kann sie als eine Weiterentwicklung der in der Analogrechentechnik bekannten Verfahren zur Lösung einer Differentialgleichung n-ter Ordnung mit Integratoren betrachten. Die Signalflüsse können bei Kenntnis der Koeffizienten der Zustandsvariablen direkt mittels numerischer Berechnung für beliebige Eingangssignale ermittelt und grafisch dargestellt werden.

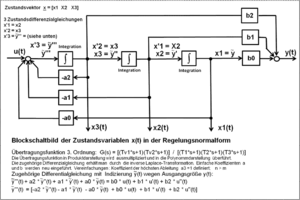
Blockschaltbild des Signalflussplanes eines Übertragungssystems 3. Ordnung in der Regelungsnormalform.

Das vereinfachte Beispiel des Blockschaltbild-Signalflussplanes 2. Ordnung zeigt ein Übertragungssystem, das nur Pole enthält. Für beliebige Systeme mit Polen und Nullstellen in der Regelungsnormalform muss der Signalflussplan um die Ableitungen der Eingangsgröße u(t) so erweitert werden, dass die Terme $b_0 \cdot x_1 + b_1 \cdot x_2 \cdots + b_n \cdot x_{(n+1)}$ sich zu der Ausgangsgröße y(t) addieren.

Übertragungsfunktion und zugehörige Differenzialgleichung in Polynomdarstellung

Die Übertragungsfunktion eines linearen Übertragungssystems in Polynomdarstellung ist definiert als das Verhältnis von Ausgangssignal zu Eingangssignal als Funktion der komplexen Frequenz s. Sie entsteht unter der Voraussetzung, dass die Anfangsbedingungen der Energiespeicher der Ausgangsgröße Y(s) zu Null gesetzt sind:

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}+b_{1}\cdot s+b_{2}\cdot s^{2}+\cdots +b_{m}\cdot s^{m}}{a_{0}+a_{1}\cdot s+a_{2}\cdot s^{2}+\cdots +a_{n}\cdot s^{n}}}$

Dabei bedeuten n = Anzahl der Pole und m = Anzahl der Nullstellen des Systems:

n > m: Dies entspricht dem Normalfall in der Regelungstechnik, d.h. die Anzahl der Pole n sind größer als die der Nullstellen m. Das System ist nicht sprungfähig.
m = n: Diese Beziehung mit gleicher Anzahl der Pole und Nullstellen kommt nur in Ausnahmefällen vor. Das System ist sprungfähig, d.h. eine sprungförmige Änderung der Eingangsgröße wird unverzögert auf den Ausgang übertragen.
m > n: Diese Systeme können nicht mit der Zustandsraumdarstellung behandelt werden. Sie sind auch technisch nicht realisierbar.

Die zugehörige Differenzialgleichung der Übertragungsfunktion ergibt sich durch die inverse Laplace-Transformation.

$a_{n}\cdot y^{{(n)}}(t)+\ \cdots \ +a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)+b_{1}\cdot {\dot {u}}(t)+b_{2}\cdot {\ddot {u}}(t)+\ \cdots \ +b_{m}\cdot u^{{(m)}}(t)$

Der höchste Grad der Ableitung von $y(t)\;$ gibt die Anzahl der Speicherelemente der Strecke wieder.

Blockschaltbild Berechnungsbeispiel der Zustandsvariablen für ein System 3. Ordnung in der Regelungsnormalform.

Zustandsvariablen entstehen aus den Polen des Übertragungssystems

Die Zustandsvariablen eines linearen Systems n-ter Ordnung mit n Energiespeichern entstehen immer aus den Polen. Hat das Übertragungssystem auch Nullstellen – also differenzierende Anteile – so werden die Zustandsvariablen mit den Koeffizienten der Ableitungen der Eingangsgröße u(t) zu der Ausgangsgröße y(t) addiert. Erklärung aus der Systemtheorie: Die Pole einer Übertragungsfunktion bestimmen die Geschwindigkeit der Systembewegung und der Stabilität. Die Nullstellen einer Übertragungsfunktion haben nur Einfluss auf die Amplituden des Systems.

Indizierung der Ableitungen von y(t)

Weil die Ausgangsgröße des Übertragungssystems aber bereits mit y(t) bezeichnet wird, muss die systembeschreibende Differenzialgleichung mit den Ableitungen von y(t) indiziert werden. Die Differentialgleichung erhält anstelle des Symbols y(t) das Symbol ${\tilde y}(t)$ und u(t) durch ${\tilde u}(t)$ eingeführt wird. In der Zustandsraumdarstellung verschwinden die Ableitungen von y(t) und werden durch die Zustandsvariablen x(t) ersetzt.

Damit werden die Zustandsvariablen

$x_{1}(t)={\tilde y}(t)$
$x_{2}(t)={\dot {{\tilde {y}}}}(t)$
$x_{n}(t)={\tilde y}^{{(n-1)}}(t)$

In dem Blockschaltbild der Regelungsnormalform werden die Ableitungen von ${\tilde y}(t)$ durch die Zustandsvariablen $x_{1}\cdots x_{n}$ ersetzt, so dass ${\tilde y}(t)$ nicht mehr in Erscheinung tritt.

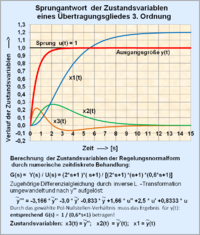
Grafische Darstellung des Verlaufes der Zustandsgrößen und der Ausgangsgröße eines Systems 3. Ordnung mit Polen und Nullstellen nach einem Eingangssprung.

Definition Pol-Nullstellenverhältnis und Koeffizienten der Differenzialgleichung

Die Regelungsnormalform gilt für lineare Systeme mit n Polen und m Nullstellen bis n → m.

Mit Hilfe von numerischen zeitdiskreten Berechnungsmethoden kann die Lösung der Differenzialgleichung y(t) sowie der Verlauf der Zustandsvariablen $x_{1}(t)\cdots x_{n}(t)$ für ein gegebenes Eingangssignal u(t) leicht ermittelt werden.

Die zugehörige Matrizendarstellung für ein in der Regelungstechnik übliches sprungunfähiges System der Ordnung n lautet in der Regelungsnormalform mit folgenden Bedingungen:

Die systembeschreibende Übertragungsfunktion bzw. die zugehörige Differenzialgleichung werden so umgeformt, dass der Koeffizient $a_{n}\,$ der höchsten Ableitung von y(t) gleich 1 entspricht. Sämtliche Koeffizienten werden durch $a_{n}\,$ dividiert und neu geordnet.

Beispiel: Zustandsvariablen für ein Übertragungssystem 4. Ordnung

Die Übertragungsfunktion eines Übertragungssystems z.B. 4. Ordnung (mit den Ableitungen der Eingangsgröße 3. Ordnung) lautet mit der für die Regelungstechnik zulässigen Einschränkung n > m und dem Koeffizient der höchsten Ableitung von y(t): $\ a_{4}=1\,$ :

$G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}+b_{1}\cdot s+b_{2}\cdot s^{2}+b_{3}\cdot s^{3}}{a_{0}+a_{1}\cdot s+a_{2}\cdot s^{2}+a_{3}\cdot s^{3}+s^{4}}}$

Die zugehörige Differenzialgleichung lautet für ein Übertragungssystem 4. Ordnung dann mit den zulässigen Einschränkungen m < n:

$y^{{(4)}}+a_{3}\cdot {y}^{{(3)}}+a_{2}\cdot {\ddot {y}}+a_{1}\cdot {\dot {y}}+a_{0}\cdot y=b_{0}\cdot u+b_{1}\cdot {\dot {u}}+b_{2}\cdot {\ddot {u}}+b_{3}\cdot {u}^{{(3)}}$

Aus der Differenzialgleichung ergeben sich nach bekanntem Schema (Substitution der Ableitungen von y(t) durch x(t)) folgende Zustandsgleichungen:

${\dot {x}}_{{1}}=x_{{2}}$

${\dot {x}}_{{2}}=x_{{3}}$

${\dot {x}}_{{3}}=x_{{4}}$

${\dot {x}}_{{4}}=-a_{{3}}x_{{4}}-a_{{2}}x_{{3}}-a_{{1}}x_{{2}}-a_{{0}}x_{{1}}+u$

$y = b_{0}x_{1} + b_{1}x_{2} + b_{2}x_{3} + b_{3}x_{4}$

Diese Gleichungen können für die Zustandsraumdarstellung in Matrizenschreibweise als Zustandsdifferenzialgleichungen für Eingrößensysteme immer nach gleichem Schema überführt werden:

${\begin{bmatrix}{\dot {x}}_{{1}}(t)\\{\dot {x}}_{{2}}(t)\\{\dot {x}}_{{3}}(t)\\{\dot {x}}_{{4}}(t)\\\end{bmatrix}}=\underbrace {{\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-a_{0}&-a_{1}&-a_{2}&-a_{3}\end{bmatrix}}}_{{{\text{System-Matrix }}\underline {A}}}\quad \cdot \underbrace {{\begin{bmatrix}x_{{1}}(t)\\x_{{2}}(t)\\x_{{3}}(t)\\x_{{4}}(t)\\\end{bmatrix}}}_{{{\text{Zustd.-Vektor}}}}+\underbrace {{\begin{bmatrix}0\\0\\0\\1\\\end{bmatrix}}}_{{{\text{Eingangs-Vektor}}}}\cdot \underbrace {{\begin{bmatrix}u(t)\end{bmatrix}}}_{{{\text{Eing. Gr.-Variable}}}}$

Ausgangsgleichungen für Eingrößensysteme:

${\textbf {y}}(t)=\underbrace {{\begin{bmatrix}b_{0}&b_{1}&b_{2}&b_{3}\end{bmatrix}}}_{{{\text{Ausgangs-Vektor }}\underline {c}^{T}}}\quad \cdot \underbrace {{\begin{bmatrix}x_{{1}}(t)\\x_{{2}}(t)\\x_{{3}}(t)\\x_{{4}}(t)\\\end{bmatrix}}}_{{{\text{Zustds.-Vektor}}}}$

Unter dem Zustandsraummodell in der Regelungsnormalform versteht man eine einheitliche Form der Matrizendarstellung mit folgenden vorteilhaften Eigenschaften:

Die Zählerkoeffizienten der Übertragungsfunktion (Nullstellen) sind nur in dem Ausgangsvektor $\underline {c}^{T}(t)$ enthalten,
Die Nennerkoeffizienten der Übertragungsfunktion (Pole) sind nur in der Systemmatrix ${\underline {A}}$ enthalten,
Die Systemmatrix ${\underline {A}}$ hat eine spezielle Struktur. Von den n·n Elementen sind nur die n-Elemente der letzten Zeile vom Übertragungssystem abhängig,
Der Eingangsvektor $\underline {b}$ ist unabhängig von den Systemeigenschaften.

Steuerbarkeit und Beobachtbarkeit von Übertragungssystemen

Modell eines Übertragungssystems

Für die Analyse, Synthese und Regelung von realen Übertragungssystemen (Regelstrecken), die meist als ein Hardwaresystem vorliegen, ist ein mathematisches Modell des Systems erforderlich.

Modelle in Form von Differenzialgleichungen beschreiben das zeitliche Verhalten des Systems exakt. Sind diese Differenzialgleichungen oder zugehörigen Übertragungsfunktionen nicht gegeben, kann das zeitliche Verhalten eines Hardwaresystems durch experimentelle Identifizierungsmaßnahmen (Experimentelle Systemidentifikation) mit Hilfe von Testsignalen ermittelt werden.

Bei der prinzipiellen Vorgehensweise wird der Identifikationsalgorithmus für die Modellparameter solange verändert, bis für ein gegebenes Eingangssignal u(t) die Differenz der Ausgangsgrößen y(t) − y_Modell(t) innerhalb eines beliebigen Zeitablaufs des gemessenen Originalausgangs mit dem Modellausgang annäherungsweise verschwindet.

Das Modell legt die Struktur eines Signalflussplanes fest, aus dem die Zustandsgrößen abgeleitet werden können. Hat das System n Energiespeicher, so werden die n Zustandsgrößen durch den Zustandsgrößenvektor ${\underline {x}}$ zusammengefasst. Sind die Eingangsgröße u(t) und die Koeffizienten der Zustandsgrößen der Strecke bekannt, kann die Ausgangsgröße y(t) errechnet werden.

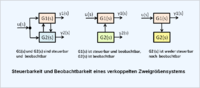
Blockschaltbild einfacher Modelle zur Verdeutlichung der Begriffe Steuerbarkeit und Beobachtbarkeit.

Das Übertragungssystem (Regelstrecke) muss steuerbar sein. Alle Zustandsvariablen müssen verfügbar sein. Pol- Nullstellenkompensation im Zustandsraum ist nicht erlaubt, weil ein Informationsverlust eintritt.

Während bei Eingrößensystemen sich das Problem der Steuerbarkeit und der Beobachtbarkeit nicht immer stellt, weil Eingrößensysteme sich einfacher darstellen, ist bei verkoppelten Mehrgrößensystemen gegebenenfalls eine Prüfung nach bekannten Regeln der Steuerbarkeitsmatrix und der Beobachtbarkeitsmatrix erforderlich.

Steuerbarkeit Eingrößensystem: Für ein System mit nur einer Steuergröße u(t) wird aus der Matrix ${\underline {B}}$ ein Spaltenvektor $\underline {b}$ .

Beobachtbarkeit Eingrößensystem: Für ein System mit nur einer Ausgangsgröße y(t) wird aus der Matrix ${\underline {C}}$ ein Zeilenvektor ${\underline {c}}^{T}$

Damit ergibt sich eine vereinfachte Steuerbarkeitsmatrix und eine vereinfachte Beobachtbarkeitsmatrix.

Steuerbarkeit

Bei der Zustandsregelung werden alle Zustandsgrößen auf den Eingang des Systems zurückgeführt. Für die Durchführung einer Zustandsregelung müssen alle Zustandsvariablen zur Verfügung stehen. Diese Bedingung ist erfüllt, wenn die Stellgröße des Reglers auf alle Zustandsvariablen wirkt.

Ein System ist steuerbar, wenn es von einem beliebigen Anfangszustand nach endlicher Zeit in einen beliebigen Endzustand gebracht werden kann.

Allgemein gilt für die Steuerbarkeit auf die Signalgrößen bezogen:

Ein System ist vollständig zustandssteuerbar, wenn für jede Anfangszeit $t_{0}$ jeder Anfangszustand $\underline x_0(t)$ nach endlicher Zeit durch einen unbeschränkten Steuervektor ${\underline {u}}(t)$ in jeden beliebigen Endzustand ${\underline {x}}$ gebracht werden kann.

Ein System n-ter Ordnung ist dann vollständig zustandssteuerbar, wenn die Steuerbarkeitsmatrix ${\underline {Q}}_{S}$ den Rang hat.

${\underline {Q}}_{S}={\bigg [}\ {\underline {B}}\ |\ {\underline {A}}{\underline {B}}\ |\ {\underline {A}}^{2}{\underline {B}}\ |...|\ {\underline {A}}^{n-1}{\underline {B}}\ {\bigg ]}$

Sind alle Zustände (Zustandsgrößen) eines Systems steuerbar, so ist auch das System steuerbar.

Beobachtbarkeit / Beobachter

Zustandsregelungen erfordern alle Zustandsgrößen eines Übertragungssystems. Die Zustandsgrößen werden durch Messung aus der Regelstrecke ermittelt. Ist dieser Fall gegeben, entspricht dies der „vollständigen Beobachtbarkeit“.

Häufig können aus technischen oder kommerziellen Gründen nicht alle Zustandsvariablen gemessen werden. Deshalb werden einzelne nicht messbare Zustandsvariablen aus den bekannten und vorhandenen Eingangs- und Ausgangsgrößen der Regelstrecke errechnet. Zustandsbeobachter, die diese Aufgabe durchführen, sind zusätzliche Regelsysteme. Sie rekonstruieren Zustandsvariable aus dem Verlauf der Ein- und Ausgangsgrößen an einem Modell der Regelstrecke. Die Eingangsvariable u(t) muss bekannt sein.

Zustandsbeobachter können nur realisiert werden, wenn das zu beobachtende System beobachtbar ist, was bei den allermeisten technischen Regelstrecken der Fall ist.

Ein lineares Übertragungssystem ist beobachtbar, wenn durch Messung der Ausgangsvariablen y(t) der Anfangszustand des Zustandsvektors $\underline x_0$ nach endlicher Zeit bestimmt werden kann.

Ein System heißt vollständig beobachtbar, wenn jeder Anfangszustand $\underline x(t_{0})$ aus den Messungen des Ausgangssignals y(t) in einem bestimmten Zeitintervall ab $t_{0}$ exakt bestimmt werden kann.

Ein System n-ter Ordnung ist dann vollständig beobachtbar, wenn die Beobachtbarkeitsmatrix ${\underline {Q}}_{B}$ den Rang hat.

${\underline {Q}}_{B}={\begin{bmatrix}{\underline {C}}\\{\underline {C}}{\underline {A}}\\{\underline {C}}{\underline {A}}^{2}\\{\underline {C}}{\underline {A}}^{3}\\\vdots \\{\underline {C}}{\underline {A}}^{n-1}\end{bmatrix}}$

Zustandsregler mit Beobachter

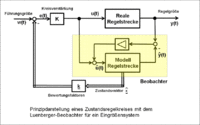
Prinzipbild eines Zustandsreglers mit Beobachter für ein Eingrößensystems.

Für die Realisierung des Zustandsbeobachters wird das Separationsprinzip angewandt. Es erlaubt den getrennten Entwurf der Zustandsrückführung und der Beobachtung. Ein solches Verfahren kann mit dem „Luenberger-Beobachter“ realisiert werden. Dabei sind die Regelstrecke und der Beobachter mit der Modell-Regelstrecke parallel am Eingang u(t) geschaltet. Der Ausgang beider Systeme $y(t)-{\hat y}(t)$ wird überwacht und zur Korrektur der Modell-Regelstrecke verwendet.

Der Beobachter benötigt ein möglichst genaues Modell der Regelstrecke.

Durch die Struktur der Regelstrecke und durch Identifikationsverfahren mittels der Sprung- oder Impulsantwort der Regelstrecke kann ein Modell der Regelstrecke gebildet werden, das in den meisten Fällen noch mit kleinen Fehlern behaftet ist.

Nach dem Verfahren mit dem Luenberger-Beobachter wird der Regelstrecken-Ausgang y(t) mit dem Modellausgang ${\hat y}(t)$ verglichen und über eine Regelschleife auf den Eingang des Modells additiv zurückgeführt, so dass der Ausgang der Regelstrecke und der Ausgang des Modells innerhalb einer Ausregelzeit identisch sind. Es wird davon ausgegangen, dass der unbekannte Zustandsvektor ${\underline {x}}$ und der ermittelte Modell-Zustandsvektor $\underline {{\hat x}}$ dann nahezu identisch sind.

Für den Zustandsregelkreis wird der ermittelte Zustandsvektor $\underline {{\hat x}}$ mit Bewertungsfaktoren $\underline k$ für das gewünschte dynamische Verhalten des Zustandsregelkreises von der Führungsgröße w(t) subtrahiert.

Regelung im Zustandsraum

Bei einschleifigen Standardregelkreisen wird üblicherweise die Ausgangsgröße y(t) des Regelkreises von der Führungsgröße w(t) subtrahiert und dann als Regeldifferenz $e(t)=w(t)-y(t)$ dem Regler zugeführt. Dieses Verfahren bezeichnet man im Zusammenhang mit der Behandlung von Systemen im Zustandsraum als Ausgangsrückführung.

Eine übliche Regler-Entwurfsstrategie für Regelstrecken mit Ausgangsrückführung ist relativ einfach:

Durch Pol-Nullstellenkompensation von Regler und Regelstrecke des offenen Regelkreises wird die Übertragungsfunktion des Gesamtregelkreises vereinfacht, d.h. die Ordnung der Differentialgleichung der Regelstrecke wird reduziert, in dem die Werte der Nullstellen des Reglers auf die Werte des Pols der Strecke gesetzt werden. Ein I-Anteil des Reglers vermeidet eine bleibende Regelabweichung, fügt aber einen zusätzlichen Pol hinzu. Zu optimierender Parameter ist die Kreisverstärkung . Die Sprungantwort der Regelgröße verläuft als Funktion von asymptotisch bis stark überschwingend bis zum Erreichen des Sollwertes.

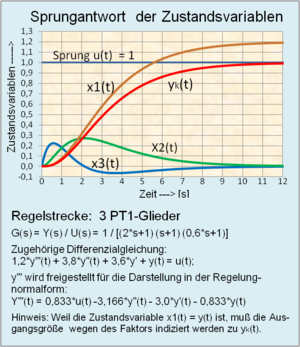
Sprungantwort der Zustandsvariablen einer PT3-Regelstrecke.

Die Zustandsvariablen eines mathematischen Modells einer Regelstrecke können aus einer gewöhnlichen systembeschreibenden Differentialgleichung bestimmt werden. Grundlage der Lösung der Differenzialgleichung ist der Signalflussplan mit der grafischen Darstellung der Regelungsnormalform. Dabei werden die Terme der Ableitungen der Ausgangsgröße y(t) jeweils integriert und mit den zugehörigen Koeffizienten auf den Systemeingang zurückgeführt.

Für jede Ableitung y(t) wird die Bezeichnung der Zustandsgrößen x(t) wie folgt eingeführt:

$x_{1}(t)=y(t)$

$x_{2}(t)={\frac {dy}{dt}}={\dot {y}}$

$x_{3}(t)={\ddot {y}}$

$x_{n}(t)={\frac {d^{(n-1)}y}{dt^{(n-1)}}}=y^{(n-1)}(t)$

Der zeitliche Verlauf der Zustandsvariablen als Folge eines Eingangssprungs $u(t)=1$ an dem Modell zeigt den Vorteil der Behandlung des Systems im Zustandsraum gegenüber einer klassischen „Ausgangsrückführung“ des Systems. Die Zustandsvariablen x(t) erscheinen zeitlich früher als die Ausgangsgröße y(t) . Dieses Verhalten wird beim Zustandsregelkreis genutzt, indem die Zustandsvariablen auf eine Soll-Ist-Differenz mit der Führungsgröße w(t) zurückgeführt werden.

Zustandsregler

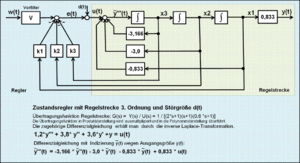
Blockschaltbild eines Zustandsreglers für eine Regelstrecke 3. Ordnung eines Eingrößensystems.

Simulationen eines Zustandsregelkreises können mit einem guten Modell der Regelstrecke an einem programmierbaren Rechner einfach durchgeführt werden. Die Beschreibung des Signalflussplanes der Regelstrecke und des Reglers im Zustandsraum kann sowohl in Form von Matrizen als auch mit Differenzengleichungen erfolgen. Je nach Höhe der Ordnung der Differenzialgleichung werden alle Zustandsgrößen einem Zustandsregler zugeführt, der auf den Eingang des Zustandsraummodells der Regelstrecke wirkt. Durch die Rückführung sämtlicher Zustandsvariablen entsteht ein mehrschleifiger Regelkreis.

Der lineare Zustandsregler bewertet die einzelnen Zustandsvariablen der Regelstrecke mit Faktoren und summiert die so entstandenen Zustandsprodukte zu einem Soll-Istwert-Vergleich.

$u(t)=w(t)-x_{1}\cdot k_{1}-x_{2}\cdot k_{2}-\cdots -x_{n}\cdot k_{n}=w(t)-\underline x(t)\cdot \underline k(t)\,$

Es handelt sich bei diesem Zustandsregler nicht um einen P-Regler, wenngleich ein solcher Eindruck laut Signalflussplan entstehen könnte. Durch die mit dem Regler zurückgeführten Zustandsvariablen mit Bewertungsfaktoren durchlaufen noch einmal die Rechenschaltung zur Lösung der Differenzialgleichung mit n Integratoren und bilden neue Kreisvariablen, wodurch differenzierendes Verhalten entsteht. Deshalb entspricht die Wirkung der zurückgeführten Zustandsgrößen je nach Höhe der Ordnung der Differenzialgleichung der Strecke der eines $PD_{{(n-1)}}$ -Reglers.

Als Entwurfsstrategie für die Bestimmung der Bewertungsfaktoren des Zustandsreglers gilt die Polzuweisung (Polvorgabe) des geschlossenen Regelkreises.

Auch empirische Einstellungen eines Modellregelkreises sind leicht möglich. Durch die Hintereinanderschaltung der Integratoren ist nur die Zustandsvariable $x_{1}(t)=y(t)$ eine stationäre Größe, wenn die Eingangsgröße u(t) konstant ist. Alle anderen Zustandsvariablen – eine stabile Regelstrecke vorausgesetzt – streben gegen den Wert Null. Nach Einstellung und Optimierung des Faktors $k_{1}$ ergibt sich ein stabiler Regelkreis bestimmter Dämpfung mit einem Proportionalfehler der Regelgröße y(t) gegenüber w(t) . Die anderen Faktoren der Zustandsvariablen werden hintereinander z.B. zur Optimierung des Übergangsverhaltens eingestellt.

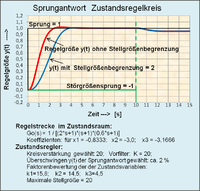
Sprungantwort der Regelgröße y(t) eines Zustandsregelkreises mit und ohne Stellgrößenbegrenzung.

Ein Vorfilter vor dem Soll-Ist-Vergleich korrigiert den statischen Fehler zwischen w(t) und y(t) .

Voraussetzung zur Rückführung der Zustandsvariablen:

Die Regelstrecke muss steuerbar sein.
Alle Zustandsvariablen müssen verfügbar sein. Pol- Nullstellenkompensation im Zustandsraum ist nicht erlaubt, weil Informationsverlust.

In der Praxis können die Zustandsvariablen an einer Regelstrecke gemessen werden, was nicht immer möglich ist. Abhilfe geben Beobachter durch Rekonstruktion der Zustandsvariablen, wenn die Strecke beobachtbar ist.

Theoretisch entsprechen n Zustandsvariablen eines Systems den Ausgängen der -fachen Differentiation der Ausgangsgröße y(t)

. Wegen der zur Realisierung unvermeidlichen parasitären Zeitkonstanten und Verstärkung des Signalrauschens kann dieser Weg nicht beschritten werden.

Mit dem Zustandsregler ergeben sich folgende regelungstechnischen Eigenschaften eines Regelkreises:

Dynamisches Verhalten

Zum Vergleich: Sprungantwort eines Regelkreises mit Ausgangsrückführung und PD2-Regler.

Weil die Signalinformationen der Zustandsvariablen der Regelstrecke frühzeitiger zur Verfügung stehen als bei der Ausgangsrückführung, ist das dynamische Verhalten des Regelkreises günstiger, als ein Regelkreis mit Ausgangsrückführung. Mit einem Zustandsregler lassen sich hohe Anforderungen an die Regelgüte erfüllen.

Differenzieren durch Integrieren

In dem Zustandsregelkreis wird durch die Rückführung der Zustandsvariablen durch Integrationen differenziert. Die mit einer Differentiation verbundenen Nachteile wie parasitäre Zeitkonstanten und Signalrauschen treten nicht auf. Ebenso treten keine großen Stellgrößen bei Sprüngen des Eingangssignals auf.

Zustandsvariable $x_{1}(t)$ im stationären Zustand

Im stationären Zustand des Zustandsregelkreises zeigt nur die Zustandsvariable $x_{1}$ einen stationären Wert. Alle anderen (n-1)

-Zustandsvariablen haben wegen der Hintereinanderschaltung der Integratoren den Wert Null.

Verhalten der Regelgröße

Die Ausgangsgröße (Regelgröße) y(t)

wird beim Zustandsregler nicht erfasst. Hat die Regelstrecke keine Nullstellen (differenzierende Anteile), dann ist zu jeder Zeit $t\to 0$ die Zustandsvariable $x_{1}$ proportional y(t)

. Sie unterscheiden sich durch den Koeffizienten $b_{0}$ .

Liegen Nullstellen in der Regelstrecke vor, dann hat die Ausgangsgröße y(t)

während der Einschwingzeit (nichtstationärer Zustand) ein anderes Zeitverhalten als die Zustandsvariable $x_{1}$ .

Verhalten der Regelgröße bei Störgrößen

Je nach Angriffsort der Störgrößen treten unerwünschte Eigenschaften auf. Die Störung am Ausgang der Regelstrecke wird nicht erfasst. Die Störgröße an anderen Teilen der Regelstrecke wird nur durch die Kreisverstärkung reduziert aber nicht gegen Null geregelt. Letzteres gilt in gleicher Weise für jeden Regelkreis, in dem kein I-Verhalten enthalten ist.

Vorfilter

Durch die Zustandsrückführung kann keine stationäre Genauigkeit der Regelgröße zum Sollwert erreicht werden. Selbst bei einer Regelstrecke ohne Nullstellen, also ohne differenzielle Anteile, ist die Zustandsvariable $x_{1}$ nach der Regelungsnormalform nicht identisch mit der Ausgangsgröße y(t). Deshalb wird die Zustandsrückführung häufig mit einem Vorfilter erweitert. Die Führungsgröße w(t)

wirkt direkt auf das Vorfilter. Für einfache Anforderungen kann mittels eines Faktors in dem Vorfilter eine Korrektur durchgeführt werden, damit im stationären Zustand $w(t)=y(t)$ erreicht wird.

Der Zustandsregler in der dargestellten Eigenschaft dient dem Verständnis seiner Vorteile. Er erlaubt in seinem Verhalten als PD-Regler eine höhere Kreisverstärkung als in einem Regelkreis mit einer Ausgangsrückführung. Dabei ist innerhalb des Zustandsregelkreises keine differenzierende Komponente enthalten.

In einem Vergleich mit einem Standard-PD2-Regler und Ausgangsrückführung und sonst gleicher Kreisdämpfung, gleicher Regelstrecke und Störgröße ergeben sich für diesen Regler erhebliche Nachteile wie riesige Stellgrößen, sehr schlechte Störunterdrückung und bei Stellgrößenbegrenzungen auf $>2$ ( $=200\,\%$ ) totzeitähnliches Allpassverhalten.

Je nach Anforderung hinsichtlich Regelabweichung und Störunterdrückung am Ausgang der Regelstrecke kann er im Vergleich zu einem konventionellen PID-Standardregler unterlegen sein. Abhilfe dieser Nachteile schafft ein mit einem PI-Regler überlagerter Regelkreis. Damit hat der Zustandsregler die erheblich besseren Eigenschaften.

Der Einsatz der Zustandsregler hängt letztlich von einer Kosten-Nutzen-Bewertung ab.

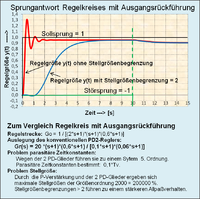
Zustandsregler mit überlagertem Regelkreis

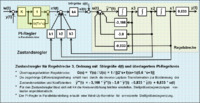
Blockschaltbild eines Zustandsreglers mit überlagertem PI-Regelkreis für eine Regelstrecke 3. Ordnung eines Eingrößensystems.

Für anspruchsvolle Regelaufgaben mit Systemen im Zustandsraum kann die Einführung eines überlagerten Regelkreises für den Zustandsregelkreis mit einer Ausgangsrückführung erforderlich sein. Damit sind sämtliche stationären Probleme für die Übereinstimmung der Führungsgröße mit der Regelgröße und konstante Störanteile ausgeschaltet.

Es empfiehlt sich der Einsatz eines PI-Reglers. Laut der Übertragungsfunktion des PI-Reglers in der Produktdarstellung besteht der Regler aus den Komponenten I-Glied und PD-Glied. Dieser Regler lässt nur eine vorübergehende Regelabweichung zu, vorausgesetzt, die Führungsgröße und eine mögliche Störgröße sind konstant. Durch die PD-Komponente kann ein Verzögerungsanteil (PT1-Glied) des Zustandsregelkreises kompensiert werden. Signalrauschen des PD-Gliedes wird durch das I-Glied reduziert.

Für die Auslegung des überlagerten PI-Zustandsregelkreises sind folgende Parameter zu beachten:

Sprungantwort eines Zustandsregelkreises mit einem überlagerten PI-Regler und Stellgrößenbegrenzung.

Stellgrößen

Große Stellgrößen im Regelkreis machen eine Regelstrecke schnell, sofern die Stabilität des Kreises nicht gefährdet ist. In vielen Fällen begrenzt die Regelstrecke eine große Stellgröße. Damit wird eine Sprungantwort im Großsignalverhalten verzögert und verzerrt. Dieses Problem tritt meistens bei Einsatz von P- und PD-Reglern auf. Dennoch bedeutet eine hohe P-Kreisverstärkung im Kleinsignalverhalten, dass die Regelabweichung geringer und die Störunterdrückung größer werden.

Bewertung der Faktoren der Zustandskoeffizienten

Die Faktoren $k_{1}\cdots k_{n}\,$ der zurückgeführten Zustandsvariablen, die Kreisverstärkung und die Vorhaltezeit $T_{v}$ des PD-Anteils des PI-Reglers bestimmen die Dynamik des Zustandsregelkreises. Sie sind alle voneinander abhängig.

Zustandsvariable $x_{1}$ im stationären Zustand

Stationär bestimmt die Zustandsvariable $x_{1}$ die Ausgangsgröße y(t)

. Alle anderen Zustandsvariablen haben den Wert Null. Der überlagerte Regelkreis führt die Regelgröße y(t)

auf das Niveau der Führungsgröße w(t)

, vorausgesetzt w(t)

ist konstant.

Störgröße

Die Größe der P-Kreisverstärkung bestimmt die dynamische Reduzierung angreifender Störgrößen im Bereich der Regelstrecke. Im stationären Zustand hat eine konstante Störgröße wegen des I-Anteils des überlagerten Regelkreises keinen Einfluss.

Ein Zustandsregler mit überlagertem PI-Regelkreis hat gegenüber einem konventionellen gut optimierten Regelkreis mit jeweils gleicher Regelstrecke und gleichem Einschwingverhalten eindeutige dynamische Vorteile.

Vorteile:

Eine höhere Kreisverstärkung erlaubt eine bessere Störunterdrückung,
die Stellgrößen sind bei der Sprungantwort für einen gegebenen Grenzwert der Überschwingung kleiner,
keine parasitäre Zeitkonstante des Reglers erforderlich,
das Vorfilter entfällt,
die Signal-Rauschanteile sind im überlagerten Zustands-Regelkreis gering, weil keine Differenzierung beim PI-Regler vorkommt.

Nachteile allgemein:

Die Zustandsgrößen stehen meistens nicht zur Verfügung. Sie müssen gemessen werden.
Evtl. müssen die Zustandsgrößen durch einen Beobachter rekonstruiert werden.
Wie bei allen Reglern mit I-Anteil erfolgt im Falle der Begrenzung durch die Regelstrecke bei der Sprungantwort ein überhöhtes Überschwingen der Regelgröße. Durch eine Wind-Up-Korrektur wird dieser Effekt kompensiert.
Erhöhter Materialaufwand, speziell geschultes Fachpersonal erforderlich.

Mathematisches Konzentrat der Regeln und Gleichungen im Zustandsraum

Beschreibung linearer Systeme

Zeitkontinuierliche lineare Systeme werden durch die lineare Differentialgleichung n-ter Ordnung

$y^{{(n)}}+\ldots +d_{{1}}y^{{(1)}}+d_{{0}}y=n_{{m}}u^{{(m)}}+\ldots +n_{{1}}u^{{(1)}}+n_{{0}}u$

beschrieben. Falls die Koeffizienten $d_{{i}}$ und $n_{{k}}$ alle konstant sind, ist die Laplace-Transformation ausführbar und es gilt die Übertragungsfunktion

$G(s)={\frac {n_{{m}}s^{{m}}+\ldots +n_{{1}}s+n_{{0}}}{s^{{n}}+d_{{n-1}}s^{{n-1}}+\ldots +d_{{1}}s+d_{{0}}}}$ .

Eine Differentialgleichung n-ter Ordnung kann in ein System von n Differentialgleichungen 1. Ordnung

${\dot x}_{1}=a_{{1,1}}x_{1}+\ldots +a_{{1,n}}x_{n}+b_{1}u$

$\ldots$

${\dot x}_{n}=a_{{n,1}}x_{1}+\ldots +a_{{n,n}}x_{n}+b_{n}u$

überführt werden.

Zeitdiskrete lineare Systeme werden durch die lineare Differenzengleichung n-ter Ordnung

$a_{n}y(k+n)+a_{{n-1}}y(k+n-1)+\ldots +a_{1}y(k+1)+a_{0}y(k)=$

$b_{m}u(k+m)+\ldots +b_{1}u(k+1)+b_{0}u(k)$

beschrieben. Falls die Koeffizienten $a_{i}$ und $b_{j}$ alle konstant sind, ist die z-Transformation ausführbar und es gilt die Übertragungsfunktion

$G(z)={\frac {b_{m}z^{m}+b_{{m-1}}z^{{m-1}}+\ldots +b_{1}z+b_{0}}{a_{n}z^{n}+a_{{n-1}}z^{{n-1}}+\ldots +a_{1}z+a_{0}}}$ .

Eine Differenzengleichung n-ter Ordnung kann in ein System von n Differenzengleichungen 1. Ordnung

$x_{1}(k+1)=a_{{1,1}}x_{1}(k)+\ldots +a_{{1,n}}x_{n}(k)+b_{1}u(k)$

$\ldots$

$x_{n}(k+1)=a_{{n,1}}x_{1}(k)+\ldots +a_{{n,n}}x_{n}(k)+b_{n}u(k)$

überführt werden.

Lineare Zustandsgleichungen

Signalflussplan Zustandsraum

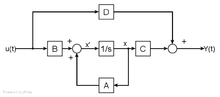
Für zeitkontinuierliche Systeme lauten die linearen Grundgleichungen in vektorieller Form:

${\dot {{\mathbf {x}}}}={\mathbf {A}}{\mathbf {x}}+{\mathbf {B}}{\mathbf {u}}$

${\mathbf {y}}={\mathbf {C}}{\mathbf {x}}+{\mathbf {D}}{\mathbf {u}}$

Über die Matrizen $\mathbf {A}$ und $\mathbf {B}$ sind die Verkettungen der einzelnen Zustände, samt die Zugriffe über die Steuervariablen (Eingangsgrößen) $\mathbf {u}$ darstellbar. Die Matrix $\mathbf {A}$ wird als Systemmatrix, $\mathbf {B}$ als Steuermatrix bezeichnet. Die Beobachtungsmatrix ${\mathbf {C}}$ beschreibt die Auswirkungen des Systems auf den Ausgang. Die Durchgangsmatrix $\mathbf{D}$ beschreibt die Durchgriffe des Systems, sie ist bei nicht sprungfähigen Systemen Null.

Einen wichtigen Sonderfall stellen Systeme mit einer Ein- und einer Ausgangsgröße dar (SISO Single Input, Single-Output Systeme). Hier sind $\mathbf {B}$ und ${\mathbf {C}}$ Vektoren und $\mathbf{D}$ ein Skalar. Es werden dann häufig die Formelzeichen $\mathbf{b}$ , ${\mathbf {c}}^{\top }$ und ${\mathbf {d}}$ verwendet.

In vielen Fällen interessiert anstelle eines kontinuierlichen Verlaufs nur der Systemzustand zu diskreten Zeitpunkten, beispielsweise den Abtastzeitpunkten bei Regelung durch einen Digitalrechner. In diesem Fall ist ${\mathbf {x}}(t)$ anstelle einer vektorwertigen Funktion der Zeit eine Folge ${\mathbf {x}}(k)$ von Vektoren. An die Stelle der Zustandsdifferentialgleichung tritt dann eine Differenzengleichung.

Die Typen der linearen Grundgleichungen:

System-Typ	Zustandsraum-Modell
Kontinuierlich Zeitinvariant	${\dot {{\mathbf {x}}}}(t)={\mathbf {A}}{\mathbf {x}}(t)+{\mathbf {B}}{\mathbf {u}}(t)$ ${\mathbf {y}}(t)={\mathbf {C}}{\mathbf {x}}(t)+{\mathbf {D}}{\mathbf {u}}(t)$
Kontinuierlich Zeitvariant	${\dot {{\mathbf {x}}}}(t)={\mathbf {A}}(t){\mathbf {x}}(t)+{\mathbf {B}}(t){\mathbf {u}}(t)$ ${\mathbf {y}}(t)={\mathbf {C}}(t){\mathbf {x}}(t)+{\mathbf {D}}(t){\mathbf {u}}(t)$
Diskret Zeitinvariant	${\mathbf {x}}(k+1)={\mathbf {A_{d}}}{\mathbf {x}}(k)+{\mathbf {B_{d}}}{\mathbf {u}}(k)$ ${\mathbf {y}}(k)={\mathbf {C}}{\mathbf {x}}(k)+{\mathbf {D}}{\mathbf {u}}(k)$
Diskret Zeitvariant	${\mathbf {x}}(k+1)={\mathbf {A_{d}}}(k){\mathbf {x}}(k)+{\mathbf {B_{d}}}(k){\mathbf {u}}(k)$ ${\mathbf {y}}(k)={\mathbf {C}}(k){\mathbf {x}}(k)+{\mathbf {D}}(k){\mathbf {u}}(k)$
Laplace-Transformierte Kontinuierlich Zeitinvariant	$s{\mathbf {X}}(s)={\mathbf {A}}{\mathbf {X}}(s)+{\mathbf {B}}{\mathbf {U}}(s)$ ${\mathbf {Y}}(s)={\mathbf {C}}{\mathbf {X}}(s)+{\mathbf {D}}{\mathbf {U}}(s)$
Z-Transformierte Diskret Zeitinvariant	$z{\mathbf {X}}(z)={\mathbf {A_{d}}}{\mathbf {X}}(z)+{\mathbf {B_{d}}}{\mathbf {U}}(z)$ ${\mathbf {Y}}(z)={\mathbf {C}}{\mathbf {X}}(z)+{\mathbf {D}}{\mathbf {U}}(z)$

Für die letzten beiden Fälle wurde davon ausgegangen, dass der Anfangszustand des Systems ${\mathbf {x}}(0)=0$ ist (siehe Differentiationssatz der Laplace-Transformation bzw. Differenzensatz der Z-Transformation).

Die zeitdiskrete Zustandsdarstellung wird aus der kontinuierlichen Form mittels Diskretisierung über einer festen Zeitschrittweite T in der Form

${\mathbf {A_{d}}}=e^{{{\mathbf {A}}T}}$

${\mathbf {B_{d}}}=\int _{0}^{T}e^{{{\mathbf {A}}\tau }}{\mathbf {B}}d\tau$

gewonnen. Gilt $\vert {\mathbf {A}}\vert \neq 0$ ergibt das Integral

${\mathbf {B_{d}}}={\mathbf {A}}^{{-1}}(e^{{{\mathbf {A}}T}}-{\mathbf {I}}){\mathbf {B}}$ .

Die diskrete Form ist besonders für Berechnungen in Echtzeit geeignet. In Echtzeit wird zuerst die Ausgangsgleichung gerechnet, und danach erst die Zustandsdifferenzengleichung zur Ermittlung der Zustände für den nächsten Berechnungsschritt. Die zeitkontinuierliche Darstellung eignet sich hingegen gut für Simulationen ohne Echtzeit-Ansprüche, durch numerische Integration. Die Exaktheit kann hier durch die Wahl des Integrationsverfahrens und die Anpassung der statischen oder dynamischen Schrittweite beeinflusst werden.

Von zentraler Bedeutung ist die Systemmatrix, aus der die Eigenwerte, und damit die Systemdynamik und deren Stabilität abgeleitet werden kann (charakteristisches Polynom). Ist die Durchgriffsmatrix keine Nullmatrix, haben die Systemeingänge zeitgleichen Einfluss auf die Ausgänge, was zu einer algebraischen Schleife führen kann.

Sind A, B, C, D konstant, so ist das System linear und zeitinvariant, d.h. ein sog. LZI-System.

Nichtlineare Zustandsgleichungen

Ein nichtlineares System n-ter Ordnung kann als ein System nichtlinearer Differenzialgleichungen 1. Ordnung

${\dot x}_{1}=f_{1}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))$

$\ldots \vdots \ldots$

${\dot x}_{n}=f_{n}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))$

oder kompakter in Vektorschreibweise

${\dot {{\mathbf {x}}}}={\mathbf {f}}({\mathbf {x}}(t),{\mathbf {u}}(t))$

geschrieben werden.

Für den Ruhepunkt $({\mathbf {{\tilde x}}},{\mathbf {{\tilde u}}})$ gilt

${\mathbf {f}}({\mathbf {{\tilde x}}},{\mathbf {{\tilde u}}})={\mathbf {0}}$

Ist ${\mathbf {x^{*}}}(t)$ die Abweichung des Systems vom Ruhepunkt, dann gilt

${\mathbf {x}}(t)={\mathbf {{\tilde x}}}+{\mathbf {x^{*}}}(t)$

${\mathbf {u}}(t)={\mathbf {{\tilde u}}}+{\mathbf {u^{*}}}(t)$

und

${\mathbf {{\dot x}}}={\mathbf {{\dot x}^{*}}}$ .

Die linearisierte Darstellung ${\mathbf {{\dot x}^{*}}}={\mathbf {A}}{\mathbf {x^{*}}}(t)+{\mathbf {B}}{\mathbf {u^{*}}}(t)$

mit den Jacobi-Matrizen $\mathbf{A} = \left.\frac{\mathbf{df}}{\mathbf{dx}}\right|_{\mathbf{x}=\mathbf{\tilde x},\mathbf{u}=\mathbf{\tilde u}}$ und $\mathbf{B} = \left.\frac{\mathbf{df}}{\mathbf{du}}\right|_{\mathbf{x}=\mathbf{\tilde x},\mathbf{u}=\mathbf{\tilde u}}$ ergibt sich aus einer mehrdimensionalen Taylor-Entwicklung um den Ruhepunkt linearisiert.

Ähnlichkeitstransformation

Die Zustandsraumdarstellung ist nicht eindeutig. Zum gleichen System existieren unendlich viele Zustandsraumdarstellungen. Anstatt der gewohnten Zustandsvariablen $\mathbf {x}$ kann man auch einen neuen Satz an Zustandsvariablen ${\mathbf {z}}$ benutzen, falls man ${\mathbf {z}}$ durch $\mathbf {x}$ beschreiben kann. ${\mathbf {z}}={\mathbf {P}}{\mathbf {x}}$ , wobei $\mathbf{P}$ eine reguläre, lineare Transformationsmatrix ist, d.h. ${\mathbf {z}}$ muss durch $\mathbf {x}$ ohne Hinzufügen von Eingängen oder Ableitungen beschreibbar sein.

Es gilt dann: $\{{\mathbf {A}},{\mathbf {B}},{\mathbf {C}},{\mathbf {D}}\}\to \{{\mathbf {PAP}}^{{-1}},{\mathbf {PB}},{\mathbf {CP}}^{{-1}},{\mathbf {D}}\}$

Die neue Zustandsraumdarstellung beschreibt das gleiche System. Es ist deshalb selbstverständlich, dass alle Systemeigenschaften bei der Transformation unverändert bleiben.

Übertragungsfunktion

Die „Übertragungsfunktion“ eines kontinuierlichen zeitinvarianten Zustandsraum-Modells kann bei verschwindenden Anfangsbedingungen (x(0)=0) auf folgende Weise hergeleitet werden:

${\dot {{\mathbf {x}}}}(t)={\mathbf {A}}{\mathbf {x}}(t)+{\mathbf {B}}{\mathbf {u}}(t)$

durch die Laplace-Transformation erhält man

$s{\mathbf {X}}(s)={\mathbf {A}}{\mathbf {X}}(s)+{\mathbf {B}}{\mathbf {U}}(s)$

$(s{\mathbf {I}}-{\mathbf {A}}){\mathbf {X}}(s)={\mathbf {B}}{\mathbf {U}}(s)$

${\mathbf {X}}(s)=(s{\mathbf {I}}-{\mathbf {A}})^{{-1}}{\mathbf {B}}{\mathbf {U}}(s)$

womit ${\mathbf {X}}(s)$ in der Ausgangs-Gleichung substituiert wird

${\mathbf {Y}}(s)={\mathbf {C}}{\mathbf {X}}(s)+{\mathbf {D}}{\mathbf {U}}(s)$

${\mathbf {Y}}(s)={\mathbf {C}}((s{\mathbf {I}}-{\mathbf {A}})^{{-1}}{\mathbf {B}}{\mathbf {U}}(s))+{\mathbf {D}}{\mathbf {U}}(s)$

und die Übertragungsfunktion ergibt

${\mathbf {Y}}(s)={\mathbf {G}}(s){\mathbf {U}}(s)$

${\mathbf {G}}(s)={\mathbf {C}}(s{\mathbf {I}}-{\mathbf {A}})^{{-1}}{\mathbf {B}}+{\mathbf {D}}$

Hierbei entspricht $\mathbf {I}$ der Einheitsmatrix.

Allgemeine Lösung im Zeitbereich

Die allgemeine Lösung im Zeitbereich erhält man mit den Startwerten ${\textstyle \mathbf {x_{0}} =\mathbf {x} (t_{0})}$ durch:

$\mathbf {x} (t)=e^{\mathbf {A} (t-t_{0})}\mathbf {x_{0}} +\int _{t_{0}}^{t}{e^{\mathbf {A} (t-\tau )}\mathbf {Bu} (\tau )}d\tau$

$\mathbf {y} (t)=\mathbf {C} e^{\mathbf {A} (t-t_{0})}\mathbf {x_{0}} +\mathbf {C} \int _{t_{0}}^{t}{e^{\mathbf {A} (t-\tau )}\mathbf {Bu} (\tau )}d\tau +\mathbf {Du} (t)$

Schwierigkeiten kann dabei die Matrixexponentialfunktion bereiten, die analog zur skalaren Exponentialfunktion definiert ist durch die Potenzreihe

$e^{{{\mathbf {A}}t}}=I+{\mathbf {A}}t+{\frac {1}{2!}}({\mathbf {A}}t)^{2}+{\frac {1}{3!}}({\mathbf {A}}t)^{3}+\cdots$

Um hier einen geschlossenen Ausdruck angeben zu können, ist es hilfreich, $\mathbf {A}$ mittels Hauptachsentransformation auf Diagonalgestalt zu transformieren. Für eine Diagonalmatrix der Form

$\Lambda =\operatorname {diag}(\lambda _{1},\ldots ,\lambda _{n})$

ergibt sich dann die Matrixexponentialfunktion zu

$e^{{\Lambda t}}=\operatorname {diag}(e^{{\lambda _{1}t}},\ldots ,e^{{\lambda _{n}t}})$

Normalformen

Normalformen werden benutzt, um strukturelle Eigenschaften eines Systems klar hervorzuheben. Oft besitzt ein System in der Zustandsraumdarstellung Zustandsvariablen, welche sich im Übertragungsverhalten des Systems nicht bemerkbar machen. So kann es z.B. sein, dass sich Pole und Nullstellen kürzen, sodass diese keinerlei Einfluss auf die Übertragungsfunktion G(s) haben. Diesen Fall nennt man eine Nichtminimal-Realisierung des Systems, und dies führt dazu, dass das System entweder nicht steuerbar, nicht beobachtbar, oder weder steuerbar noch beobachtbar ist.

Regelungsnormalform

Signalflussplan Regelungsnormalform

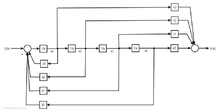
Die gegebene Übertragungsfunktion kann mit folgendem Ansatz in eine Zustandsraumdarstellung überführt werden.

Die gegebene Übertragungsfunktion wird in die Zähler- und Nennerfaktoren ausmultipliziert

${\textbf {G}}(s)={\frac {n_{{3}}s^{{3}}+n_{{2}}s^{{2}}+n_{{1}}s+n_{{0}}}{s^{{4}}+d_{{3}}s^{{3}}+d_{{2}}s^{{2}}+d_{{1}}s+d_{{0}}}}$ .

Zu dieser Übertragungsfunktion im Frequenzbereich gehört im Zeitbereich die Differentialgleichung (DGL):

$y^{{(4)}}+d_{{3}}y^{{(3)}}+d_{{2}}y^{{(2)}}+d_{{1}}y^{{(1)}}+d_{{0}}y=n_{{3}}u^{{(3)}}+n_{{2}}u^{{(2)}}+n_{{1}}u^{{(1)}}+n_{{0}}u\,$

Aus dieser DGL ergeben sich für die ZR – Darstellung nach Regelungsnormalform folgende Zustandsgleichungen:

${\dot {x}}_{{1}}=x_{{2}}$

${\dot {x}}_{{2}}=x_{{3}}$

${\dot {x}}_{{3}}=x_{{4}}$

$\dot{x}_{4} = -d_{3}x_{4} -d_{2}x_{3} -d_{1}x_{2} -d_{0}x_{1} + u$

$y = n_{0}x_{1} + n_{1}x_{2} + n_{2}x_{3} + n_{3}x_{4}\,$

Die Koeffizienten können nun einfach direkt in die Zustandsmatrizen eingetragen werden:

${\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\\{\dot {x}}_{4}\\\end{bmatrix}}={\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-d_{0}&-d_{1}&-d_{2}&-d_{3}\end{bmatrix}}\cdot {\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\\end{bmatrix}}+{\begin{bmatrix}0\\0\\0\\1\\\end{bmatrix}}\cdot u(t)$

$\mathbf {y} (t)={\begin{bmatrix}n_{0}&n_{1}&n_{2}&n_{3}\end{bmatrix}}\cdot {\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\\\end{bmatrix}}$

Die Transformationsmatrix folgt aus der Steuerbarkeitsmatrix

$Q_{s}={\begin{pmatrix}B&A\cdot B&A^{2}\cdot B&A^{3}\cdot B\end{pmatrix}}$ .

Wenn $\operatorname{det} Q_s \not = 0$ ist das System steuerbar. Dann kann aus

$q_{s}={\begin{pmatrix}0&0&0&1\end{pmatrix}}\cdot Q_{s}^{{-1}}$

die Transformationsmatrix

$P=T_{R}={\begin{pmatrix}q_{s}\\q_{s}\cdot A\\q_{s}\cdot A^{2}\\q_{s}\cdot A^{3}\end{pmatrix}}^{{-1}}$

gebildet werden.

Beobachtungsnormalform

Signalflussplan Beobachtungsnormalform

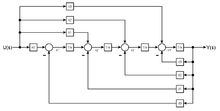
Die Differenzialgleichung nach $y^{{(4)}}\,$ aufgelöst

$y^{(4)} = n_{3}u^{(3)} - d_{3}y^{(3)} + n_{2}u^{(2)} - d_{2}y^{(2)} + n_{1}u^{(1)} - d_{1}y^{(1)} + n_{0}u - d_{0}y \,$

und 4-mal integriert ergibt

$y=\int (n_{{3}}u-d_{{3}}y)dt+\int \int (n_{{2}}u-d_{{2}}y)dt^{2}+\int \int \int (n_{{1}}u-d_{{1}}y)dt^{3}+\int \int \int \int (n_{{0}}u-d_{{0}}y)dt^{4}$ .

Daraus lassen sich die Zustandsgrößen

${\dot {x}}_{{1}}=-d_{0}y+n_{0}u$

$\dot{x}_{2} = x_1 -d_1y+n_1u$

$\dot{x}_{3} = x_2 -d_2y+n_2u$

$\dot{x}_{4} = x_3 -d_3y+n_3u$

und die Ausgangsgleichung

$y=x_{4}\,$

ableiten. Einsetzen von ergibt

${\dot {x}}_{{1}}=-d_{0}x_{4}+n_{0}u$

${\dot {x}}_{{2}}=-d_{1}x_{4}+x_{1}+n_{1}u$

${\dot {x}}_{{3}}=-d_{2}x_{4}+x_{2}+n_{2}u$

${\dot {x}}_{{4}}=-d_{3}x_{4}+x_{3}+n_{3}u$ .

oder in Matrix-Form

${\begin{bmatrix}{\dot {x}}_{{1}}\\{\dot {x}}_{{2}}\\{\dot {x}}_{{3}}\\{\dot {x}}_{{4}}\\\end{bmatrix}}={\begin{bmatrix}0&0&0&-d_{0}\\1&0&0&-d_{1}\\0&1&0&-d_{2}\\0&0&1&-d_{3}\end{bmatrix}}*{\begin{bmatrix}x_{{1}}\\x_{{2}}\\x_{{3}}\\x_{{4}}\\\end{bmatrix}}+{\begin{bmatrix}n_{0}\\n_{1}\\n_{2}\\n_{3}\\\end{bmatrix}}*u(t)$

${\textbf {y}}(t)={\begin{bmatrix}0&0&0&1\end{bmatrix}}*{\begin{bmatrix}x_{{1}}\\x_{{2}}\\x_{{3}}\\x_{{4}}\\\end{bmatrix}}$

Die Transformationsmatrix folgt aus der Beobachtbarkeitsmatrix

$Q_{b}={\begin{pmatrix}C\\C\cdot A\\C\cdot A^{2}\\C\cdot A^{3}\end{pmatrix}}$

Wenn $\operatorname{det} Q_b \not = 0$ ist das System beobachtbar. Dann kann aus

$q_{b}=Q_{b}^{{-1}}\cdot {\begin{pmatrix}0&0&0&1\end{pmatrix}}^{T}$

die Transformationsmatrix

$P=T_{B}={\begin{pmatrix}q_{b}&A\cdot q_{b}&A^{2}\cdot q_{b}&A^{3}\cdot q_{b}\end{pmatrix}}^{{-1}}$

gebildet werden.

Kanonische Normalform

Signalflussplan Diagonalform

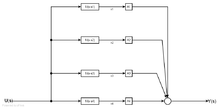
Hat die Übertragungsfunktion G(s) einfache, reelle Polstellen s_k kann eine Partialbruchzerlegung der Form

$G(s)=\sum _{{k=1}}^{4}{\frac {A_{k}}{s-s_{k}}}$

durchgeführt werden. Aus

$X_{k}(s)={\frac {1}{s-s_{k}}}U(s)$

ergeben sich durch Rücktransformation die Zustandsgleichungen

${\dot x}_{k}=s_{k}x_{k}+u$

und die Ausgangsgröße

$y=\sum _{{k=1}}^{4}A_{k}x_{k}$ .

In Matrizenschreibweise

${\begin{bmatrix}{\dot {x}}_{{1}}\\{\dot {x}}_{{2}}\\{\dot {x}}_{{3}}\\{\dot {x}}_{{4}}\\\end{bmatrix}}={\begin{bmatrix}s_{1}&0&0&0\\0&s_{2}&0&0\\0&0&s_{3}&0\\0&0&0&s_{4}\end{bmatrix}}*{\begin{bmatrix}x_{{1}}\\x_{{2}}\\x_{{3}}\\x_{{4}}\\\end{bmatrix}}+{\begin{bmatrix}1\\1\\1\\1\\\end{bmatrix}}*u(t)$

und

${\textbf {y}}(t)={\begin{bmatrix}A_{1}&A_{2}&A_{3}&A_{4}\end{bmatrix}}*{\begin{bmatrix}x_{{1}}\\x_{{2}}\\x_{{3}}\\x_{{4}}\\\end{bmatrix}}$

Die Zustandsgleichungen sind in diesem Fall entkoppelt. Die Transformationsmatrix wird aus den zu den Eigenwerten s_k der Systemmatrix gehörenden Eigenvektoren ${\textbf {v}}_{k}$ in der Form

$P=T_{D}={\begin{pmatrix}{\textbf {v}}_{0}&{\textbf {v}}_{1}&{\textbf {v}}_{2}&{\textbf {v}}_{3}\end{pmatrix}}$

geschrieben.

Siehe auch

Systemtheorie (Ingenieurwissenschaften)

Basierend auf einem Artikel in:

Wikipedia.de