Kleinsignalverhalten

Das Kleinsignalverhalten beschreibt das Verhalten eines Systems bei Aussteuerung mit kleinen Signalen, wobei das Wort „klein“ nicht als geringer Abstand zum Nullpunkt, sondern zu einem Arbeitspunkt zu verstehen ist. Für diese Kleinsignale erreicht man in einem beschränkten, aber für die Aufgabe wesentlichen Bereich ein näherungsweise lineares Übertragungsverhalten zwischen Eingangs- und Ausgangssignal.

Linearität ist zum Beispiel Voraussetzung für die Anwendung der Laplace-Transformation in der Systemtheorie/Elektrotechnik zwecks Systemanalyse.

Anwendungsgebiet

Die Beschreibung mittels des Kleinsignalverhaltens wird angewendet bei nichtlinearen Bauelementen und analog-elektronischen Schaltungen, die Transistoren oder andere nichtlineare Halbleiterbauteile enthalten. Die Arbeitspunkte der Bauteile werden dabei so gewählt, dass weder die Grenzen des Aussteuerbereiches noch stärker nichtlineare Bereiche der Übertragungskennlinie erreicht werden. Durch eine kleine Aussteuerung um den Arbeitspunkt herum ergibt sich näherungsweise ein linearer Zusammenhang zwischen der Eingangs- und der Ausgangsgröße.

Jede Nichtlinearität erzeugt Verzerrung. Es entstehen Oberschwingungen, was gleichbedeutend mit einer Steigerung des Klirrfaktors ist. Die Grenze für das Kleinsignalverhalten ergibt sich aus der Grenze, wie weit die Verzerrung akzeptiert werden kann.

Lineare Näherung

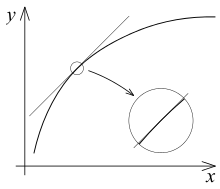
Die nichtlineare Kennlinie und ihre Tangente unterscheiden sich in einen kleinen Bereich um den Berührpunkt nur geringfügig

Eine stetig gekrümmte Kennlinie kann in einem willkürlich gewählten Arbeitspunkt durch ihre Tangente in diesem Punkt linear angenähert werden. Solange das Verhalten des Bauteils durch die Tangente beschreibbar ist, spricht man von seinem Kleinsignalverhalten.

Bei bekannter Übertragungs-Funktion kann man diese durch eine Taylorreihe approximieren. Da man beim Kleinsignalverhalten nur lineare Anteile berücksichtigt, bricht man die Reihenentwicklung um den Arbeitspunkt A nach dem linearen Glied ab.

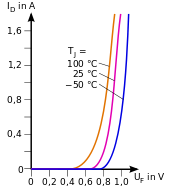
Kennlinie der Diode 1N4001 im Durchlassbereich

Beispiel Diode

Die Strom-Spannungs-Kennlinie einer Silizium-Halbleiterdiode im Durchlassbereich (für den Diodenstrom $I_\mathrm D$ bei positiver Spannung $U_\mathrm F$ ) lässt sich im Wesentlichen durch die Shockley-Gleichung beschreiben.

$I_\mathrm D = I_\mathrm S\, \left( \mathrm e^\frac{U_\mathrm F}{n\,U_\mathrm T} - 1 \right) \approx I_\mathrm S \cdot \mathrm e^\frac{U_\mathrm F}{n \, U_\mathrm T}\ .$

Der lineare Taylor-Ansatz

$f(x)\ \approx\ f(a)\ +\ f'(a)\ \cdot\ (x-a)$

ergibt in dieser Anwendung

$I_\mathrm D \approx I_\mathrm{D,A} + \left. \frac{\mathrm dI_\mathrm D}{\mathrm d U_\mathrm F} \right|_{U_\mathrm{F,A}} \cdot\left( U_\mathrm F - U_\mathrm{F,A} \right)$

und nach dem Einsetzen und Differenzieren

$I_\mathrm D \approx I_\mathrm{D,A} + I_\mathrm S\cdot \mathrm e^{\frac{U_\mathrm{F,A}}{n\, U_\mathrm T}} \frac1{n \,U_\mathrm T} \left( U_\mathrm F - U_\mathrm{F,A} \right) = I_\mathrm{D,A} + \frac{I_\mathrm{D,A}}{n \, U_\mathrm T} \left( U_\mathrm F - U_\mathrm{F,A} \right)\ .$

Für die Kleinsignalgrößen $u = U_\mathrm F - U_\mathrm{F,A}$ und $i = I_\mathrm D - I_\mathrm{D,A}$ erhält man

$i\approx \frac{I_\mathrm{D,A}}{n\, U_\mathrm T}\,u \ .$

Damit entspricht das Kleinsignalverhalten einer Diode dem eines differenziellen Widerstands, dessen Wert r=u/i umgekehrt proportional zur Stromstärke im Arbeitspunkt ist.

Basierend auf einem Artikel in:

Wikipedia.de