Phasenporträt

Phasenporträt einer Differentialgleichung im $\mathbb {R} ^{2}$

Potentielle Energie und Phasenporträt eines einfachen Pendels

Phasenporträt nahe einem typischen hyperbolischen Fixpunkt, einem Sattelpunkt

Beim van-der-Pol-Oszillator laufen alle Trajektorien auf einen Grenzzyklus zu, was sich anhand von Beispieltrajektorien innerhalb und außerhalb des Zyklus illustrieren lässt.

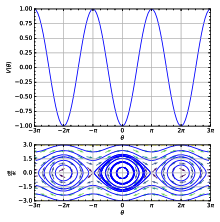
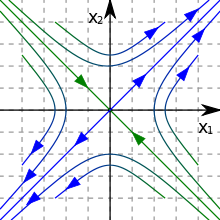
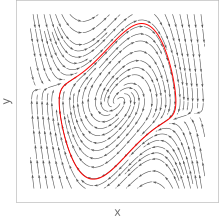
In der Mathematik dient das Phasenporträt (auch Phasenportrait) der Veranschaulichung einer autonomen Differentialgleichung. Das Phasenraumporträt gibt eine Möglichkeit, die zeitlichen Entwicklungen dynamischer Systeme graphisch zu analysieren. Dazu werden nur die dynamischen Gleichungen des Systems benötigt, eine explizite Darstellung der Zeitentwicklung, etwa durch analytisches Lösen einer Differentialgleichung, ist nicht nötig.

Das Phasenporträt besteht aus der Gesamtheit aller Orbits des dynamischen Systems, zusammen mit Pfeilen, die die zeitliche Entwicklung entlang der Orbits angeben. Da die Gesamtheit aller Orbits der gesamte Phasenraum des dynamischen Systems ist, zeichnet man nur einige charakteristische Orbits. Aus dem Phasenporträt eines dynamischen Systems lässt sich ein erster Eindruck über sein globales Verhalten gewinnen, beispielsweise die Existenz und Stabilität von Fixpunkten und periodischen Orbits. Aus Gründen der Übersichtlichkeit ist meist nur das Zeichnen von Phasenporträts in $\mathbb {R}$ und $\mathbb {R} ^{2}$ sinnvoll.

Man betrachtet also eine Differentialgleichung erster Ordnung:

$x'=f(x,y)$

$y'=g(x,y)$

mit $F=(f,g):U\to \mathbb {R} ^{2}$ für eine Teilmenge $U\subset \mathbb{R} ^{2}$ . Die einzige Information, die wir über die gesuchte Bahn (x(t),y(t)) haben, ist ihre Ableitung $(x^{\prime }(t),y^{\prime }(t))$ , die an der Stelle durch $F(x(t),y(t))$ gegeben ist. Die Funktion ordnet also jedem Element aus dem Definitionsbereich eine Steigung oder auch Richtung zu. Trägt man diese Richtungen in Form von Geradenstücken F(x,y) an den zugehörigen Punkten (x,y) ein, wird ein Muster sichtbar. Die Lösungen der Differentialgleichung sind Kurven, die tangential zu diesen Geradenstücken stehen und als Bahnkurven oder Trajektorien bezeichnet werden. Die Menge aller Bahnkurven, bzw. Trajektorien, gibt das Phasenporträt.

Für ein Raster von Punkten wird die Richtung der Bewegung im Phasenraum durch Pfeile dargestellt; so wird ein Vektorfeld eingezeichnet. Folgt man nun ausgehend von einem bestimmten Startpunkt dem Pfeil, kommt man zu einem neuen Punkt, wo man dieses Vorgehen wiederholen kann. So kann man anhand des Vektorfelds zusätzlich typische Trajektorien in das Phasenraumporträt einzeichnen, die das qualitative Verhalten der zeitlichen Entwicklung einzuschätzen helfen. Für einfache dynamische Systeme kann man Vektorfeld und Beispieltrajektorien oft mit der Hand einzeichnen, bei komplexeren Systemen kann dies durch Computerprogramme geschehen.

Basierend auf einem Artikel in:

Wikipedia.de