I-Glied

I-Glied im Strukturbild

I-Glied als Symbol

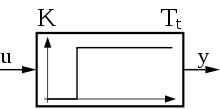
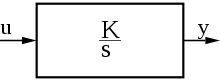
Als I-Glied bezeichnet man ein LZI-Übertragungsglied in der Regelungstechnik, das ein integratives Übertragungsverhalten aufweist. D.h., die Änderungsgeschwindigkeit der Ausgangsgröße wird von der Höhe der Amplitudenänderung der Eingangsgröße bestimmt.

Die zugehörige Funktionalbeziehung im Zeitbereich lautet

$y(t)=K\int _{0}^{t}u(\tau )\,{\mathrm {d}}\tau$ bzw. auch ${\dot y}(t)=K\cdot u(t)$ ,

so dass die komplexe Übertragungsfunktion im Bildbereich die Form

$G(s)={\frac {K}{s}}$

$T_{I}={\frac {1}{K}}$

hat. Hierbei bezeichnet K, K > 0, die Übertragungskonstante bzw. den Verstärkungsfaktor des I-Gliedes, oder T_I die Integrationszeit.

Wird das I-Glied als Teil eines PID-Reglers verwendet, ist es für die Ausregelung zuständig, d.h., es besitzt keine bleibende Regelabweichung. Das I-Glied kann aber auch Teil der Regelstrecke sein, beispielsweise bei Geschwindigkeit als Eingangsgröße und Position als Ausgangsgröße. In diesem Fall muss das Reglerkonzept die Umkehrung der Integration (normalerweise durch ein D-Glied) vorsehen.

Bodediagramm

Beim I-Glied ist $G(j\omega )={\frac {K}{j\omega }}$ . Daher gilt für den Amplituden- und Phasengang im Bodediagramm:

$|G(j\omega )|={\frac {K}{\omega }}$

$\varphi (\omega )=-{\frac {\pi }{2}}$

Die Betragskennlinie ist also eine Gerade, die mit 20 dB/Dekade fällt und bei ω = 1 den Wert K_dB hat. Die Phasenkennlinie ist konstant −90°.

Bodediagramm eines I-Gliedes (K = 2)

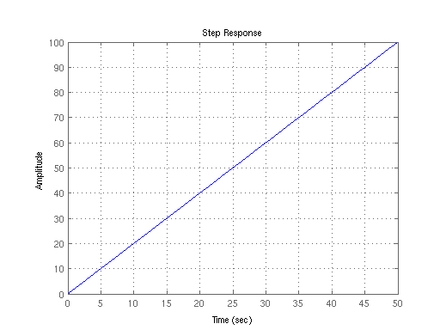
Sprungantwort

Die Sprungantwort des I-Gliedes beschreibt eine Gerade mit der Steigung ${\frac {\Delta y}{\Delta t}}=K$ .

Sprungantwort eines I-Gliedes (K = 2)

Ortskurve

Die Ortskurve ( $0\leq \omega \leq \infty$ ) des I-Gliedes verläuft für K > 0 auf der imaginären Achse, kommend von $-j\infty$ bei $\omega = 0$ und endend im Nullpunkt für $\omega \to \infty$ .

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de