
Nullstelle
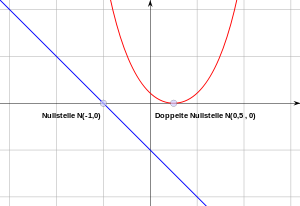
Nullstelle ist ein Begriff der Mathematik im Zusammenhang mit Funktionen.
Definition
Nullstellen sind bei einer Funktion diejenigen Werte der Ausgangsmenge (des
Definitionsbereichs
),
bei denen das im Rahmen der Abbildung zugeordnete Element der Zielmenge (des Wertebereichs
)
die Null ist (
).
In der mathematischen Praxis sind das oft Funktionen vom Typ
mit
oder
mit
Bei der Darstellung einer Funktion
als Graph in einem kartesischen
Koordinatensystem (
)
sind das also Punkte des Graphen auf der
-Achse,
bei an dieser Stelle stetigen
Funktionen also Schnitt- oder Berührungspunkte.
Nullstellen von Polynomfunktionen werden auch als Wurzeln bezeichnet.
Nullstellen reellwertiger Funktionen
Definition
Ein Element
der Definitionsmenge
einer Funktion
heißt Nullstelle von
,
wenn
gilt. Man sagt dann auch:
hat eine Nullstelle bei
,
oder
verschwindet an der Stelle
Beispiel
3 und −3 sind Nullstellen der Funktion ,
denn
und
.
0 ist keine Nullstelle, denn .
Mehrfache Nullstellen
Definitionen
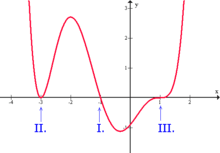
Ist
stetig (z.B. eine Polynomfunktion) und an der Nullstelle
differenzierbar, so kann man die Nullstelle
„herausteilen“. Genauer: Es gibt eine in
stetige Funktion
,
sodass
für alle
.
Es gibt dann zwei Fälle:
. In diesem Fall nennt man
eine einfache Nullstelle.
, d. h. auch
hat in
eine Nullstelle. Oder anders ausgedrückt: Auch nachdem man die Nullstelle
aus
herausgeteilt hat, bleibt
immer noch eine Nullstelle. In diesem Fall nennt man
eine mehrfache Nullstelle von
.
Um zu bestimmen, ob
eine einfache oder eine mehrfache Nullstelle ist, benutzt man die Tatsache, dass
der Wert
gleich der Ableitung von
an der Stelle
ist. Für eine differenzierbare Funktion
bekommt man also folgendes Kriterium:
- Eine Nullstelle
von
ist genau dann eine mehrfache Nullstelle, wenn
ist.
Falls
öfter differenzierbar ist, dann kann man diesen Prozess wiederholen. Man
definiert:
Es sei
eine natürliche
Zahl. Eine (mindestens)
-mal
differenzierbare
Funktion
auf einer offenen Teilmenge
hat in
eine (mindestens)
-fache
Nullstelle oder eine Nullstelle der Ordnung (mindestens)
,
wenn
selbst und die ersten
Ableitungen
von
an der Stelle
den Wert Null annehmen:
Sei
nun mindestens
-mal
differenzierbar. Ist
eine
-fache
Nullstelle, aber keine
-fache,
also
so nennt man
die Ordnung oder Vielfachheit der Nullstelle.
Beispiel
mit den Ableitungen
.
Es gilt ,
also ist
eine Nullstelle von
.
Weiter gilt
aber
Somit ist 1 eine dreifache, aber keine vierfache Nullstelle von ,
also eine Nullstelle der Vielfachheit 3.
Weitere Eigenschaften
- Eine Funktion
hat genau dann eine
-fache Nullstelle bei
, wenn
eine Nullstelle und
eine
-fache Nullstelle bei
hat.
- Eine
-mal stetig differenzierbare Funktion
hat genau dann eine mindestens
-fache Nullstelle bei
, wenn es eine stetige Funktion
gibt, sodass
-
und
- gilt.
- Eine
-mal stetig differenzierbare Funktion
hat genau dann bei
eine Nullstelle der Vielfachheit
, wenn es eine stetige Funktion
gibt, sodass
-
und
- gilt.
- Die Funktion
hat bei 0 eine Nullstelle der Ordnung unendlich und ist daher nicht analytisch.
Existenz und Berechnung von Nullstellen
Aus dem Zwischenwertsatz
kann man oft indirekt die Existenz einer Nullstelle erschließen: Ist von zwei
Funktionswerten ,
einer stetigen
Funktion einer positiv und einer negativ, so hat
mindestens eine Nullstelle zwischen
und
.
(Anschaulich gesprochen muss der Funktionsgraph,
der die beiden Punkte
und
verbindet, die
-Achse
schneiden.)
Je nach Funktion kann es schwer oder unmöglich sein, die Nullstellen explizit zu bestimmen, d.h. die Gleichung
nach
aufzulösen. In diesem Fall kann man Näherungswerte für Nullstellen mithilfe
verschiedener numerischer
Verfahren, beispielsweise der Bisektion
(Intervallhalbierungsverfahren), der Regula
falsi oder einer geeigneten Fixpunktiteration
für stetige Funktionen, des Newton- oder Halley-Verfahrens für
differenzierbare Funktionen, des Weierstraß-(Durand-Kerner)-Verfahrens
oder des Bairstow-Verfahrens
für Polynome bestimmen.
Nullstellen von Polynomfunktionen
Ist
ein Ring
und
ein Polynom
über
,
so heißt ein Element
Nullstelle von
,
wenn die Einsetzung von
in
Null ergibt:
Ist
ein Ringhomomorphismus, so können analog Nullstellen von
in
definiert werden.
Mithilfe der Polynomdivision
kann man zeigen, dass
genau dann eine Nullstelle von
ist, wenn
durch
teilbar ist, d.h., wenn es ein Polynom
gibt, sodass
gilt. Diese Aussage wird manchmal auch Nullstellensatz genannt; es besteht jedoch Verwechslungsgefahr mit dem hilbertschen Nullstellensatz.
Eine -fache
Nullstelle oder Nullstelle der Ordnung
ist ein Element
,
sodass
durch
teilbar ist. Man nennt
auch die Vielfachheit oder Multiplizität der Nullstelle.
Bestimmung der Nullstellen von Polynomen kleinen Grades
Für Polynome über einem Körper, deren Grad höchstens vier ist, gibt es allgemeine Lösungsformeln mit Radikalen, um die Nullstellen direkt zu bestimmen:
- Grad 1: Siehe lineare
Gleichung. Das Polynom
hat die Nullstelle
.
- Grad 2: Siehe quadratische Gleichung.
- Grad 3: Siehe kubische Gleichung.
- Grad 4: Siehe quartische Gleichung.
Polynome mit ganzzahligen Koeffizienten
Ist
ein Polynom mit ganzzahligen Koeffizienten, so ist jede ganzzahlige Nullstelle
ein Teiler von
.
Aus dem Lemma
von Gauß folgt: Ist
ein normiertes Polynom mit ganzzahligen Koeffizienten, so ist jede rationale
Nullstelle ganzzahlig und damit ein Teiler von
.
Beispiel:
Die Teiler
des Absolutglieds von
sind keine Nullstellen, also hat
keine rationale Nullstelle. Da jede Faktorisierung von
einen Linearfaktor enthalten müsste, folgt daraus, dass
über
irreduzibel
ist.
Polynome mit reellen Koeffizienten
Polynome ungeraden Grades über den reellen Zahlen haben stets mindestens eine reelle Nullstelle; das folgt aus dem Zwischenwertsatz. Eine andere Begründung (sofern man den Fundamentalsatz der Algebra bereits zur Verfügung hat) ist die folgende: Echt komplexe Nullstellen reeller Polynome treten stets als Paare komplex konjugierter Zahlen auf. Polynome geraden bzw. ungeraden Grades haben also stets gerade bzw. ungerade viele reelle Nullstellen, wenn man jede Nullstelle entsprechend ihrer Vielfachheit zählt. Eine Anwendung des letzteren Prinzips stellt das numerische Bairstow-Verfahren dar.
Beispiel:
Das Polynom
hat die Nullstelle
,
die sich als Teiler des Absolutgliedes leicht erraten lässt. Damit erhält man
durch Polynomdivision
woraus sich noch die beiden zueinander komplex konjugierten Nullstellen
und
ergeben.
Polynome mit ausschließlich reellen Nullstellen
Ist
ein Polynom, dessen Nullstellen alle reell sind, so liegen diese in dem
Intervall mit den Endpunkten
Beispiel:
Das Polynom
hat die vier reellen Nullstellen −3, −2, −1 und 1. Nutzung der Intervallsformel
ergibt
.
Gerundet ergibt sich das Intervall
- I = [−3,812; 1,312].
Die Nullstellen befinden sich also im gefundenen Intervall.
Für
geht die Formel über in die bekannte p-q-Formel.
Polynome mit komplexen Koeffizienten
Der Fundamentalsatz der Algebra besagt: Jedes nichtkonstante Polynom über den komplexen Zahlen hat mindestens eine Nullstelle. Indem man wiederholt Linearfaktoren zu Nullstellen abspaltet, erhält man die Aussage, dass sich jedes Polynom
über den komplexen Zahlen in der Form
schreiben lässt. Dabei sind
die verschiedenen Nullstellen von
und
ihre jeweiligen Vielfachheiten.
Polynome über vollständig bewerteten Körpern
Es sei
ein vollständig bewerteter
Körper mit Bewertungsring
und Restklassenkörper
,
und es sei
ein normiertes Polynom. Aus dem henselschen
Lemma folgt: Hat die Reduktion
eine einfache Nullstelle in
,
so hat
eine Nullstelle in
.
Beispiel:
Es sei
der Körper der p-adischen
Zahlen für eine Primzahl
.
Dann ist
und
.
Das Polynom
zerfällt über
in verschiedene Linearfaktoren, also hat es auch über
genau
Nullstellen, d.h.,
enthält
-te
Einheitswurzeln.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.12. 2021