
Einheitswurzel
In der Algebra werden Zahlen, deren
-te
Potenz
die Zahl 1 ergibt,
-te
Einheitswurzeln genannt.
Definition
Es sei
ein kommutativer
Ring mit Einselement und
eine natürliche
Zahl. Ein Element
heißt eine
-te
Einheitswurzel, wenn es eine der beiden gleichwertigen Bedingungen erfüllt:
;
ist Nullstelle des Polynoms
.
Die -ten
Einheitswurzeln in
bilden eine Untergruppe
der multiplikativen Gruppe
,
die oft mit
bezeichnet wird.
Eine -te
Einheitswurzel
heißt primitiv, falls
für
gilt.
Einheitswurzeln in den komplexen Zahlen
Im Körper
der komplexen Zahlen sind
die -ten
Einheitswurzeln, wobei
die imaginäre
Einheit ist. Setzt man
,
so ist
primitiv, und diese Zahlen bekommen (in der gleichen Reihenfolge) die einfache
Gestalt
.
Ist klar, um welches
es sich handelt, lässt man den unteren Index häufig fallen.
Gruppe der Einheitswurzeln
Da
und mit
und
auch
Einheitswurzeln sind, ist die Menge
aller Einheitswurzeln eine Gruppe. Die Abbildung
ist surjektiv. Der Kern dieser Abbildung ist .
Die Gruppe der komplexen Einheitswurzeln ist daher isomorph zu der Faktorgruppe
.
Geometrischer Bezug
Die -ten
Einheitswurzeln lassen sich in der komplexen Zahlenebene
geometrisch anschaulich interpretieren: Sie sind die auf dem Einheitskreis (mit
Mittelpunkt 0 und Radius 1) liegenden Ecken eines regelmäßigen
-Ecks,
wobei eine der Ecken die Zahl
ist, denn diese ist für jedes
eine
-te
Einheitswurzel.
Realteil
und Imaginärteil
der Einheitswurzeln
sind damit die Koordinaten der Ecken des
-Ecks
auf dem Kreis, d.h. für
ist
und
.
Mehr siehe unter Radizieren komplexer Zahlen.
Summe der Einheitswurzeln
Ist
eine
-te
Einheitswurzel, so gilt
Diese Aussage folgt unmittelbar aus der geometrischen Summenformel und ist ein Spezialfall der analogen Aussage für Charaktere von Gruppen.
Beispiele
Die zweiten, dritten und vierten Einheitswurzeln
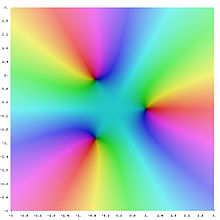
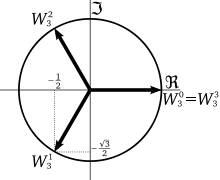
Die zweiten Einheitswurzeln sind
;
die dritten Einheitswurzeln sind
;
die vierten Einheitswurzeln sind wieder von einfacherer Form:
.
Die fünften Einheitswurzeln
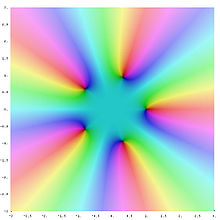
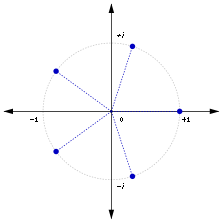
Aus
folgt
für .
Lösen dieser quadratischen
Gleichung liefert
.
Da der Winkel
im 1. Quadranten liegt, ist
positiv, und damit ist
der Realteil
von
.
Der Imaginärteil
ist nach dem Satz
des Pythagoras
.
Eigenschaften der Einheitswurzeln
Einheitswurzeln in (kommutativen) Körpern
Ist
die Charakteristik
des Körpers
,
dann ist
eine
-fache
Nullstelle des Polynoms
.
Ist
nicht Teiler der Ordnung
,
dann gelten die folgenden Aussagen auch für Körper mit Primzahlcharakteristik
.
Für zusätzliche Eigenschaften der Einheitswurzeln in solchen Körpern siehe Endlicher
Körper#Multiplikative Gruppe und diskreter Logarithmus.
- Ist
ein (kommutativer) Körper und
, dann bilden die Elemente
mit
eine zyklische Untergruppe
der multiplikativen Gruppe
.
- Die Gruppenordnung
von
ist stets ein Teiler von
.
- Ist sie gleich
, so sagt man,
„enthält die
-ten Einheitswurzeln“ und nennt
„die Gruppe der
-ten Einheitswurzeln“.
- Eine
-te Einheitswurzel ist genau dann primitiv, wenn sie die Gruppe der
-ten Einheitswurzeln erzeugt. Die Ordnung einer primitiven
-ten Einheitswurzel
ist
. Die primitiven
-ten Einheitswurzeln sind genau die Nullstellen des
-ten Kreisteilungspolynoms.
- Ist
eine primitive
-te Einheitswurzel, dann ist
eine primitive
-te Einheitswurzel (größter gemeinsamer Teiler).
- Die Anzahl der primitiven
-ten Einheitswurzeln ist
(Eulersche Phi-Funktion).
- Erweiterungen von
, die durch Adjunktion von Einheitswurzeln entstehen, heißen Kreisteilungskörper.
- Eine endliche
multiplikative Untergruppe
eines (kommutativen) Körpers
ist zyklisch.
Beweis der letzten Aussage:
ist eine abelsche
Torsionsgruppe. Sie ist also zu einem direkten Produkt
mit
isomorph ( :=
Menge der positiven Primzahlen). Und die
sind zyklisch, weil die Gruppenelemente der Ordnung
allesamt Nullstellen von
sind und damit Potenzen voneinander. Schließlich ist wegen der Teilerfremdheit
von Potenzen verschiedener Primzahlen das direkte Produkt zyklisch.
Beispiel für Einheitswurzeln in nicht-kommutativen (Schief)körpern
Im nicht-kommutativen
Schiefkörper der Quaternionen
hat das Polynom
die unendlich vielen Nullstellen
mit
.
Die Quaternionengruppe
ist eine endliche nicht-kommutative Untergruppe der multiplikativen Gruppe
.
Sie hat die Ordnung 8 und den Exponenten
4. Für weitere endliche Untergruppen von
siehe Quaternion#Die
endlichen Untergruppen.
Einheitswurzeln in Restklassenringen
- Im Ring
der ganzen Zahlen modulo
ist die Zahl
eine primitive
-te Einheitswurzel, denn in diesem Ring gilt
.
- Im Ring
der ganzen Zahlen modulo
ist die Zahl
eine primitive
-te Einheitswurzel.
Diese beiden speziellen Restklassenringe sind für die Computeralgebra höchst
bedeutsam, denn sie ermöglichen eine nochmals drastisch beschleunigte Variante
der schnellen
diskreten Fouriertransformation. Dies liegt darin begründet, dass Addition
und Multiplikation dieser Restklassenringe durch entsprechende zyklische
Addition und Multiplikation in einem unwesentlich größeren Restklassenring
ersetzt werden können, und damit in binärer Zahlendarstellung die Multiplikation
mit Potenzen der Zahl
eine zyklische binäre Shift-Operation bedeutet, was wesentlich schneller
durchführbar ist als eine allgemeine Multiplikation zweier Zahlen. Die
erhebliche Zeitersparnis für die diskrete Fourier-Transformation ergibt sich aus
der Tatsache, dass während der schnellen Fouriertransformation viele
Multiplikationen mit der gewählten Einheitswurzel durchzuführen sind.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.02. 2021