
Zwischenwertsatz
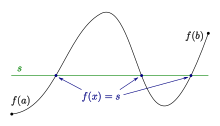
In der reellen Analysis ist der Zwischenwertsatz ein wichtiger Satz über den Wertebereich von stetigen Funktionen.
Der Zwischenwertsatz sagt aus, dass eine reelle Funktion ,
die auf einem abgeschlossenen
Intervall
stetig ist, jeden Wert zwischen
und
annimmt. Haben insbesondere
und
verschiedene Vorzeichen,
so garantiert der Zwischenwertsatz die Existenz von mindestens einer Nullstelle von
im offenen Intervall
.
Dieser Sonderfall ist als Nullstellensatz von Bolzano bekannt und nach Bernard Bolzano
benannt. Andererseits kann der Zwischenwertsatz aber auch aus dem
Nullstellensatz hergeleitet werden. Die beiden Formulierungen sind also
äquivalent.
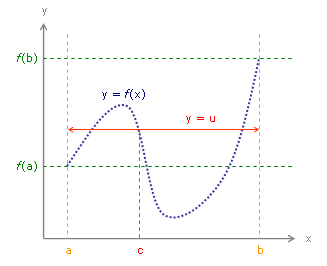
Satz
Es sei
eine stetige
reelle Funktion, die auf einem abgeschlossenen
Intervall definiert ist. Dann nimmt
jeden beliebigen Wert
zwischen
und
an mindestens einer Stelle
an (d.h.
).
Formal heißt das, es existiert zu jedem
(falls
)
bzw.
(falls
)
ein
mit
.
Anders formuliert bedeutet dies mit
und
,
dass
.
Beweis
Der Beweis setzt voraus, dass die Grenzen des betrachteten abgeschlossenen
Intervalls
endlich sind (gleichbedeutend:
ist auch beschränkt und somit kompakt.).
Tatsächlich gilt der Zwischenwertsatz auch für unbeschränkte
abgeschlossene Intervalle; die dann zu beweisenden Behauptungen finden sich im
Abschnitt Verallgemeinerung
dieses Artikels.
Ohne
Beschränkung der Allgemeinheit gelte ,
und es sei
.
- Die Funktion
ist (als Komposition
zweier stetiger Funktionen) stetig auf .
Wegen
ist
,
wegen
ist
,
insgesamt also
Zum Beweis der Behauptung ist hinreichend zu zeigen, dass
eine Nullstelle
hat, denn
.
Zum Nachweis der Existenz von
dient eine Folge
von Intervallen
mit folgenden (zu beweisenden) Eigenschaften:
- Sämtliche Glieder
respektieren die Ungleichungskette (1) (und schließen daher
ein).
ist eine Intervallschachtelung (und definiert genau ein
).
ist eine Nullstelle von
.
Eine Intervallfolge
sei rekursiv
definiert mit
für das erste Intervall.
ist der Mittelpunkt des
-ten Intervalls.
Die Grenzen des jeweils folgenden Intervalls
seien
- für
:
und
- für
:
.
zu (i): Mit (1) ist
nicht positiv,
nicht negativ.
- Beim Übergang von
zu
wird genau eine der Intervallgrenzen
(bzw.
) genau dann durch eine neue Grenze
ersetzt, wenn auch
nicht positiv (bzw. nicht negativ) ist.
- Also[Anm
1] gilt
für
bzw.
, q.e.d.
zu (ii): Im
folgenden Intervall
ist die ersetzende Grenze
größer als eine ersetzte untere Grenze
,
aber kleiner als eine ersetzte obere Grenze
,
indem
der Intervallmittelpunkt von
ist. Da der Übergang von
zu
den Intervalldurchmesser
halbiert, ist der Intervalldurchmesser fast
aller Folgeglieder kleiner als ein beliebig vorgegebener. (
ist eine Nullfolge.)
Behauptung:
ist monoton
steigend
.
- Beweis: Für
ist nichts zu beweisen. Für
folgt aus
:
.
Behauptung:
ist monoton fallend
.
- Beweis: Für
ist nichts zu beweisen. Für
folgt aus
:
.
Behauptung: ,
ist eine Nullfolge.
- Beweis: Der Durchmesser des Intervalls
ist
- für
:
;
- für
:
.
- Insgesamt können alle
auch
geschrieben werden, und
ist wegen
eine (geometrische) Nullfolge.[Anm 2]
Mit (2), (3) und (4) ist
eine Intervallschachtelung, die genau eine Zahl
definiert.
Mit
liegt
im Intervall der Voraussetzung, q.e.d.
Bemerkung: Endlich viele Intervalle einer wie
konstruierten Intervallschachtelung liegen dem numerischen Verfahren Bisektion zugrunde.
zu (iii):
ist gemeinsamer Grenzwert
der Folgen
und
;
wegen Stetigkeit von
ist
gemeinsamer Grenzwert der Folgen
und
.
Die Beschränktheit
der Folgen
und
bewirkt, dass
weder positiv noch negativ ist.
Aus (ii) folgt[Anm 3]
,
hieraus mit dem Folgenkriterium
vermöge der Stetigkeit von
bei
:
.
Mit (i) haben die Folgen
bzw.
eine obere bzw. unterer Schranke, die sich auf den jeweiligen Grenzwert
fortsetzt:[Anm
4]
,
ebenso
,
insgesamt also
,
q.e.d.
Alternativer Beweis
Es reicht, den Fall
zu betrachten. Sei
beliebig. Für
und
ist die Behauptung klar. Im Folgenden sei
also o.B.d.A. aus dem offenen Intervall
.
Es ist zu zeigen, dass ein
existiert mit
.
Setze
.
Es gilt ,
da
.
Da
beschränkt ist, ist
eine reelle Zahl.
Behauptung: Es gibt eine Folge
in
mit
.
Hierzu: Da
die größte untere Schranke ist, ist
keine untere Schranke. Mithin gibt es zu jedem
ein
mit
.
Außerdem ist natürlich
,
da
eine untere Schranke ist. Die so konstruierte Folge
konvergiert nach dem Intervallschachtelungsprinzip wie gewünscht gegen
.
Dies zeigt die Behauptung.
Aus
folgt mit den Grenzwertsätzen auch
.
Da
stetig ist, gilt
.
Wegen
ist weiter
.
Insbesondere folgt
,
da
.
Wegen
ist
für alle großen
.
Weil
folgt
und somit
.
Zusammen mit der Stetigkeit von
in
ergibt sich durch Grenzübergang
.
Insgesamt also
.
q.e.d.
Beispiel
Die Kosinus-Funktion
ist im Intervall
stetig, es ist
und
.
Der Zwischenwertsatz besagt dann, dass der Kosinus mindestens eine Nullstelle im
Intervall
hat. Tatsächlich gibt es in dem Intervall genau eine Nullstelle bei
.
Verallgemeinerung
Der Zwischenwertsatz ist ein Spezialfall des folgenden Satzes aus der Topologie: Das Bild einer zusammenhängenden Teilmenge eines topologischen Raumes bezüglich einer stetigen Abbildung ist wieder zusammenhängend.
Daraus ist wieder der Zwischenwertsatz zu erhalten, weil Stetigkeit einer Funktion im topologischen Sinne die im Zwischenwertsatz für reelle Funktionen geforderte einschließt, und weil eine Teilmenge der reellen Zahlen genau dann zusammenhängend ist, wenn sie ein Intervall ist. Anders als hier im Abschnitt "Beweis" braucht das betrachtete Intervall bei diesem Aufbau nicht beschränkt zu sein.
Zwischenwertsatz für Ableitungen (Satz von Darboux)
Eine zum obigen Zwischenwertsatz analoge Aussage gilt für Ableitungsfunktionen:
Ist
eine auf dem Intervall
definierte differenzierbare
Funktion mit
,
so nimmt die Ableitungsfunktion
jeden Wert zwischen
und
an.
Man beachte, dass dies auch gilt, wenn die Ableitungsfunktion nicht stetig ist. Der Satz folgt aus dem Mittelwertsatz der Differentialrechnung.
Literatur
- >G. M. Fichtenholz: Differential- und Integralrechnung I. 8. Auflage. Deutscher Verlag der Wissenschaften, Berlin 1973.
- Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 8. Aufl. 2006, ISBN 3-528-67224-2
Anmerkungen
- ↑ Der Gedankengang entspricht einer vollständigen Induktion.
- ↑ Weiteres zur Konvergenz geometrischer Folgen hier.
- ↑ wegen der Konvergenz der Grenzfolgen einer Intervallschachtelung
- ↑ vgl. Aussage zum Grenzwert einer beschränkten konvergenten Folge


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.12. 2021