
Mittelwertsatz der Differentialrechnung
Der Mittelwertsatz ist ein zentraler Satz der Differentialrechnung, eines Teilgebiets der Analysis (Mathematik).
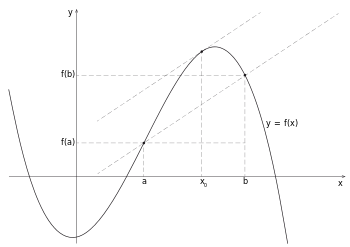
Veranschaulicht lässt sich der Mittelwertsatz geometrisch so deuten, dass es unter den unten genannten Voraussetzungen zwischen zwei Punkten eines Funktionsgraphen mindestens einen Kurvenpunkt gibt, für den die Tangente parallel zurSekante durch die beiden gegebenen Punkte ist.
Die Aussage des Satzes lässt sich sowohl auf den Quotienten zweier Funktionen übertragen als auch auf Funktionen mehrerer Variablen anwenden.
Aussage des Mittelwertsatzes
Es sei
eine Funktion,
die auf dem abgeschlossenen Intervall
(mit
)
definiert und stetig
ist. Außerdem sei die Funktion
im offenen Intervall
differenzierbar.
Unter diesen Voraussetzungen gibt es mindestens ein
,
so dass
gilt.
Geometrisch gedeutet bedeutet dies, dass die Sekantensteigung an mindestens einer Zwischenstelle als Steigung der Tangente an den Graphen der Funktion auftritt.
Beweis im eindimensionalen Fall
Es sei eine Hilfsfunktion
definiert, mit
ist stetig in
und in
differenzierbar. Es gilt
.
Nach dem Satz von Rolle existiert daher ein
mit
.
Da
folgt die Behauptung.
Beispiel einer Anwendung des Mittelwertsatzes
Als typische Anwendung des Mittelwertsatzes kann gezeigt werden, dass
für alle
gilt: Ohne Einschränkung können wir
annehmen. Da die Sinusfunktion im Intervall
differenzierbar ist, existiert nach dem Mittelwertsatz ein
,
so dass
gilt. Wegen
für alle
,
erhält man
Allgemein kann so nachgewiesen werden, dass stetig differenzierbare Funktionen lokal Lipschitz-stetig sind.
Erweiterter Mittelwertsatz der Differentialrechnung
Der Mittelwertsatz lässt sich in folgender Weise verallgemeinern:
Es seien
und
zwei Funktionen, die auf dem abgeschlossenen Intervall
(mit
)
definiert und stetig und auf dem offenen Intervall
differenzierbar sind. Unter diesen Voraussetzungen existiert mindestens ein
,
so dass
gilt.
Wird zusätzlich
auf dem Intervall
vorausgesetzt, so ist insbesondere
sowie
und man kann den erweiterten Mittelwertsatz in der üblichen Bruchform
schreiben,
-
.
Beweis
Ist ,
so muss für den verallgemeinerten Mittelwertsatz der Differentialrechnung
gezeigt werden, dass für ein
Folgendes gilt
.
Nach dem Satz
von Rolle gibt es ein ,
für das
gilt.
Ist ,
so kann man die Funktion
auf dem Intervall
definieren. Da
gilt, gibt es nach dem Satz von Rolle ein
mit
,
also
.
Durch Umstellen dieser Gleichung folgt die Behauptung.
Mittelwertsatz für reellwertige Funktionen mehrerer Variablen
In der mehrdimensionalen Analysis lautet der Mittelwertsatz wie folgt:
Es sei
eine Abbildung mit
,
weiter sei
differenzierbar auf einer offenen Menge
.
Außerdem seien
mit
und ihre Verbindungsstrecke
.
Dann existiert mindestens ein
mit
und
und es gilt:
Für
entspricht der Satz dem oben erwähnten Mittelwertsatz der eindimensionalen
Differentialrechnung.
bezeichnet hierbei den Gradienten
an der Stelle
,
der in einem Skalarprodukt
auftritt.
Geometrisch gedeutet, tritt die Sekantensteigung zwischen
und
an mindestens einer Stelle aus
als Steigung in Richtung des Vektors
auf.
Beweis im mehrdimensionalen Fall
Betrachtet man die Funktion
mit
,
so ist
stetig auf
und differenzierbar auf
.
Somit folgt aus dem Mittelwertsatz der eindimensionalen Analysis, dass ein
derart existiert, dass
.
Aus der Kettenregel folgt nun:
.
Dies lässt sich folgendermaßen zusammenfassen:
Substituiert man nun
durch
,
so ergibt sich
,
womit die Aussage des Satzes bewiesen wäre.
Mittelwertsatz für vektorwertige Funktionen mehrerer Variablen
Eine Ausdehnung des Satzes auf Funktionen
ist nur unter veränderten geometrischen Voraussetzungen bzw. Verschärfungen
möglich. Insbesondere wird der Pool der in Frage kommenden linearen Abbildungen
erheblich über die Ableitungen auf der Strecke
hinaus erweitert:
Falls die Ableitungen von
auf der gesamten Strecke
beschränkt sind (es handelt sich um Jacobimatrizen, also
beschränkt bezüglich einer Norm
auf
,
zum Beispiel der Operatornorm),
so gibt es eine lineare Abbildung
aus der abgeschlossenen konvexen
Hülle der Ableitungen auf der Verbindungsstrecke, sodass
gilt.
Der Beweis hierfür erfolgt über den Hauptsatz der Differential- und
Integralrechnung auf die Hilfsfunktionen
. Warum die Ableitungen auf der Strecke
nicht ausreichen, kann man folgendermaßen verstehen: Auf die einzelnen
Komponenten
der vektorwertigen
Funktion
kann einerseits der Mittelwertsatz für reellwertige Funktionen mehrerer
Veränderlicher angewandt werden. Andererseits ist keinesfalls gewährleistet,
dass die zugehörige Stelle auf
,
an der die passende Ableitung gefunden wird, für alle Komponentenfunktionen
dieselbe ist. Man muss sich daher in einer größeren Menge umschauen, eben der
konvexen Hülle der Ableitungen auf der Strecke.
Anschauliche Bedeutung
Beschreibt die Funktion beispielsweise eine Strecke in Abhängigkeit von einer Zeit, dann ist die Ableitung die Geschwindigkeit. Der Mittelwertsatz besagt dann: Auf dem Weg von A nach B muss man mindestens zu einem Zeitpunkt so schnell gewesen sein wie seine Durchschnittsgeschwindigkeit.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.02. 2019