Mittelwertsatz der Integralrechnung
Der Mittelwertsatz der Integralrechnung (auch Cauchyscher Mittelwertsatz genannt) ist ein wichtiger Satz der Analysis. Er erlaubt es, Integrale abzuschätzen, ohne den tatsächlichen Wert auszurechnen und liefert einen einfachen Beweis des Fundamentalsatzes der Analysis.
Aussage
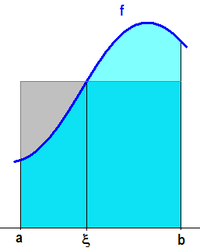
Hier wird das Riemann-Integral betrachtet. Die Aussage lautet:
Sei
eine stetige
Funktion, sowie
integrierbar und entweder
oder
(d.h. ohne Vorzeichenwechsel).
Dann existiert ein
,
so dass
gilt. Manche Autoren bezeichnen die obige Aussage als erweiterten
Mittelwertsatz und die Aussage für
als Mittelwertsatz oder ersten Mittelwertsatz. Für
bekommt man den wichtigen Spezialfall:
,
der sich geometrisch leicht deuten lässt: Die Fläche unter der Kurve zwischen
und
ist gleich dem Inhalt eines Rechtecks mittlerer Höhe.
Beweis
Sei
auf dem Intervall
.
Der andere Fall kann durch Übergang zu
auf diesen zurückgeführt werden. Sind
und
das Infimum
bzw. das Supremum
von
auf
,
so folgt aus
daher
.
Mit der Monotonie
und Linearität des
Riemann-Integrals ergibt sich:
Bezeichne
Ist
,
folgt die Aussage sofort. Für positives
gilt
Bezeichnen wir diesen Wert mit ,
so folgt aus dem Zwischenwertsatz,
dass es ein
mit
welcher das Gewünschte leistet. Man kann sogar zeigen, dass
im Innern des Intervalls
gefunden werden kann.
Bedingung an g
Die Bedingung, dass
oder
gilt, ist wichtig. In der Tat gilt der Mittelwertsatz für Funktionen
,
die diese Bedingung nicht erfüllen, nicht im Allgemeinen, denn für
und
ist
,
jedoch
für alle
.
Zweiter Mittelwertsatz der Integralrechnung
Seien
Funktionen,
>
monoton und
stetig. Dann existiert ein
,
so dass
Im Fall, dass
sogar stetig differenzierbar ist, kann man
wählen. Der Beweis erfordert partielle
Integration, den Fundamentalsatz der Analysis und den obigen Satz.
Siehe auch
- Integralrechnung #Mittelwerte stetiger Funktionen
- Mittelwert #Mittelwert einer Funktion
- Mittelwertsatz der Differentialrechnung


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.03. 2020