
Funktionsgraph

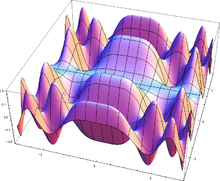
Als Funktionsgraph oder kurz Graph (seltener:
Funktionsgraf oder Graf) einer Funktion
bezeichnet man in der Mathematik
die Menge aller geordneten
Paare
aus den Elementen
der Definitionsmenge
und den zugehörigen Funktionswerten
.
Mitunter können diese Paare als Punkte in der Zeichenebene oder im Anschauungsraum interpretiert werden, sie werden auch Kurve, Kurvenverlauf oder ebenfalls Funktionsgraph genannt.
Definition
Der Graph einer Funktion
mit Definitionsmenge
und Zielmenge
ist die Menge
.
Der Graph ist somit eine spezielle Teilmenge des kartesischen Produkts aus Definitions- und Zielmenge. Er besteht aus allen Paaren, bei denen die erste Komponente ein Element der Definitionsmenge und die zweite Komponente das diesem Element durch die Funktion zugeordnete Element der Zielmenge ist.
Spezialfälle und Beispiele
Der Graph einer Funktion
mit
ist eine Teilmenge von
und kann somit als Punktmenge bzw. geometrische
Figur in der Ebene
aufgefasst werden. Beispiele sind:
- Der Graph einer linearen
Funktion
ist eine Gerade.
- Der Graph einer quadratischen
Funktion
mit
ist eine Parabel.
- Der Graph der Kehrwertfunktion
ist eine Hyperbel.
Die Graphen von Funktionen
oder
sind Teilmengen von
und können als räumliche Figuren ebenfalls noch bildlich dargestellt werden.
Beispiele sind:
- Der Graph einer stetigen
Funktion
ist eine Fläche im dreidimensionalen Raum. Zum Beispiel ist der Graph der Funktion
ein elliptisches Paraboloid.
- Der Graph einer stetigen Funktion
ist eine Kurve im dreidimensionalen Raum. Zum Beispiel ist der Graph der Funktion
eine Schraubenlinie.
Verwendung in der Mathematik
In mengentheoretischen
Definitionen von Funktionen werden diese oftmals gerade als Menge der
Stelle-Wert-Paare definiert, das heißt, der Graph wäre nichts anderes als die
Funktion selbst, also .
Auf diese Kuriosität wies bereits 1960 Jean
Dieudonné hin:
-
- It is customary, in the language, to talk of a mapping and a functional graph as if they were two kinds of objects in one-to-one correspondence, and to speak therefore of “the graph of a mapping”, but this is a mere psychological distinction (corresponding to whether one looks on F either “geometrically” or “analytically”).
Bei mathematischen Betrachtungen, die nicht direkt im Kontext der
mengentheoretischen Fundierung der mathematischen Begriffe stehen, setzt man
jedoch in der Regel keine Mengenstruktur einer Funktion voraus, sondern fordert
lediglich die Definiertheit des Bildes zu einer gegebenen Stelle.
Mengenoperationen werden dann nicht auf Funktionen ausgeführt (etwa würde
dann meist nicht als sinnvoller Ausdruck angesehen), in einigen Fällen ist es
jedoch gerade praktisch eine Funktion als Menge zu betrachten mit den auf Mengen
definierten Operationen und Eigenschaften; diese Betrachtung geschieht über den
Graphen der Funktion. Neben der Möglichkeit, eine Funktion dadurch als
geometrische Figur zu betrachten, seien hier als weitere Beispiele genannt:
- In jedem polnischen Raum ist eine Funktion genau dann Borel-messbar, wenn der Graph eine Borel-Menge ist.
- Satz vom abgeschlossenen Graphen: Ein linearer Operator zwischen Banachräumen ist genau dann stetig, wenn sein Graph abgeschlossen ist.
Graphen im Sinne der graphischen Darstellung
Die graphische Darstellung ist kein mathematisches Objekt. Sie dient im Rahmen der Mathematik der Veranschauung und lässt Mutmaßungen über die Eigenschaften einer Funktion zu.
Graphen unstetiger Funktionen, Definitionslücken
In der Darstellung der Graphen von unstetigen
Funktionen oder von Funktionen mit Definitionslücken
wird häufig durch
angedeutet, dass ein Punkt zum Graphen gehört, und durch
,
dass ein Punkt nicht Teil des Graphen ist. Ein Beispiel ist die Illustration der
Vorzeichenfunktion
(auch „Signumfunktion“).
Beispiele
Drei Beispiele für Funktionsgraphen:
| Funktion | Graph | Anmerkung |
|---|---|---|
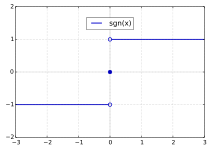 |
Der Funktionswert der Vorzeichenfunktion an der Stelle 0 ist 0. | |
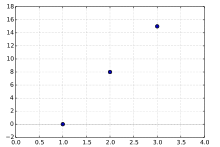 |
Da der Definitionsbereich die Menge | |
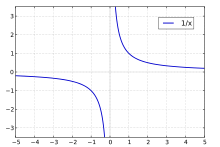 |
Für |
Literatur
- Hermann Schichl, Roland Steinbauer: Einführung in das mathematische Arbeiten. Berlin/Heidelberg: Springer 2012, 2. Auflage, ISBN 978-3-642-28645-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.09. 2022