Parabel (Mathematik)

Die Parabel ist einer der Kegelschnitte.

Ein hüpfender Ball beschreibt – wenn man Reibungsverluste vernachlässigt – Parabelbögen.

Wasserstrahlen beschreiben ebenfalls Parabeln, wenn man die Reibung vernachlässigt.

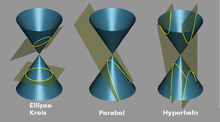
In der Mathematik ist eine Parabel (von lateinisch parabola zu altgriechisch παραβολή parabolḗ, deutsch ‚Nebeneinanderstellung, Vergleichung, Gleichnis, Gleichheit‘; zurückzuführen auf παρά pará, deutsch ‚neben‘ und βάλλειν bállein, deutsch ‚werfen‘) eine Kurve zweiter Ordnung und ist daher über eine algebraische Gleichung zweiten Grades beschreibbar. Neben dem Kreis, der Ellipse und der Hyperbel zählt sie zu den Kegelschnitten: Sie entsteht beim Schnitt eines geraden Kreiskegels mit einer Ebene, die parallel zu einer Mantellinie verläuft und nicht durch die Kegelspitze geht. Aufgrund dieser sehr speziellen Schnittvorausetzung spielt die Parabel unter den Kegelschnitten eine besondere Rolle: Sie besitzt nur einen Brennpunkt und alle Parabeln sind zueinander ähnlich.

Die Parabel wurde von Menaichmos entdeckt und von Apollonios von Perge (etwa 262–190 v. Chr.) als parabolḗ benannt.

Parabeln treten in der Mathematik häufig als Graphen quadratischer Funktionen $x\mapsto f(x)=ax^{2}+bx+c$ auf.

Auch im täglichen Leben spielen Parabeln eine Rolle:

Die Funktionsweise von Parabolantennen und Parabolspiegeln beruht auf der geometrischen Eigenschaft der Parabel, parallel zu ihrer Achse einfallende Strahlen im Brennpunkt zu sammeln (siehe weiter unten).
Ein schräg nach oben geworfener Stein bewegt sich näherungsweise auf einer parabelförmigen Bahn, der Wurfparabel (s. hüpfender Ball, Springbrunnen). Dies hängt damit zusammen, dass Wurfbewegungen durch quadratische Funktionen beschrieben werden.
In einem Flugzeug, das sich entlang einer Wurfparabel bewegt, herrscht Schwerelosigkeit. Solche Parabelflüge werden zum Training von Astronauten verwendet.
In der Mathematik werden Parabeln häufig zur Approximation komplizierterer Funktionen verwendet, da sie nach den Geraden (Gleichung: ) die einfachsten gekrümmten Funktionsgraphen (Gleichung: ) sind und sich besser als Geraden an gekrümmte Funktionsgraphen anschmiegen können. Im CAD-Bereich (Computer Aided Design) treten Parabeln als Bézierkurven auf. Ein Vorteil der Parabeln gegenüber Kreisen, Ellipsen und Hyperbeln besteht darin, dass man sie als Funktionsgraph von Polynomfunktionen 2. Grades beschreiben kann.

Definition mit Leitlinie

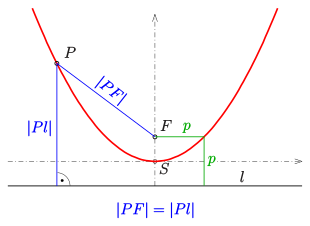
Parabel: Definition mit Brennpunkt F, Leitlinie l (schwarz) und Halbparameter p (grün). Das Lot Pl und die Strecke PF (jeweils blau) sind für alle Punkte P der Parabel (rot) gleich lang

Eine Parabel kann geometrisch als Ortslinie beschrieben werden:

Eine Parabel ist der geometrische Ort aller Punkte , deren Abstand d(P,F)

zu einem speziellen festen Punkt – dem Brennpunkt – gleich dem Abstand d(P,l)

zu einer speziellen Geraden – der Leitlinie

– ist.

Als Punktmenge notiert:

$\{P \mid d(P,F) = d(P,l)\}$

Der Punkt, der in der Mitte zwischen Brennpunkt und Leitgerade liegt, heißt Scheitel oder Scheitelpunkt der Parabel. Die Verbindungsgerade von Brennpunkt und Scheitel wird auch Achse der Parabel genannt. Sie ist die einzige Symmetrieachse der Parabel.

Führt man Koordinaten so ein, dass $F=(0,f)\ ,f>0$ ist und die Leitlinie die Gleichung y=-f besitzt, so ergibt sich für P=(x,y) aus $d(P,F)=d(P,l)$ die Gleichung

$y=\tfrac{1}{4f}x^2$

einer nach oben geöffneten Parabel.

Die halbe Weite der Parabel in der Höhe des Brennpunktes ergibt sich aus $y=f={\tfrac {1}{4f}}x^{2}$ zu p=2f und heißt (analog zu Ellipse und Hyperbel) der Halbparameter der Parabel. Der Halbparameter ist wie bei Ellipse (im Hauptscheitel) und Hyperbel der Scheitelkrümmungskreisradius, also der Radius des Krümmungskreises an den Scheitelpunkt. Bei einer Parabel ist außerdem der Abstand des Brennpunktes zur Leitlinie. Die Gleichung der Parabel lässt sich damit auch in der folgenden Form schreiben:

Vertauscht man und , so erhält man mit

die Gleichung einer nach rechts geöffneten Parabel.

Aufgrund der Definition ist eine Parabel die Äquidistanz-Kurve zu ihrem Brennpunkt und ihrer Leitlinie.

Parabel als Funktions-Graph

Parabeln

(Parabelschar)

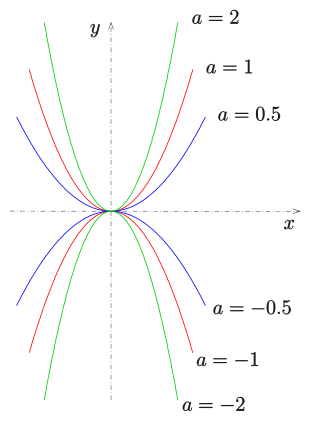
Eine nach oben oder unten geöffnete Parabel mit Scheitel im Nullpunkt (0,0) und der -Achse als Achse wird (in kartesischen Koordinaten) durch eine Gleichung

$y=ax^{2}{\text{ mit }}a\neq 0$

beschrieben. Für a>0 sind die Parabeln nach oben geöffnet, für a<0 nach unten (siehe Bild). Dabei gilt:

Der Brennpunkt ist $(0,{\tfrac {1}{4a}})$ ,
der Halbparameter ist $p=\tfrac{1}{2a}$ ,
die Leitlinie hat die Gleichung $y=-{\tfrac {1}{4a}}$ und
die Tangente im Punkt hat die Gleichung $y=2ax_{0}x-ax_{0}^{2}$ .

Für a=1 erhält man die Normalparabel y=x^2 . Ihr Brennpunkt ist $(0,{\tfrac {1}{4}})$ , der Halbparameter $p=\tfrac{1}{2}$ und die Leitlinie hat die Gleichung $y=-{\tfrac {1}{4}}$ .

Nach einer Verschiebung $(x,y)\mapsto (x+x_{0},y+y_{0})$ erhält man die Scheitelform einer beliebigen nach oben oder unten geöffneten Parabel:

$y=a(x-x_{0})^{2}+y_{0}\ ,\ a\neq 0$ mit dem Scheitel $S=(x_{0},y_{0})$

Durch Ausmultiplizieren ergibt sich die allgemeine Gleichung einer nach unten oder oben geöffneten Parabel:

$y=ax^{2}+bx+c{\text{ mit }}a,b,c\in \mathbb{R} ,a\neq 0$

Sie ist der Graph der quadratischen Funktion

$f(x)=ax^{2}+bx+c$ .

Ist die Funktion $f(x)=ax^{2}+bx+c$ gegeben, so findet man den Scheitel durch quadratische Ergänzung:

$S=(x_{0},y_{0})=(-{\tfrac {b}{2a}},c-{\tfrac {b^{2}}{4a}})$

Jede Parabel ist zur Normalparabel y=x² ähnlich

Parabel $\color {blue}{y=2x^{2}}$ mit dem Faktor 2 am Ursprung gestreckt, das Ergebnis ist die Parabel $\color {red}{y=x^{2}}$ .

In der Geometrie sind zwei Figuren genau dann zueinander ähnlich, wenn sie durch eine Ähnlichkeitsabbildung ineinander übergeführt werden können. Eine Ähnlichkeitsabbildung ist eine Hintereinanderausführung von zentrischen Streckungen, Verschiebungen, Drehungen und Spiegelungen.

Eine beliebige Parabel $\mathcal P$ hat einen Scheitel $S=(s_{1},s_{2})$ und kann durch die Verschiebung $(x,y)\mapsto (x-s_{1},y-s_{2})$ und eine geeignete Drehung um den Ursprung so transformiert werden, dass die transformierte Parabel den Ursprung als Scheitel und die -Achse als Achse besitzt. Also ist die Parabel $\mathcal P$ zu einer Parabel mit der Gleichung y=ax^2 ähnlich. Durch die zusätzliche zentrische Streckung $(x,y)\mapsto (ax,ay)$ wird die Parabel schließlich in die Normalparabel $y=x^{2}$ übergeführt. Also gilt

Jede Parabel ist zur Normalparabel ähnlich.

Bemerkungen:

Diese Aussage ist nur für Parabeln richtig und nicht für Ellipsen/Einheitskreis und Hyperbeln/Einheitshyperbel!
Es gibt andere einfache affine Abbildungen, die die Parabel auf die Normalparabel abbilden. Zum Beispiel $(x,y)\mapsto \left(x,{\tfrac {y}{a}}\right)$ . Aber diese Abbildung ist keine Ähnlichkeitsabbildung!

Parabel als Sonderfall der Kegelschnitte

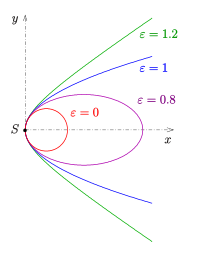
Kegelschnittschar mit Scharparameter $\varepsilon$

Die Schar der Kegelschnitte, deren Achse die -Achse ist und die einen Scheitelpunkt im Ursprung (0,0) mit dem Scheitelkrümmungskreisradius (beliebig, aber fest) haben, lässt sich durch die Gleichung

$y^{2}=2px+(\varepsilon ^{2}-1)x^{2}\qquad ,\ \varepsilon \geq 0$

beschreiben.

Für $\varepsilon=0$ erhält man einen Kreis (Scheitelkrümmungskreis aller Kegelschnitte der Schar),
für $0<\varepsilon <1$ eine Ellipse,
für $\varepsilon =1$ eine Parabel und
für $\varepsilon>1$ eine Hyperbel (s. Bild).

Die allgemeine Gleichung für Kegelschnitte lautet

$a x^2 + bx y + c y^2 + dx + e y + f = 0 \quad,$ a, b, c nicht alle 0.

Um zu erkennen, welcher Kegelschnitt durch eine konkrete Gleichung beschrieben wird, muss man eine Hauptachsentransformation (Drehung und anschließende Verschiebung des Koordinatensystems) durchführen. Siehe hierzu Kegelschnitt.

Parabel als Kegelschnitt

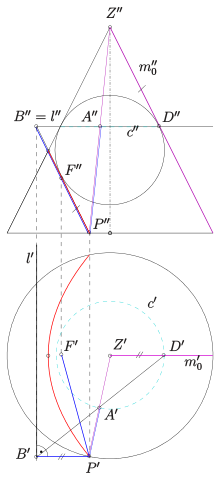
Dandelin-Kugel: Parabel-Fall (Grund- und Aufriss)

Schneidet man einen senkrechten Kreiskegel mit einer Ebene $\pi$ , deren Neigung gleich der Neigung der Mantellinien des Kegels ist, so ergibt sich eine Parabel als Schnittkurve (s. Bild, rote Kurve). Den Nachweis der definierenden Eigenschaft bzgl. Brennpunkt und Leitlinie (s. oben) führt man mit Hilfe einer Dandelin’schen Kugel, d.i. eine Kugel, die den Kegel in einem Kreis und die Parabel-Ebene in einem Punkt berührt. Es stellt sich heraus, dass der Brennpunkt der Schnittparabel und die Schnittgerade der Ebene des Berührkreises mit der Ebene $\pi$ die Leitlinie ist.

sei ein beliebiger Punkt der Schnittkurve.
Die Strecken $\overline{PF}$ und $\overline{PA}$ sind tangential zur Kugel und damit gleich lang.
Die Ebenen durch die Mantellinie $m_{0}$ schneiden die Parabelebene in einer Schar paralleler Geraden, die senkrecht zur Geraden sind ( $m_0 \parallel \pi$ !).
Anwendung des Strahlensatzes auf die sich in schneidenden Geraden und die parallelen Strecken $\overline{BP}, \overline{ZD}$ liefert die Gleichheit der Länge der Strecken $\overline{PA}, \overline{PB}$ . (Man beachte: $\overline{ZA}, \overline{ZD}$ sind gleich lang!).
Aus der Gleichheit der Länge der Strecken $\overline{PF}$ und $\overline{PA}$ folgt schließlich

Fadenkonstruktion einer Parabel

Parabel: Fadenkonstruktion

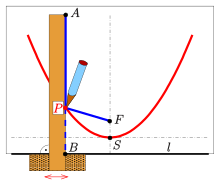
Die Definition einer Parabel mit Hilfe der Leitlinie bietet eine einfache Möglichkeit mit Hilfe eines Fadens und eines rechten Winkels (hier in T-Form zum Gleiten entlang einer Gerade) einen Parabelbogen zu zeichnen:

(0) Wahl des Brennpunktes und der Leitlinie der zu zeichnenden Parabel
(1) Faden der Länge |AB| (in der Zeichnung blau)
(2) Befestigung des einen Fadenendes im Punkt des Lineals, das andere Ende im Brennpunkt
(3) Anlegen des Winkels so, dass der eine Schenkel entlang der Leitlinie gleiten kann
(4) Mit einem Stift den Faden so spannen, dass er an der Linealkante anliegt
(5) Durch Verschieben des Lineals entlang der Leitlinie überstreicht der Stift einen Parabelbogen, denn es ist stets $|PF|=|PB|$ (Leitlinieneigenschaft).

Steiner-Erzeugung einer Parabel und der zu ihr dualen Parabel

Parabel

Parabel: Steiner-Erzeugung

Die folgende Idee, einzelne Punkte einer Parabel zu konstruieren, beruht auf der Steiner-Erzeugung eines Kegelschnitts (nach dem Schweizer Mathematiker Jakob Steiner):

Hat man für zwei Geradenbüschel in zwei Punkten $U,\, V$ (alle Geraden durch den Punkt bzw. ) eine projektive, aber nicht perspektive Abbildung $\pi$ des einen Büschels auf das andere, so bilden die Schnittpunkte zugeordneter Geraden einen nicht ausgearteten Kegelschnitt.

Für die Erzeugung einzelner Punkte der Parabel y=ax^2 gehen wir von dem Geradenbüschel im Scheitel und dem Parallelbüschel $\Pi_y$ der Parallelen zur -Achse aus (d.i. das Geradenbüschel des Fernpunktes der -Achse). Seien nun P=(x_0,y_0) ein Punkt der Parabel und A=(0,y_0) , B=(x_0,0) . Wir unterteilen die Strecke $\overline{BP}$ in gleich lange Stücke und übertragen diese Unterteilung mittels einer Parallelprojektion in Richtung auf die Strecke $\overline{AP}$ (s. Bild). Die benutzte Parallelprojektion vermittelt die nötige projektive Abbildung des Büschels in und des Parallelbüschels $\Pi_y$ . Die Schnittpunkte der zugeordneten Geraden SB_i und der -ten Parallele zur -Achse liegen dann auf der durch die Vorgaben eindeutig bestimmten Parabel (s. Bild).

Der Beweis ergibt sich durch eine einfache Rechnung. Siehe auch: projektiver Kegelschnitt.

Bemerkung: Die linke Hälfte der Parabel erhält man durch Spiegelung an der -Achse.

Bemerkung:

Auch für Ellipsen und Hyperbeln gibt es die Steiner-Erzeugung.
Statt des Scheitels der Parabel und der Scheiteltangente kann man auch einen beliebigen Punkt und seine Tangente benutzen.

Duale Parabel

Eine duale Parabel besteht aus der Menge der Tangenten einer (gewöhnlichen) Parabel.

Die vorige Steiner-Erzeugung einer Parabel lässt sich dualisieren, d.h., die Bedeutung von Punkten und Geraden wird vertauscht:

Hat man für zwei Punktreihen zweier Geraden $u,\,v$ eine projektive, aber nicht perspektive Abbildung $\pi$ der einen Punktreihe auf die andere, so bilden die Verbindungsgeraden zugeordneter Punkte einen nicht ausgearteten dualen Kegelschnitt (s. Satz von Steiner). Die Geraden sind auch Tangenten, also Elemente des dualen Kegelschnitts.

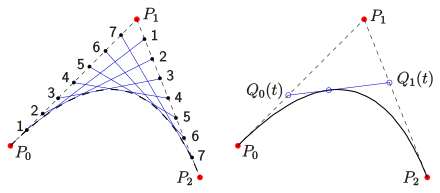
Duale Parabel und Bezierkurve vom Grad 2 (rechts: Kurvenpunkt und Teilpunkte $Q_{0},Q_{1}$ zu $t=0.4$ )

In der Praxis

gibt man drei Punkte $P_{0},P_{1},P_{2}$ vor,
unterteilt sowohl die Strecke $P_{0}P_{1}$ als auch $P_{1}P_{2}$ in jeweils gleiche Teile und nummeriert sie wie im Bild.
Die Geraden $P_{0}P_{1},P_{1}P_{2},\;(1,1),(2,2),\dotsc$ sind dann die Tangenten einer Parabel (die Elemente einer dualen Parabel).
Die Parabel ist eine Bezierkurve vom Grad 2 mit den Punkten $P_{0},P_{1},P_{2}$ als Kontrollpunkte.

Beweis:

Sind ${\vec {p}}_{0},{\vec {p}}_{1},{\vec {p}}_{2}$ die Ortsvektoren der Punkte $P_{0},P_{1},P_{2}$ , so ist

${\vec {c}}(t)=(1-t)^{2}{\vec {p}}_{0}+2t(1-t){\vec {p}}_{1}+t^{2}{\vec {p}}_{2}$

die zugehörige Bezierkurve (Parabel). Die Ableitung (der Tangentenvektor) ist

${\vec {c}}'(t)=\cdots =2\left((1-t){\vec {p}}_{1}+t{\vec {p}}_{2}-(1-t){\vec {p}}_{0}-t{\vec {p}}_{1}\right)=2\left({\vec {q}}_{1}(t)-{\vec {q}}_{0}(t)\right).$

Dabei sind $Q_{0}(t):\;{\vec {q}}_{0}(t)=(1-t){\vec {p}}_{0}+t{\vec {p}}_{1},\ Q_{1}(t):\;{\vec {q}}_{1}(t)=(1-t){\vec {p}}_{1}+t{\vec {p}}_{2}$ die zum Parameter gehörigen Teilpunkte der Strecken P_0P_1 und $P_{1}P_{2}$ . Man rechnet nach, dass ${\vec {c}}(t)=(1-t){\vec {q}}_{0}(t)+t{\vec {q}}_{1}(t)$ ist. Also ist die Gerade $Q_{0}(t)Q_{1}(t)$ Tangente im Parabelpunkt $\vec c(t)$ .

Bemerkung: Der Beweis ergibt sich auch aus den ersten zwei Schritten des de-Casteljau-Algorithmus für eine Bezierkurve vom Grad 2.

Parabel als affines Bild der Normalparabel

Parabel als affines Bild der Normalparabel

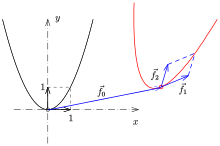
Eine andere Definition der Parabel benutzt eine spezielle geometrische Abbildung, nämlich die Affinität. Hier ist eine Parabel als affines Bild der Normalparabel definiert. Eine affine Abbildung in der reellen Ebene hat die Form ${\vec {x}}\to {\vec {f}}_{0}+A{\vec {x}}$ , wobei eine reguläre Matrix (Determinante nicht 0) und ${\vec {f}}_{0}$ ein beliebiger Vektor ist. Sind ${\vec {f}}_{1},{\vec {f}}_{2}$ die Spaltenvektoren der Matrix , so wird die Normalparabel $(t,t^2), t \in \R,$ auf die Parabel

$\vec x=\vec p(t) = \vec f_0 +\vec f_1 t +\vec f_2 t^2$

abgebildet. ${\vec {f}}_{0}$ ist ein Punkt der Parabel und $\vec f_1$ Tangentenvektor in diesem Punkt. ${\vec {f}}_{1},{\vec {f}}_{2}$ stehen i.A. nicht senkrecht aufeinander. D.h., ${\vec {f}}_{0}$ ist i.A. nicht der Scheitel der Parabel. Aber: Die Parabelachse (Symmetrieachse durch den Scheitel) ist parallel zu $\vec f_2$ . Diese Definition einer Parabel liefert eine einfache Parameterdarstellung einer beliebigen Parabel.

Da im Scheitel die Tangente zur Parabelachse senkrecht steht und die Tangentenrichtung in einem Parabelpunkt ${\vec {p}}'(t)={\vec {f}}_{1}+2t{\vec {f}}_{2}$ ist, ergibt sich der Parameter $t_{0}$ des Scheitels aus der Gleichung

${\vec {p}}'(t)\cdot {\vec {f}}_{2}={\vec {f}}_{1}\cdot {\vec {f}}_{2}+2t{\vec {f}}_{2}^{\,2}=0$ zu $t_0= -\tfrac{\vec f_1\cdot \vec f_2}{2\vec f_2^{\,2}}$ .

Die Scheitelform der Parameterdarstellung der Parabel ist

$\vec x=\vec p(t) = \vec p(t_0) +\vec p'(t_0)(t-t_0) +\vec f_2 (t-t_0)^2$ .

Beispiele:

$\vec f_0=\begin{pmatrix} 0 \\ 0 \end{pmatrix},\ \vec f_1=\begin{pmatrix} 1 \\ 0 \end{pmatrix},\ \vec f_2=\begin{pmatrix} 0 \\ a \end{pmatrix}$ liefert die übliche Parameterdarstellung der Parabel $y=ax^2: \quad (t,at^2)$ .

Parabel: Transformation auf Scheitelform (Beispiel 3)
$\vec f_0=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix},\ \vec f_1=\begin{pmatrix} \cos \varphi \\ \sin \varphi\end{pmatrix},\ \vec f_2=\begin{pmatrix} -a\sin \varphi \\ a \cos \varphi\end{pmatrix}$ liefert die Parameterdarstellung der Parabel, die aus durch Drehung um den Winkel $\varphi$ und anschließende Verschiebung um ${\vec {f}}_{0}$ hervorgeht. Die Parameterdarstellung ist schon in Scheitelform: Der Scheitel ist
$\vec f_0=\begin{pmatrix} 0 \\ 0 \end{pmatrix},\ \vec f_1=\begin{pmatrix} 1 \\ 0 \end{pmatrix},\ \vec f_2=\begin{pmatrix} 1 \\ 1 \end{pmatrix}$ liefert die Parabel ${\vec {x}}={\vec {p}}(t)={\begin{pmatrix}1\\0\end{pmatrix}}t+{\begin{pmatrix}1\\1\end{pmatrix}}t^{2}.$ Die Parameterdarstellung ist nicht in Scheitelform. Der Scheitelparameter ist $t_0=-\tfrac{1}{2\cdot2}=-\tfrac{1}{4}$ und die Scheitelform lautet:

${\vec {x}}={\vec {p}}(t)={\frac {1}{16}}{\begin{pmatrix}-3\\1\end{pmatrix}}+{\frac {1}{2}}{\begin{pmatrix}1\\-1\end{pmatrix}}(t+{\frac {1}{4}})+{\begin{pmatrix}1\\1\end{pmatrix}}(t+{\frac {1}{4}})^{2}$

Bemerkung: Sind die Vektoren ${\vec {f}}_{0},{\vec {f}}_{1},{\vec {f}}_{2}$ aus dem $\mathbb {R} ^{3}$ , so erhält man eine Parameterdarstellung einer Parabel im Raum.

Affine Selbstabbildungen der Parabel y=x²

Nicht jede affine Abbildung der reellen affinen Ebene (s. vorigen Abschnitt) bildet die Normparabel y=x^2 auf eine andere Parabel ab. Die folgenden affinen Abbildungen lassen die Parabel y=x^2 als Ganzes invariant:

$(x,y)\rightarrow (ax+b,a^{2}y+2abx+b^{2}),a\neq 0.$

Dies sind die einzigen affinen Abbildungen, die die Parabel y=x^2 invariant lassen.

Zum Beweis: Setze y=x^2 und wende die 1. binomische Formel an.

Spezialfälle:

Für $a=1,\, b=0$ bleibt jeder Punkt der Ebene fest. Diese Abbildung heißt Identität.
Für $a=1,\, b\ne 0$ wird jeder Punkt der Parabel bewegt, d.h., es gibt keinen Fixpunkt auf der Parabel.
Für ist die Abbildung involutorisch, d.h., zweimal ausgeführt ist sie die Identität. Man nennt so eine Abbildung Schrägspiegelung, da eine Gerade, nämlich $\textstyle x=\frac b 2$ , punktweise fest bleibt (siehe Abschnitt „Mittelpunkte paralleler Sehnen“). In diesem Fall gibt es genau einen Fixpunkt auf der Parabel: $(\tfrac{b}{2},\tfrac{b^2}{4})$ . Nur im Fall ist eine Schrägspiegelung eine „normale“ Spiegelung an der -Achse.

Bemerkung: Ergänzt man die reelle affine Ebene durch eine Ferngerade und deren Fernpunkte zu einer projektiven Ebene und fügt der Parabel y=x^2 den Fernpunkt der -Achse hinzu, so erhält man einen nicht ausgearteten projektiven Kegelschnitt und hat mehr Abbildungen, projektive Kollineationen, zur Verfügung. Z.B. lässt die projektive Kollineation mit

$(x,y) \rightarrow (\textstyle \frac{x}{y},\tfrac{1}{y})$

die so erweiterte Parabel invariant. Diese Abbildung ist involutorisch, lässt die Parabelpunkte (1,1),(-1,1) fix und vertauscht den Parabelpunkt (0,0) mit dem Fernpunkt der -Achse.

Eigenschaften

Brennpunkt

Parabel: Brennpunkt-Eigenschaft

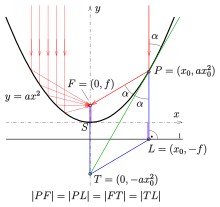
Wird ein Strahl, der parallel zur Achse einfällt, an der Parabel – d.h. an ihrer Tangente – gespiegelt, so geht der gespiegelte Strahl durch den Brennpunkt. Dieser gespiegelte Strahl wird auch Brennlinie oder Brennstrahl des betreffenden Parabelpunktes genannt. Die entsprechende Eigenschaft hat auch ein Rotationsparaboloid, also die Fläche, die entsteht, wenn man eine Parabel um ihre Achse dreht; sie wird häufig in der Technik verwendet (siehe Parabolspiegel).

Um diese Eigenschaft einer Parabel nachzuweisen, geht man von einer Parabel der Form y=ax^2 aus. Dies ist keine Einschränkung, da jede Parabel in einem geeigneten Koordinatensystem so dargestellt werden kann. Die Tangente in einem Parabelpunkt P=(x_0,ax^2_0) hat die Gleichung y=2ax_0(x-x_0)+ax^2_0 (Die Steigung der Tangente ergibt sich aus der Ableitung y'=2ax .) Die Tangente schneidet die -Achse im Punkt T=(0,-ax^2_0) . Der Brennpunkt ist $F=(0,f),\ f=\tfrac{1}{4a}$ . Der Lotfußpunkt des Lotes von auf die Leitlinie ist L=(x_0,-f) . Für eine Parabel ist |PF|=|PL| . Aus den im Bild angegebenen Koordinaten der Punkte $F,T,P,L$ erkennt man, dass |FT|=|PL| ist. Damit ist das Viereck PFTL eine Raute und die Tangente ist eine Diagonale dieser Raute und damit eine Winkelhalbierende. Hieraus folgt:

Der Brennstrahl ist die Spiegelung des einfallenden Strahls an der Tangente/Parabel.

Der Beweis und die Zeichnung zeigen eine Möglichkeit, die Tangente in einem Parabelpunkt mit Hilfe des Brennpunktes, der Leitlinie und der Raute $FPLT$ zu konstruieren. (Weitere Tangentenkonstruktionen sind im Abschnitt Tangentenkonstruktion enthalten.)

Mittelpunkte paralleler Sehnen

Parabel: Mittelpunkte paralleler Sehnen

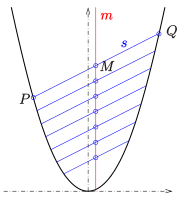
Für jede Parabel gilt:

Die Mittelpunkte paralleler Sehnen (s. Bild) liegen auf einer Gerade. Diese Gerade ist parallel zur Parabelachse.

D.h., zu jedem Punktepaar P,Q einer Sehne gibt es eine Schrägspiegelung an einer Gerade , die die Punkte P,Q vertauscht und die Parabel auf sich abbildet. Dabei versteht man unter einer Schrägspiegelung eine Verallgemeinerung einer gewöhnlichen Spiegelung an einer Gerade , bei der alle Strecken Punkt-Bildpunkt zwar parallel zueinander aber nicht unbedingt senkrecht zur Spiegelachse sind. Sind die Sehnen senkrecht zur Parabelachse, so ist die Gerade die Parabelachse und die Schrägspiegelung eine gewöhnliche Spiegelung.

Den Nachweis dieser Eigenschaft führt man am einfachsten an der Normalparabel y=x^2 durch. Da alle Parabeln affine Bilder der Normalparabel sind (s.o.) und bei einer affinen Abbildung Mittelpunkte von Strecken in die Mittelpunkte der Bildstrecken übergehen, gilt die obige Eigenschaft für alle Parabeln.

Punktkonstruktion

Eine beliebige Parabel kann in einem geeigneten Koordinatensystem durch eine Gleichung y=ax^2 beschrieben werden.

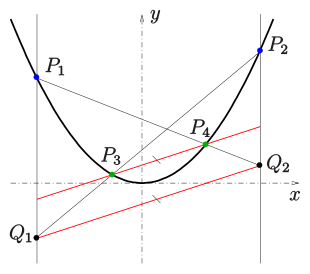
Parabel: Punktkonstruktion, $P_{1},P_{2},P_{3}\to P_{4}$

Eine weitere Möglichkeit Parabelpunkte zu konstruieren, setzt die Kenntnis von drei Parabelpunkten und der Richtung der Parabelachse voraus:

Für eine Parabel y=ax^2 gilt: Sind

$P_1=(x_1,y_1),\, P_2=(x_2,y_2),\, P_3=(x_3,y_3),\, P_4=(x_4,y_4)$ vier Punkte der Parabel und
der Schnittpunkt der Sekante $P_{1}P_{4}$ mit der Geraden sowie
der Schnittpunkt der Sekante mit der Geraden (s. Bild),

dann ist die Sekante $P_{3}P_{4}$ parallel zur Geraden Q_1Q_2 . x=x_1 und x=x_2 sind Parallelen zur Parabelachse.

Sind die drei Punkte $P_1,\, P_2,\, P_3$ einer Parabel gegeben, so kann durch Vorgabe einer Geraden durch $P_{3}$ (nicht parallel zur Parabelachse und keine Tangente) mit dieser Eigenschaft der Parabelpunkt $P_{4}$ auf dieser Geraden konstruiert werden.

Zum Beweis: Da nur Schneiden, Verbinden und Parallelität eine Rolle spielen, kann man den Beweis an der affin äquivalenten Normalparabel y=x^2 führen. Eine kurze Rechnung zeigt, dass die Gerade Q_1Q_2 parallel zur Geraden $P_{3}P_{4}$ ist.

Bemerkung: Diese Eigenschaft einer Parabel ist eine affine Version der 5-Punkte-Ausartung des Satzes von Pascal.

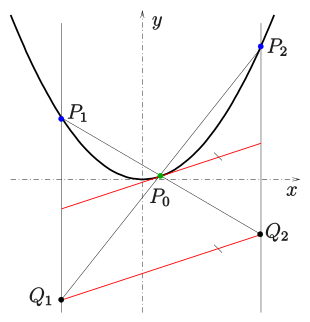
Tangentenkonstruktion

Parabel: Tangentenkonstruktion, $P_{0},P_{1},P_{2}\to$ Tangente in $P_{0}$

Parabel: Tangentenkonstruktion: $P_{1},P_{2}$ ,Tang. in $P_{1}\to$ Tang. in $P_{2}$

Eine beliebige Parabel kann in einem geeigneten Koordinatensystem durch eine Gleichung y=ax^2 beschrieben werden.

1. Methode

Für eine Parabel y=ax^2 gilt:

Sind drei Punkte der Parabel und

der Schnittpunkt der Sekante P_0P_1

mit der Gerade x=x_2

, sowie

der Schnittpunkt der Sekante P_0P_2

mit der Gerade x=x_1

(s. Bild),

dann ist die Tangente im Punkt $P_{0}$ parallel zur Gerade Q_1Q_2

(

und

sind Parallelen zur Parabelachse.)

Diese Eigenschaft kann zur Konstruktion der Tangente im Punkt $P_{0}$ benutzt werden.

Zum Beweis: Da nur Schneiden, Verbinden und Parallelität eine Rolle spielt, kann man den Beweis an der affin äquivalenten Normalparabel y=x^2 führen. Eine kurze Rechnung zeigt, dass die Gerade Q_1Q_2 die Steigung 2x_0 hat. Dies ist die Steigung der Tangente im Punkt $P_{0}$ .

Bemerkung: Diese Eigenschaft einer Parabel ist eine affine Version der 4-Punkte-Ausartung des Satzes von Pascal.

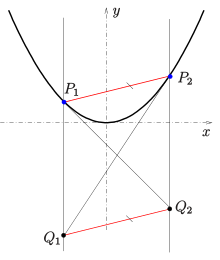
2. Methode

Eine zweite Möglichkeit, die Tangente in einem Punkt zu konstruieren, beruht auf der folgenden Eigenschaft einer Parabel y=ax^2 :

Sind zwei Punkte der Parabel und

der Schnittpunkt der Tangente in $P_{1}$ mit der Gerade x=x_2

, sowie

der Schnittpunkt der Tangente in $P_{2}$ mit der Gerade x=x_1

(s. Bild),

dann ist die Sekante $P_{1}P_{2}$ parallel zur Gerade Q_1Q_2

(

und

sind Parallelen zur Parabelachse.)

Zum Beweis: Da nur Schneiden, Verbinden und Parallelität eine Rolle spielen, kann man den Beweis an der affin äquivalenten Normalparabel y=x^2 führen.

Bemerkung: Diese Eigenschaft einer Parabel ist eine affine Version der 3-Punkte-Ausartung des Satzes von Pascal.

Achsenrichtung-Konstruktion

Parabel: Achsenrichtung-Konstruktion

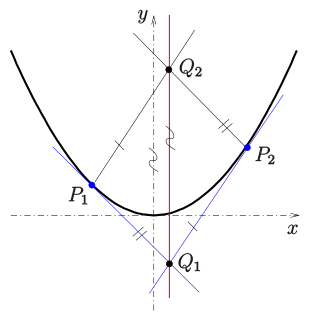
Bei der Punktkonstruktion und der Tangentenkonstruktion (s.o.) wird jeweils die Achsenrichtung der Parabel als bekannt vorausgesetzt. Ist die Achsenrichtung nicht bekannt, so lässt sie sich entweder

1) mit Hilfe der Mittelpunkte zweier paralleler Sehnen (s. oben) oder

2) mit Hilfe der folgenden Eigenschaft einer Parabel, die die Kenntnis zweier Parabelpunkte und deren Tangenten voraussetzt,

konstruieren.

Eine beliebige Parabel kann in einem geeigneten Koordinatensystem durch eine Gleichung y=ax^2 beschrieben werden.

Für eine Parabel y=ax^2 gilt: Sind

$P_1=(x_1,y_1),\, P_2=(x_2,y_2)$ zwei Punkte der Parabel,
$t_1,\, t_2$ die zugehörigen Tangenten,
der Schnittpunkt der beiden Tangenten $t_1,\, t_2$ ,
der Schnittpunkt der Parallele zu $t_{1}$ durch den Punkt $P_{2}$ mit der Parallele zu $t_{2}$ durch $P_{1}$ (s. Bild),

dann ist die Gerade Q_1Q_2 parallel zur Parabelachse und hat die Gleichung

$x={\tfrac {x_{1}+x_{2}}{2a}}.$

Zum Beweis: Wie bei den vorigen Parabeleigenschaften kann man den Beweis für die Normalparabel y=x^2 durchrechnen.

Bemerkung: Die hier beschriebene Eigenschaft ist eine affine Version der 3-Tangenten-Ausartung des Satzes von Brianchon.

Pol-Polare-Beziehung

Parabel: Pol-Polare-Beziehung

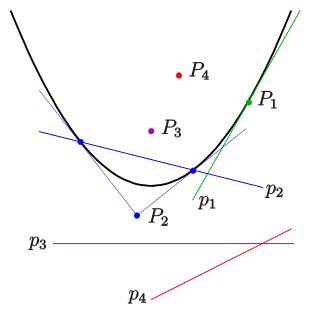
Eine Parabel lässt sich in einem geeigneten Koordinatensystem immer durch eine Gleichung der Form y=ax^2 beschreiben. Die Gleichung der Tangente in einem Parabelpunkt $P_{0}=(x_{0},y_{0}),y_{0}=ax_{0}^{2}$ ist y=2ax_0(x-x_0) + y_0=2ax_0x -ax^2_0=2ax_0x-y_0 . Lässt man im rechten Teil der Gleichung zu, dass P_0=(x_0,y_0) ein beliebiger Punkt der Ebene ist, so wird

dem Punkt

die Gerade y=2ax_0x - y_0

zugeordnet.

Und umgekehrt kann man

der Gerade y=mx+d

den Punkt $(\tfrac{m}{2a},-d)$ zuordnen.

So eine Zuordnung Punkt <-> Gerade nennt man eine Polarität oder Pol-Polare-Beziehung. Der Pol ist der Punkt, die Polare ist die zugehörige Gerade.

Die Bedeutung dieser Pol-Polare-Beziehung besteht darin, dass die möglichen Schnittpunkte der Polare mit der Parabel die Berührpunkte der Tangenten durch den Pol an die Parabel sind.

Liegt der Punkt (Pol) auf der Parabel, so ist seine Polare die Tangente in diesem Punkt (s. Bild: $P_1,\ p_1$ ).
Liegt der Pol außerhalb der Parabel, so sind die Schnittpunkte der Polare mit der Parabel die Berührpunkte der Tangenten durch den Pol an die Parabel (s. Bild: $P_2,\ p_2$ ).
Liegt der Punkt innerhalb der Parabel, so hat seine Polare keinen Schnittpunkt mit der Parabel (s. Bild: $P_3,\ p_3$ und $P_4,\ p_4$ ).

Zum Beweis: Die Bestimmung der Schnittpunkte der Polaren eines Punktes $(x_{0},y_{0})$ mit der Parabel y=ax^2 und die Suche nach Parabelpunkten, deren Tangenten den Punkt $(x_{0},y_{0})$ enthalten, führen auf dieselbe quadratische Gleichung.

Bemerkung:

Der Schnittpunkt zweier Polaren (z.B. im Bild: ) ist der Pol der Verbindungsgerade der zugehörigen Pole (hier: ).
Brennpunkt und Leitlinie sind zueinander polar.
Zur Parabelachse parallele Geraden haben keine Pole. Man sagt: „Ihre Pole liegen auf der Ferngeraden.“

Bemerkung: Pol-Polare-Beziehungen gibt es auch für Ellipsen und Hyperbeln. Siehe auch projektiver Kegelschnitt.

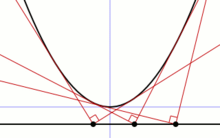
Parabel: zueinander orthogonale Tangenten

Orthogonale Tangenten

Eine Parabel besitzt folgende Eigenschaft:

Zueinander orthogonale Tangenten schneiden sich auf der Leitlinie.

Der geometrische Ort aller Punkte, in denen sich Tangenten einer gegebenen Kurve orthogonal schneiden, heißt Orthoptische Kurve. Bei einer Parabel ist also ihre Leitlinie die zugehörige orthoptische Kurve.

Fußpunktkurve

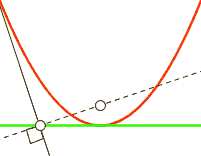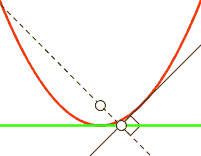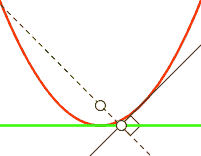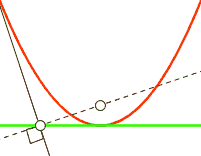
Fußpunktkurve einer Parabel bezüglich ihres Brennpunktes

Die Fußpunktkurve (engl.: pedal curve) einer (regulären) Kurve ist die Gesamtheit der Lotfußpunkte von einem festen Punkt aus auf die Tangenten der Kurve. Für eine Parabel gilt:

Die Fußpunktkurve einer Parabel bezüglich ihres Brennpunktes ist die Tangente im Scheitel.

Beweis:

Der Brennpunkt der Parabel y=ax^2 ist der Punkt $F=(0,{\tfrac {1}{4a}})$ . Die Tangente in einem beliebigen Parabelpunkt $(x_{0},ax_{0}^{2})$ hat die Gleichung

$y=2ax_{0}x-ax_{0}^{2}.$

Für $x_{0}=0$ ist die Behauptung richtig, sodass im Folgenden $x_{0}\neq 0$ vorausgesetzt werden kann.
Das Lot vom Brennpunkt aus auf die Tangente hat die Gleichung

$y=-{\frac {x}{2ax_{0}}}+{\frac {1}{4a}}\quad \leftrightarrow \quad 2ax_{0}x-ax_{0}^{2}=-(2ax_{0})^{2}y.$

Für den Schnittpunkt der Tangente mit dem Lot muss also

$y=-(2ax_{0})^{2}y$

erfüllt sein, was nur für y=0 möglich ist.

Parabeln der Form y=ax²+bx+c

Peripheriewinkelsatz für Parabeln

Parabeln der Form y=ax^2+bx+c sind Funktionsgraphen, die durch die 3 Parameter a,b,c eindeutig bestimmt sind. Man benötigt also 3 Punkte, um diese Parameter zu ermitteln. Eine schnelle Methode beruht auf dem Peripheriewinkelsatz für Parabeln.

Parabel: Peripheriewinkelsatz

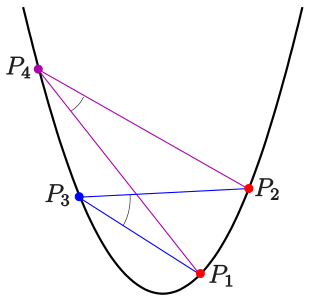
Um einen Winkel zwischen zwei Sehnen zu messen führen wir für zwei Geraden, die nicht zur -Achse parallel sind, ein Winkelmaß ein:

Für zwei Geraden $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2}$ messen wir den zu gehörigen Winkel mit der Zahl m_1-m_2

Zwei Geraden sind parallel, wenn m_1=m_2 und damit das Winkelmaß =0 ist.

Analog zum Peripheriewinkelsatz für Kreise gilt hier der

Peripheriewinkelsatz (für Parabeln):

Für vier Punkte $P_{i}=(x_{i},y_{i}),\ i=1,2,3,4,\ x_{i}\neq x_{k},i\neq k$ (s. Bild) gilt:

Die vier Punkte liegen nur dann auf einer Parabel der Form y=ax^2+bx+c

, wenn die Winkel bei $P_{3}$ und $P_{4}$ im obigen Winkelmaß gleich sind, d.h., wenn

${\frac {(y_{4}-y_{1})}{(x_{4}-x_{1})}}-{\frac {(y_{4}-y_{2})}{(x_{4}-x_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}-{\frac {(y_{3}-y_{2})}{(x_{3}-x_{2})}}.$

(Beweis durch Nachrechnen. Dabei kann man für die eine Richtung voraussetzen, dass die Punkte auf einer Parabel y=ax^2 liegen.)

3-Punkte-Form einer Parabel

Analog zur 2-Punkteform einer Gerade (Steigungswinkel werden mit der Steigung gemessen) folgt aus dem Peripheriewinkelsatz für Parabeln die

3-Punkte-Form (für Parabeln):

Die Gleichung der Parabel durch 3 Punkte $P_{i}=(x_{i},y_{i}),\ i=1,2,3,\ x_{i}\neq x_{k},i\neq k$ ergibt sich durch Auflösen der Gleichung

IMG class="text" style="width: 47.68ex; height: 6.5ex; vertical-align: -2.67ex;" alt="{\displaystyle {\frac {({\color {red}y}-y_{1})}{({\color {green}x}-x_{1})}}-{\frac {({\color {red}y}-y_{2})}{({\color {green}x}-x_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}-{\frac {(y_{3}-y_{2})}{(x_{3}-x_{2})}}}" src="/svg/ff43de0cd5dcad067288c1874ef71deca9b9ee1c.svg">

nach y.

Parabel in Polarkoordinaten

Eine Parabel, die in kartesischen Koordinaten durch y^2=4fx beschrieben ist, erfüllt in Polarkoordinaten die Gleichung

$r(\varphi) = 4f \frac{\cos(\varphi)}{\sin^2(\varphi)} \quad \text{mit} \varphi \in \left[ -\tfrac{\pi}{2} , \tfrac{\pi}{2} \right] \setminus\{0\}.$

Ihr Brennpunkt ist (f,0) . Legt man den Koordinatenursprung in ihren Brennpunkt, gilt für sie die polare Gleichung

$r(\varphi) = \frac{2f}{1-\cos(\varphi)}\text{ mit }\varphi \ne 2\pi k.$

Graphische Multiplikation

Graphische Multiplikation von 2 und 3 mithilfe einer Normalparabel

Eine Normalparabel ist eine „Multiplikationsmaschine“: Man kann mit ihr auf graphischem Wege das Produkt zweier Zahlen berechnen. Dazu zeichnet man zunächst die Normalparabel $y=x^{2}$ in ein kartesisches Koordinatensystem ein. Die zu multiplizierenden Faktoren trägt man auf der -Achse ab und bestimmt für jeden Wert einen Punkt auf der Parabel. Sind die Zahlen mit und bezeichnet, ergeben sich also zwei Punkte P(a|a^2) und Q(b|b^2) . Die Gerade durch und schneidet die -Achse in einem Punkt, dessen -Koordinate den Wert $-a \cdot b$ hat. Im Grenzfall a=b ergibt sich die Gerade als Tangente an die Parabel.

Falls und gleiches Vorzeichen haben, ist es praktikabler, einen der Faktoren in negativer Richtung aufzutragen anstatt später das Vorzeichen des Ergebnisses umzudrehen, so geschehen im Beispiel mit den Werten a=3 und b=2 . Hier trägt man die Faktoren als -Werte mit unterschiedlichen Vorzeichen in das Koordinatensystem ein, nämlich als P(-3|9) und Q(2|4) . Verbindet man die Punkte durch eine Gerade, so erkennt man, dass der Schnittpunkt der Geraden mit der -Achse gleich 6 = 2·3 ist.

Parabel und Kettenlinie

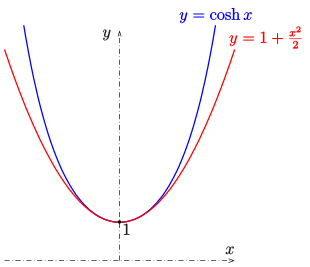
Approximation von cosh durch eine Parabel (rot)

Kettenlinien ähneln Parabeln, sind aber keine. Das Seil einer Hängebrücke, das durch sein Eigengewicht durchhängt, beschreibt eine Kettenlinie. Diese wird nicht durch eine quadratische Funktion, sondern durch den Kosinus hyperbolicus beschrieben. Mathematisch drückt sich die Ähnlichkeit dadurch aus, dass der Kosinus hyperbolicus sich in die Reihe

$\cosh x = \sum_{n=0}^\infty \frac{x^{2n}} {(2n)!} = {\color{red}1+ \frac{x^2}{2}} + \frac{x^4}{24} + \frac{x^6}{720} + \dots$

entwickeln lässt. Die ersten beiden Terme (rot) beschreiben eine Parabel und können als Approximation der cosh-Funktion für kleine verwendet werden.

Parabeln als quadratische Bézierkurven

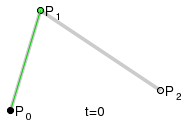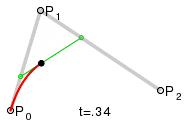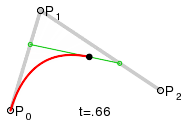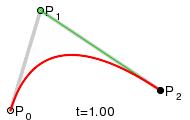
Konstruktion einer quadratischen Bézierkurve

Eine quadratische Bézierkurve ist eine Kurve, deren Parameterdarstellung $\vec c(t)$ durch drei Punkte $P_0:\vec p_0$ , $P_1:\vec p_1$ und $P_2:\vec p_2$ bestimmt wird:

$\begin{align} \vec c(t) \ & =\ \sum_{i=0}^2 \binom 2 i t^i (1-t)^{2-i} \vec p_i \\ \ & =\ (1 - t)^{2}\vec p_0 + 2t(1 - t)\vec p_1 + t^{2}\vec p_2 \\ \ & =\ (\vec p_0 - 2\vec p_1 + \vec p_2)t^{2} + (-2\vec p_0 + 2\vec p_1)t + \vec p_0 \text{ , } t \in [0,1] \end{align}$

Diese Kurve ist ein Parabelbogen (s. Abschnitt: Parabel als affines Bild der Normalparabel).

Parabeln und numerische Integration

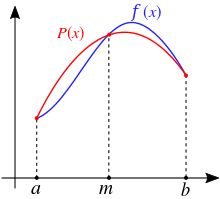
Simpson-Regel: Parabelbogen ersetzt Kurventeil

Bei der numerischen Integration nähert man den Wert eines bestimmten Integrals dadurch an, dass man den Graphen der zu integrierenden Funktion durch Parabelbögen annähert und integriert diese. Dies führt zur Simpsonregel, siehe Bild.

$\int_{a}^{b}f(x)\,dx \approx \frac{b-a}{6} \cdot \left( f(a)+4f \left( \frac{a+b}{2} \right)+f(b) \right)$

Die Güte der Approximation wird dadurch erhöht, dass man die Unterteilung vergrößert und den Graphen durch entsprechend viele Parabelbögen ersetzt und diese integriert.

Parabeln als ebene Schnitte von Quadriken

Folgende Flächen zweiter Ordnung (Quadriken) besitzen Parabeln als ebene Schnitte:

Elliptischer Kegel (siehe auch Kegelschnitt)
Parabolischer Zylinder
Elliptisches Paraboloid
Hyperbolisches Paraboloid
Einschaliges Hyperboloid
Zweischaliges Hyperboloid

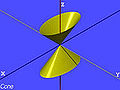Elliptischer Kegel
Parabolischer Zylinder
Elliptisches Paraboloid
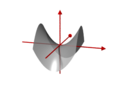Hyperbolisches Paraboloid
Einschaliges Hyperboloid
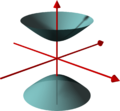Zweischaliges Hyperboloid

Laguerre-Ebene: Geometrie der Parabeln

Eine Laguerre-Ebene ist im klassischen Fall eine Inzidenzstruktur, die im Wesentlichen die Geometrie der Kurven y=ax^2+bx+c , das sind Parabeln und Geraden, in der reellen Anschauungsebene beschreibt. Als Verbindungskurven stehen hier nicht nur Geraden, sondern auch Parabeln zur Verfügung. Z.B. gibt es in einer Laguerre-Ebene zu drei Punkten mit verschiedenen x-Koordinaten genau eine solche Verbindungskurve.

Parabel als Trisektrix

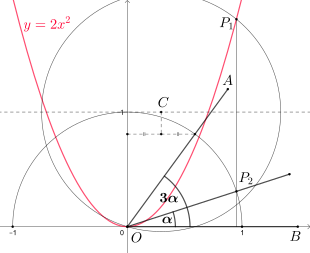
Exakte Winkeldrittelung mit einer Parabel

Eine Parabel lässt sich auch als Trisektrix verwenden, das heißt mit ihr als zusätzlichem Hilfsmittel ist die exakte Dreiteilung beliebiger Winkel mit Zirkel und Lineal möglich. Man beachte, dass dies nicht im Widerspruch zur Unmöglichkeit Winkeldreiteilung mit Zirkel und Lineal steht, da nach den klassischen Regeln für Konstruktionen mit Zirkel und Lineal die Verwendung von Parabeln nicht erlaubt ist.

Um einen $\angle AOB$ zu dritteln, platziert man seinen Schenkel $OB$ auf der x-Achse, so dass der Scheitel im Ursprung des Koordinatensystems liegt. Das Koordinatensystem enthält außerdem den Graph der Parabel $y=2x^{2}$ . Vom Schnittpunkt des Einheitskreises um den Ursprung mit dem zweiten Winkelschenkel $OA$ fällt man das Lot auf die y-Achse. Die Mittelsenkrechte des Lots und die Tangente an den Einheitskreis im Punkt (0,1) schneiden sich in einem Punkt . Dann schneidet der Kreis um mit Radius $|OC|$ die Parabel in $P_{1}$ und das Lot von $P_{1}$ auf die x-Achse schneidet den Einheitskreis in $P_{2}$ . Der Winkel $\angle BOP_{2}$ beträgt nun exakt ein Drittel des Ausgangswinkels $\angle AOB$ .

Die Korrektheit dieser Konstruktion kann man nachweisen, indem man zeigt, dass die x-Koordinate von $P_{1}$ den Wert $\cos(\alpha)$ besitzt. Das Gleichungssystem bestehend aus der Gleichung des Kreises um C und der Parabel liefert für die x-Koordinate von $P_{1}$ die kubische Gleichung $4x^{3}-3x-\cos(3\alpha )=0$ . Anhand der trigonometrischen Identität $\cos(3\alpha )=4\cos(\alpha )^{3}-3\cos(\alpha )$ sieht man nun sofort, dass $\cos(\alpha)$ eine Lösung der kubischen Gleichung ist.

Diese Art der Winkeldreiteilung geht auf René Descartes zurück, der sie in seinem Buch La Geometria (1637) beschrieb.

Parabel höherer Ordnung

Unter einer Parabel der Ordnung versteht man den Graph eines Polynoms $y=ax^{n}+\dotsc$ (im Gegensatz zu den Graphen von e-Funktion oder Wurzelfunktion, …). Eine Parabel 3. Ordnung wird auch kubische Parabel genannt.

Also: nur im Fall n=2 ist eine Parabel höherer Ordnung eine gewöhnliche Parabel.

Neilsche Parabel

Die Neilsche Parabel oder semikubische Parabel ist eine algebraische Kurve 3. Ordnung:

Kartesische Koordinatengleichung: $y^2 - a^2 x^3 \, = \, 0$ mit einem reellen Parameter
Explizit: $y = \pm a x^{\frac{3}{2}}$

Sie ist keine Parabel im üblichen Sinne; d.h. kein Kegelschnitt.

Parabel y=x² über einem beliebigen Zahlkörper

Betrachtet man in einer affinen Ebene über einem beliebigen (kommutativen) Körper die Punktmenge, die der Parabelgleichung y=x^2 genügt, so bleiben viele Eigenschaften der reellen Normalparabel, die mit „schneiden“, „verbinden“ und „parallel“ formuliert werden und deren Beweise nur Multiplikation/Division und Addition/Subtraktion verwenden, erhalten. Z.B.:

Eine Gerade schneidet die Parabel in höchstens zwei Punkten.
Durch jeden Parabelpunkt gibt es (neben der Geraden ) genau eine Gerade, die mit der Parabel nur den Punkt gemeinsam hat, die Tangente: . Eine Gerade ohne Schnittpunkt heißt Passante, eine mit zwei Schnittpunkten Sekante.

Unterschiede zum reellen Fall:

Für $K=\Q$ (rationale Zahlen) ist die Gerade eine Passante, denn die Gleichung hat in $\mathbb {Q}$ keine Lösung.
Für $K=\mathbb {C}$ (komplexe Zahlen) gibt es keine Passanten. Z.B.: schneidet die Parabel in den Punkten .
Hat der Körper die Charakteristik 2 (d.h., es gilt ), so gibt es unter den Geraden keine Sekanten, da jede Gleichung im Fall Charakteristik 2 höchstens eine Lösung hat (es gibt kein „ $\pm$ “). Die Tangente im Parabelpunkt hat (bei Charakteristik 2) die Gleichung . D.h., alle Tangenten sind parallel zur -Achse.

Siehe auch

Konfokale Kegelschnitte

Basierend auf einem Artikel in:

Wikipedia.de