Satz von Brianchon

Satz von Brianchon

Der Satz von Brianchon, benannt nach dem französischen Mathematiker Charles Julien Brianchon (1783–1864), ist ein klassischer Lehrsatz der ebenen Geometrie.

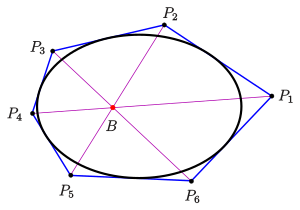
In einem konvexen Sechseck $P_{1}P_{2}P_{3}P_{4}P_{5}P_{6}$ , das einen nicht ausgearteten Kegelschnitt umschreibt (d.h. alle Seiten sind Tangenten des Kegelschnitts), schneiden sich die Diagonalen $P_{1}P_{4},P_{2}P_{5},P_{3}P_{6}$ in einem Punkt , dem Brianchon-Punkt.

Es handelt sich hier um die duale Version des Satzes von Pascal.

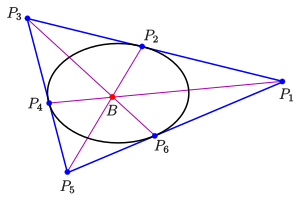
3-Tangenten-Ausartung des Satzes von Brianchon

Wie beim Satz von Pascal gibt es für den Satz von Brianchon auch Ausartungen. Dabei lässt man benachbarte Tangenten zusammenfallen und deren Schnittpunkt wird zu einem Kegelschnittpunkt. Bei dem Beispiel im Bild sind 3 Paare von Tangenten zusammengefallen. Dabei entsteht eine Aussage über Inellipsen von Dreiecken. Aus projektiver Sicht kann man weiterhin feststellen: Die beiden Dreiecke $P_{1}P_{3}P_{5}$ und $P_{2}P_{4}P_{6}$ liegen perspektiv. D.h. es gibt eine Zentralkollineation, die das eine Dreieck auf das andere Dreieck abbildet. Nur in Sonderfällen ist diese Zentralkollineation auch eine affine Abbildung (Streckung an einem Punkt), z.B. bei einer Steiner-Inellipse sind beide Dreiecke über eine Streckung am Mittelpunkt, der auch Brianchon-Punkt ist, miteinander verbunden.

Basierend auf einem Artikel in:

Wikipedia.de