Steiner-Inellipse

Die Steiner-Inellipse

In der Geometrie ist die Steiner-Inellipse eines Dreiecks die eindeutig bestimmte Ellipse, die einem Dreieck einbeschrieben ist und die Seiten dieses Dreiecks in ihren Mittelpunkten berührt. Die Steiner-Inellipse ist ein Beispiel für eine Inellipse. Auch der Inkreis und die Mandart-Inellipse sind Inellipsen; sie berühren die Dreiecksseiten aber im Allgemeinen nicht in den Mittelpunkten – außer wenn es sich um ein gleichseitiges Dreieck handelt. Die Steiner-Inellipse wird Jakob Steiner zugeschrieben. Der Eindeutigkeitsnachweis wurde von Kalman geführt.

Die Steiner-Inellipse ist das Gegenstück zur Steiner-Umellipse (oft nur, so wie im Folgenden, Steiner-Ellipse genannt), die durch die Ecken des gegebenen Dreiecks geht und den Dreiecksschwerpunkt als Mittelpunkt hat.

Definition und Eigenschaften

Definition

Sind $M_{1},M_{2},M_{3}$ die Mittelpunkte der Seiten eines Dreiecks ABC , so heißt eine Ellipse durch $M_{1},M_{2},M_{3}$ , die die Seiten des Dreiecks ABC dort berührt, Steiner-Inellipse.

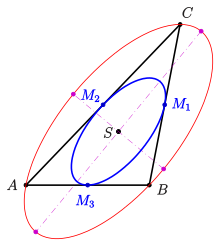
Steiner-Inellipse (blau) mit Steiner-Ellipse (rot)

Steiner-Inellipse (blau) und Steiner-Ellipse (rot) für ein gleichseitiges Dreieck

Eigenschaften:
Für ein beliebiges Dreieck ABC mit den Seitenmittelpunkten $M_{1},M_{2},M_{3}$ gilt:
a) Es gibt genau eine Steiner-Inellipse.
b) Der Mittelpunkt der Steiner-Inellipse ist der gemeinsame Schwerpunkt der Dreiecke ABC und $M_{1}M_{2}M_{3}$ . Damit ist die Steiner-Inellipse des Dreiecks ABC die Steiner-Ellipse des Dreiecks $M_{1}M_{2}M_{3}$ .
c) Die Steiner-Inellipse des Dreiecks ABC (im Bild blau) geht durch eine zentrische Streckung mit dem Faktor ${\tfrac 12}$ aus der Steiner-Ellipse (rot) hervor. Beide Ellipsen besitzen also dieselbe Exzentrizität (sind ähnlich).
d) Der Flächeninhalt der Steiner-Inellipse ergibt sich durch Multiplikation der Dreiecksfläche mit ${\tfrac {\pi }{3{\sqrt {3}}}}$ . Der Flächeninhalt beträgt ein Viertel des Inhalts der Steiner-Ellipse.
e) Die Steiner-Inellipse eines Dreiecks hat den größten Flächeninhalt unter allen einbeschriebenen Ellipsen des Dreiecks.

Beweis

Da ein beliebiges Dreieck durch eine affine Abbildung aus einem gleichseitigen Dreieck hervorgeht, eine affine Abbildung Mittelpunkte von Strecken und den Schwerpunkt eines Dreiecks auf die Mittelpunkte der Bildstrecken und den Schwerpunkt des Bilddreiecks sowie eine Ellipse und deren Mittelpunkt auf eine Ellipse und deren Mittelpunkt abbildet, genügt es, die Eigenschaften an einem gleichseitigen Dreieck nachzuweisen.
Zu a): Der Inkreis eines gleichseitigen Dreiecks berührt die Seiten in deren Mittelpunkten. Dies folgt entweder aus Symmetrieüberlegungen oder durch Nachrechnen. Es gibt keinen weiteren Kegelschnitt, der die Dreiecksseiten in den Seitenmittelpunkten berührt. Denn ein Kegelschnitt ist schon durch 5 Bestimmungsstücke (Punkte, Tangenten) eindeutig bestimmt.
Zu b): Nachrechnen
Zu c) Der Umkreis geht durch die Streckung mit dem Faktor $\tfrac 1 2$ am gemeinsamen Mittelpunkt in den Inkreis über. Die Exzentrizität ist eine Invariante bei einer Punktstreckung (Ähnlichkeitsabbildung).
Zu d): Verhältnisse von Flächen bleiben bei einer affinen Abbildung invariant.
Zu e): Siehe Inellipse oder Literatur.

Parameterdarstellung und Halbachsen

Parameterdarstellung:

Da die Steiner-Inellipse eines Dreiecks durch eine zentrisch Streckung mit dem Faktor ${\tfrac 12}$ aus der Steiner-Ellipse hervorgeht, erhält man die Parameterdarstellung (siehe Steiner-Ellipse):

${\vec {x}}={\vec {p}}(t)={\overrightarrow {OS}}\;+\;{\color {blue}{\frac {1}{2}}}{\overrightarrow {SC}}\;\cos t\;+\;{\frac {1}{{\color {blue}2}{\sqrt {3}}}}{\overrightarrow {AB}}\;\sin t\;,\quad 0\leq t<2\pi$

Die 4 Scheitel der Ellipse sind

${\vec {p}}(t_{0}),\;{\vec {p}}(t_{0}\pm {\frac {\pi }{2}}),\;{\vec {p}}(t_{0}+\pi ),$

wobei sich $t_{0}$ aus

$\cot(2t_{0})={\tfrac {{\vec {f}}_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}\quad$ mit $\quad {\vec {f}}_{1}={\frac {1}{2}}{\vec {SC}},\quad {\vec {f}}_{2}={\frac {1}{2{\sqrt {3}}}}{\vec {AB}}$

ergibt.

Halbachsen:

Mit den Abkürzungen

$M:={\color {blue}{\frac {1}{4}}}({\vec {SC}}^{2}+{\frac {1}{3}}{\vec {AB}}^{2})$

$N:={\frac {1}{{\color {blue}4}{\sqrt {3}}}}\left|\det({\vec {SC}},{\vec {AB}})\right|$

ergibt sich für die beiden Halbachsen $a,b,\;a>b$ :

$a={\frac {1}{2}}({\sqrt {M+2N}}+{\sqrt {M-2N}})$

$b={\frac {1}{2}}({\sqrt {M+2N}}-{\sqrt {M-2N}})$

Für die lineare Exzentrizität der Steiner-Inellipse ergibt sich daraus:

$e={\sqrt {a^{2}-b^{2}}}=\dotsb ={\sqrt {\sqrt {M^{2}-4N^{2}}}}$

Trilineare Gleichung, baryzentrische Gleichung

Die Gleichung der Steiner-Inellipse in trilinearen Koordinaten für ein Dreieck mit den Seitenlängen a,b,c ist:

$a^{2}x^{2}+b^{2}y^{2}+c^{2}z^{2}-2abxy-2bcyz-2cazx=0$

und in baryzentrischen Koordinaten

$\quad x^{2}+y^{2}+z^{2}-2(xy+yz+zx)=0\ .$

Alternative Berechnung der Halbachsen

Die Längen der großen und kleinen Halbachse für ein Dreieck mit Seitenlängen a,b,c sind

${\frac {1}{6}}{\sqrt {a^{2}+b^{2}+c^{2}\pm 2Z}}$

mit der Abkürzung

$Z:={\sqrt {a^{4}+b^{4}+c^{4}-a^{2}b^{2}-b^{2}c^{2}-c^{2}a^{2}}}.$

Eine Anwendung

Stellt man ein Dreieck in der komplexen Zahlenebene dar, das heißt, die Koordinaten seiner Eckpunkte entsprechen komplexen Zahlen, dann gilt für jedes Polynom dritten Grades, das diese Eckpunkte als Nullstellen besitzt, dass die Nullstellen seiner Ableitung die Brennpunkte der Steiner-Inellipse sind (Satz von Marden).

Konstruktionen

Für die Darstellung der Steiner-Inellipse genügen fünf generierte Punkte. Das beliebig gewählte Dreieck kann alternativ drei ungleich lange Seiten oder nur zwei gleiche Schenkel haben. In einem gleichseitiges Dreieck, das nach der modernen Definition ein Spezialfall des gleichschenkligen Dreiecks ist, ergeben die gleichen fünf Punkte den Inkreis des Dreiecks.

Die Steiner-Inellipse ist eine algebraische Kurve zweiten Grades. Mit Ausnahme des Kreises können solche Kurven nicht mit Zirkel und Lineal konstruiert werden. Es gibt aber für jede der beiden, im Folgenden beschriebenen, konstruktiven Methoden zur Ermittlung der entsprechenden fünf Ellipsenpunkte, Hilfsmittel, mit denen die Ellipsenlinie approximiert bzw. exakt gezeichnet werden kann.

Fünf Ellipsenpunkte

Bild 1: Steiner-Inellipse
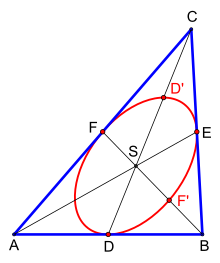
mit fünf konstruktiv bestimmten Punkten $D,F',E,D',F$

Im gewählten Dreieck ABC (Bild 1) mit drei ungleich langen Seiten werden die drei Seitenhalbierenden mit ihren Schnittpunkten $D,E$ und konstruiert. Sie treffen sich im Schwerpunkt der späteren Ellipse. Es folgt das Festlegen der Halbmesser ${\overline {SD'}}$ und ${\overline {SF'}}$ durch Verdoppelung der Strecken ${\overline {SD}}$ bzw. ${\overline {SD}}$ auf den Seitenhalbierenden innerhalb des Dreiecks. Die gesuchten fünf Ellipsenpunkte sind somit $D,F',E,D'$ und . Für das abschließende Zeichnen der Ellipsenlinie, je nachdem, ob die Konstruktion im Computer erfolgte oder mit Zirkel und Lineal erstellt wurde, finden folgende Hilfsmittel Verwendung:

Eine Dynamische-Geometrie-Software (DGS) zeichnet die Ellipse als (exakte) parametrisierte Kurve.
Verbindet man dagegen die fünf Ellipsenpunkte einfach mithilfe eines Kurvenlineals, erhält man eine approximierte Ellipse.

Haupt- und Nebenachse sowie Brennpunkte

Um in ein Dreieck mit drei ungleich langen Seiten das Zeichnen einer exakten Ellipsenlinie mithilfe eines mechanischen Hilfsmittels zu ermöglichen, bedarf es einer bzw. zweier der folgenden Gegebenheiten:

Haupt- und Nebenachse der Ellipse mit deren Scheitelpunkten $S_{1}\ldots S_{4},$ erforderlich bei Verwendung eines Ellipsographen
Brennpunkte der Ellipse $F_{1}$ und $F_{2},$ zusätzlich erforderlich bei Verwendung eines Ellipsenzirkels

Beide Voraussetzungen sind konstruierbar, wenn zuerst in dem gewählten Dreieck mindestens zwei sogenannte konjugierte Halbmesser der Inellipse, ähnlich der Konstruktion von konjugierten Halbmessern für die Steiner-Ellipse, bestimmt sind.

Vorgehensweise

Im gewählten Dreieck ABC (Bild 2) mit drei ungleich langen Seiten werden zwei Seitenhalbierende mit ihren Schnittpunkten $D_{1}$ und konstruiert. Sie treffen sich im Schwerpunkt der späteren Ellipse. Anschließend wird der erste relevante Halbmesser ${\overline {SD_{2}}}$ durch Verdoppelung der Strecke ${\overline {SD_{1}}}$ innerhalb des Dreiecks bestimmt. Es folgt die Scherung des Dreiecks ABC in ein gleichschenkliges und flächengleiches Dreieck A'B'C' mit (gleicher) Höhe ${\overline {D_{1}'C'}}$

Bild 2: Steiner-Inellipse
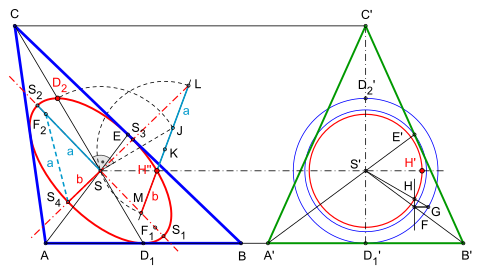
Links: Dreieck mit drei ungleich langen Seiten, mittig der Schwerpunkt Haupt- und Nebenachse mit den Scheitelpunkten $S_{1}\ldots S_{4}$ mithilfe der Rytz–Konstruktion (Punkte $J,K,L$ und ) bestimmt.
Rechts: Das durch Scherung erzeugte gleichschenklige Dreieck $A',B',C'$ mit den konjugierten Halbmessern $S,D_{2}'$ und $S,H',$ gemäß der Ellipsen-Konstruktion von de La Hire.

Es geht weiter im gleichschenkligen Dreieck mit der Seitenhalbierenden ${\overline {A'E'}},$ die im Schwerpunkt die Strecke ${\overline {D_{1}'C'}}$ schneidet, und der Verbindung mit $B'.$ Anschließend wird, gemäß der Ellipsen-Konstruktion von de La Hire, ein Kreis mit dem Radius ${\overline {S'E'}}$ um mit Schnittpunkt auf ${\overline {B'S'}}$ gezogen und eine Parallele zu ${\overline {AB'}}$ von durch gezeichnet. Der darauf folgende Kreis mit dem Radius ${\overline {S'D_{1}'}}$ um schneidet ${\overline {D_{1}'C'}}$ in $D_{2}'.$ Die nächste Parallele zu ${\overline {A'B'}}$ ab bis zum Kreis, der durch $D_{1}'$ verläuft, ergibt den Schnittpunkt der jetzt mit verbunden wird. Eine Parallele zu ${\overline {D_{1}'S'}}$ durch und durch die Strecke ${\overline {GS'}}$ ergibt darauf den Schnittpunkt der mithilfe des Kreises mit Radius ${\overline {S'H}}$ um auf die Schwerpunktachse ${\overline {SS'}}$ projiziert, mit ${\overline {S'H'}}$ den zweiten relevanten Halbmesser liefert. Somit sind die zwei konjugierten Halbmesser ${\overline {SD_{2}}}$ und ${\overline {S'H'}}$ ermittelt.

Die Weiterführung der Konstruktion erfolgt im gewählten Dreieck. Zuerst wird der soeben gefundene Halbmesser ${\overline {S'H'}}$ auf der Schwerpunktachse ${\overline {SS'}}$ ab mit Schnittpunkt $H''$ abgetragen. Die hiermit ermöglichte Konstruktion der Haupt- und Nebenachse der Ellipse wird anhand der sechs bildlich dargestellten Schritte der Rytzschen Achsenkonstruktion erstellt. Danach werden die beiden Brennpunkte $F_{1}$ und $F_{2}$ bestimmt, indem man den Halbmesser in den Zirkel nimmt, damit in den Scheitelpunkt $S_{3},$ oder wie dargestellt in $S_{4},$ einsticht und die Abstände $\left|S_{4}F_{1}\right|$ und $\left|S_{4}F_{2}\right|$ erzeugt.

Abschließend wird mithilfe eines Ellipsographen oder eines Ellipsenzirkels die Ellipsenlinie (exakt) eingezeichnet.

Alternative Konstruktion des zweiten Halbmessers

Bild 3: Steiner-Inellipse,
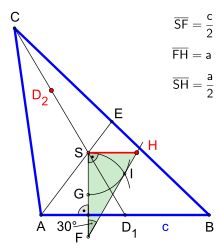
alternative Konstruktion des Halbmessers ${\overline {SH}}$ mithilfe des rechtwinkligen Dreiecks $SFH$

Zuerst erfolgt die Berechnung des Halbmessers ${\overline {SH}}.$ Als Ansatz dient die allgemeine Formel für die Höhe des gleichseitigen Dreiecks mit der Seite

$h={\frac {\sqrt {3}}{2}}\cdot a$

Die Hälfte dieses gleichseitigen Dreiecks ist ein rechtwinkliges Dreieck mit der (gleichen) Höhe:

$h={\frac {\sqrt {3}}{2}}\cdot 2\cdot {\frac {a}{2}}={\sqrt {3}}\cdot {\frac {a}{2}}$

Setzt man ${\overline {AB}}=c,$ ${\frac {a}{2}}={\overline {SH}},$ $a=2\cdot {\overline {SH}}$ und $h={\frac {c}{2}}$ ein, ergibt dies das rechtwinklige Dreieck $SFH$ (s. Bild 3) mit der Höhe

${\frac {c}{2}}={\sqrt {3}}\cdot {\overline {SH}},$

umgeformt gilt

${\overline {SH}}={\frac {1}{2}}\cdot {\frac {c}{\sqrt {3}}}.$

Es geht weiter mit der Konstruktion des rechtwinkligen Dreiecks $SFH:$

Sie beginnt mit dem Einzeichnen einer Senkrechten (Orthogonalen) zu ${\overline {AB}},$ ab dem Schwerpunkt und dem Übertragen der Strecke ${\overline {AD_{1}}}={\frac {c}{2}}$ auf die Senkrechte; es ergibt die Strecke ${\overline {SF}}.$ Nun folgt die Konstruktion der Winkelweite $30^{\circ }$ am Winkelscheitel indem man die Strecke ${\overline {SF}}$ in halbiert, einen Kreisbogen mit Radius ${\overline {GS}}$ um den Punkt und einen weiteren Kreisbogen mit derselben Zirkelöffnung um den Punkt zieht; dabei ergibt sich der Schnittpunkt $I.$ Durch das Einzeichnen einer Halbgeraden, ab durch , wird am Winkelscheitel der Winkel $30^{\circ }$ generiert. Die abschließende Parallele zur Strecke ${\overline {AB}},$ ab dem Schwerpunkt erzeugt den Schnittpunkt auf der Halbgeraden und liefert somit den gesuchten Halbmesser ${\overline {SH}}.$

Da dieses rechtwinklige Dreieck konstruktiv einfach darstellbar ist, besteht auch die Möglichkeit, auf diese Art und Weise den zweiten konjugierten Halbmesser ${\overline {SH}}$ zu finden.

Basierend auf einem Artikel in:

Wikipedia.de