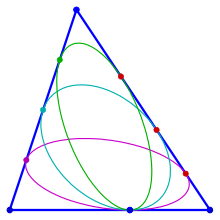
Inellipse

Beispiel einer Inellipse

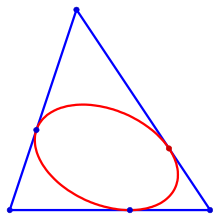
Eine Inellipse ist in der Geometrie eine Ellipse, die die Seiten eines gegebenen Dreiecks berührt. Das einfachste Beispiel ist der Inkreis. Weitere wichtige Beispiele sind die Steiner-Inellipse, die die Dreiecksseiten in deren Mitte berührt, die Mandart-Inellipse und die Brocard-Inellipse. Sie spielen in der Dreiecksgeometrie eine Rolle. Schränkt man die Ellipse nicht durch spezielle Anforderungen ein, so gibt es zu einem Dreieck unendlich viele Inellipsen.

Da ein nicht ausgearteter Kegelschnitt durch 5 Bestimmungsstücke (Punkte, Tangenten) eindeutig bestimmt ist, darf man für eine Inellipse eines Dreiecks nur auf zwei Seiten auch die Berührpunkte vorgeben. Der Berührpunkt auf der 3. Seite ist dann dadurch schon eindeutig bestimmt.

Parameterdarstellungen, Mittelpunkt, konjugierte Halbmesser

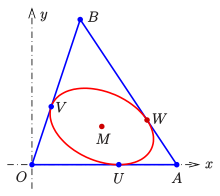
Eine Inellipse ist durch das Dreieck und die Vorgabe der zwei Berührpunkte

eindeutig bestimmt. (M = Mittelpunkt der Ellipse)

Die Inellipse des Dreiecks mit den Eckpunkten

$O=(0,0),\;A=(a_{1},a_{2}),\;B=(b_{1},b_{2})$

und den zwei Berührpunkten

$U=(u_{1},u_{2}),\;V=(v_{1},v_{2})$

auf der Seite $OA$ bzw. $OB$ lässt sich durch die rationale Parameterdarstellung

$\left({\frac {4u_{1}\xi ^{2}+v_{1}ab}{4\xi ^{2}+4\xi +ab}},{\frac {4u_{2}\xi ^{2}+v_{2}ab}{4\xi ^{2}+4\xi +ab}}\right)\ ,\ -\infty <\xi <\infty \ ,$

beschreiben. Dabei sind a,b durch die Vorgaben der Berührpunkte wie folgt bestimmt:

$a={\frac {1}{s-1}},\ u_{i}=sa_{i},\quad b={\frac {1}{t-1}},\ v_{i}=tb_{i}\;,\ 0<s,t<1\;.$

Der 3. Berührpunkt ist

$W=\left({\frac {u_{1}a+v_{1}b}{a+b+2}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+2}}\right)\;.$

Der Mittelpunkt der Inellipse ist

$M={\frac {ab}{ab-1}}\left({\frac {u_{1}+v_{1}}{2}},{\frac {u_{2}+v_{2}}{2}}\right)\;.$

Die Vektoren

${\vec {f}}_{1}={\frac {1}{2}}{\frac {\sqrt {ab}}{ab-1}}\;(u_{1}+v_{1},u_{2}+v_{2})$

${\vec {f}}_{2}={\frac {1}{2}}{\sqrt {\frac {ab}{ab-1}}}\;(u_{1}-v_{1},u_{2}-v_{2})\;$

sind zwei konjugierte Halbmesser und die Inellipse besitzt damit die weitere (übliche) Parameterdarstellung

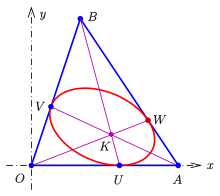
${\vec {x}}={\vec {OM}}+{\vec {f}}_{1}\cos \varphi +{\vec {f}}_{2}\sin \varphi \;.$

Brianchon-Punkt einer Inellipse eines Dreiecks

Der Brianchon-Punkt der Inellipse (gemeinsamer Punkt der Geraden ${\overline {AV}},{\overline {BU}},{\overline {OW}}$ ) ist

$K:\left({\frac {u_{1}a+v_{1}b}{a+b+1}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+1}}\right)\ .$

Mit Hilfe der Zahlen s,t lassen sich die zwei Berührpunkte U,V leicht variieren. Die Schranken für s,t sichern, dass die Berührpunkte wirklich auf den beiden Dreieckseiten liegen. Sie liefern für a,b die Schranken $-\infty <a,b<-1$ .

Man beachte, dass hier a,b nicht die Halbachsen der Ellipse oder Seiten des Dreiecks sind, sondern Parameter, die die Beziehung zwischen den Berührpunkten U,V und den Eckpunkten A,B festlegen !

Beispiele

Mandart-Inellipse

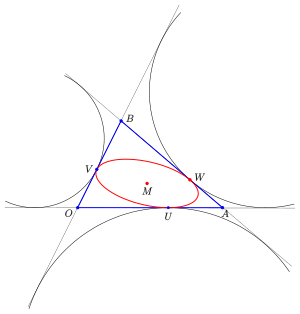
Steiner-Inellipse

Für $s=t={\tfrac {1}{2}}$ sind die Berührpunkte U,V,W die Seitenmitten und die Inellipse ist die Steiner-Inellipse (Mittelpunkt ist der Schwerpunkt).

Inkreis

Für $s={\tfrac {|OA|+|OB|-|AB|}{2|OA|}},\;t={\tfrac {|OA|+|OB|-|AB|}{2|OB|}}$ ergibt sich der Inkreis des Dreiecks mit dem Mittelpunkt

${\vec {OM}}={\tfrac {|OB|{\vec {OA}}+|OA|{\vec {OB}}}{|OA|+|OB|+|AB|}}\;.$

Mandart-Inellipse

Für $s={\tfrac {|OA|-|OB|+|AB|}{2|OA|}},\;t={\tfrac {-|OA|+|OB|+|AB|}{2|OB|}}$ erhält man die Mandart-Inellipse des Dreiecks. Sie berührt die Seiten in den Berührpunkten der Ankreise. Ihr Mittelpunkt ist der Mittenpunkt des Dreiecks.

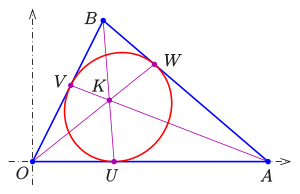
Brocard-Inellipse

Für $\ s={\tfrac {|OB|^{2}}{|OB|^{2}+|AB|^{2}}}\;,\quad t={\tfrac {|OA|^{2}}{|OA|^{2}+|AB|^{2}}}\;$ erhält man die Brocard-Inellipse. Sie ist durch die Vorgabe ihres Brianchon-Punktes in trilinearen Koordinaten $\ K:(|OB|:|OA|:|AB|)\$ eindeutig bestimmt.

Herleitungen

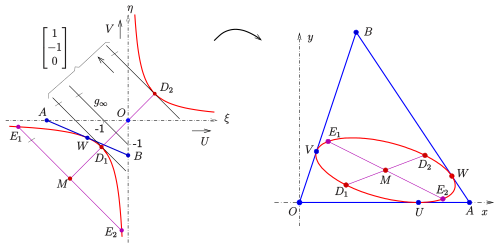
Bestimmung der Inellipse durch Lösen des Problems für eine Hyperbel in der $\xi -\eta -$ Ebene und anschließender Transformation der Lösung in die x-y-Ebene.
ist der Mittelpunkt der gesuchten Ellipse und $D_{1}D_{2},\;E_{1}E_{2}$ zwei konjugierte Durchmesser.
Sich entsprechende Punkte wurden in beiden Darstellungen mit denselben Buchstaben bezeichnet. $g_{\infty }$ ist die Ferngerade der x-y-Darstellung.

Neue Koordinaten

Zum Beweis betrachtet man die Aufgabe projektiv und führt geeignete neue inhomogene $\xi$ - $\eta$ -Koordinaten so ein, dass der gesuchte Kegelschnitt zur Hyperbel mit den Koordinatenachsen als Asymptoten wird und $U,V$ zu den Fernpunkten der Koordinatenachsen werden. Die Dreieckspunkte $A=(a_{1},a_{2}),\;B=(b_{1},b_{2})$ werden in den neuen Koordinaten (mit eckigen Klammern) durch $A=[a,0],B=[0,b]$ beschrieben und die Gerade dazu hat die Gleichung ${\frac {\xi }{a}}+{\frac {\eta }{b}}=1$ . (Dass die hier verwendeten a,b tatsächlich mit denen in der Aussage des Satzes identisch sind, zeigt die Rückabbildung unten.) Gesucht ist nun eine Hyperbel mit den Koordinatenachsen als Asymptoten, die die Gerade ${\overline {AB}}$ berührt. Man rechnet leicht nach, dass dies für die Hyperbel mit der Gleichung $\eta ={\frac {ab}{4\xi }}$ der Fall ist. Sie berührt die Gerade ${\overline {AB}}$ im Punkt $W=[{\tfrac {a}{2}},{\tfrac {b}{2}}]$ .

Koordinatentransformation

Die Rückabbildung der gefundenen Lösung wird in homogener Darstellung durch die Matrix

${\begin{bmatrix}u_{1}&v_{1}&0\\u_{2}&v_{2}&0\\1&1&1\end{bmatrix}}\quad$ beschrieben.

Ein Punkt $[x_{1},x_{2},x_{3}]$ wird dabei auf

${\begin{bmatrix}u_{1}&v_{1}&0\\u_{2}&v_{2}&0\\1&1&1\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}}={\begin{pmatrix}u_{1}x_{1}+v_{1}x_{2}\\u_{2}x_{1}+v_{2}x_{2}\\x_{1}+x_{2}+x_{3}\end{pmatrix}}\rightarrow \left({\frac {u_{1}x_{1}+v_{1}x_{2}}{x_{1}+x_{2}+x_{3}}}\;,\;{\frac {u_{2}x_{1}+v_{2}x_{2}}{x_{1}+x_{2}+x_{3}}}\right)\quad$ abgebildet, falls $x_{1}+x_{2}+x_{3}\neq 0$ ist. Ein Punkt $[\xi ,\eta ]$ der $\xi$ - $\eta$ -Ebene wird dabei durch den Spaltenvektor $[\xi ,\eta ,1]^{T}$ repräsentiert (siehe homogene Koordinaten). Ein Fernpunkt hat die Darstellung $[\cdots ,\cdots ,0]^{T}$ .

Koordinatentransformation wesentlicher Punkte

$U:\ [1,0,0]^{T}\ \rightarrow \ (u_{1},u_{2})\ ,\quad V:\ [0,1,0]^{T}\ \rightarrow \ (v_{1},v_{2})\ ,$

$O:\ [0,0]\ \rightarrow \ (0,0)\ ,\quad A:\ [a,0]\rightarrow \ (a_{1},a_{2})\ ,\quad B:\ [0,b]\rightarrow \ (b_{1},b_{2})\ ,$

(Man beachte, dass : $\ a={\tfrac {1}{s-1}},\ u_{i}=sa_{i},\quad b={\tfrac {1}{t-1}},\ v_{i}=tb_{i}\;$ ist.)

$g_{\infty }:\xi +\eta +1=0\$ ist Gleichung der Ferngerade der x-y-Ebene, Ihr Fernpunkt ist $[1,-1,0]^{T}$ .

$[1,-1,0]^{T}\ \rightarrow \ (u_{1}-v_{1},u_{2}-v_{2},0)^{T}$

Der Fernpunkt von $g_{\infty }$ in der $\xi$ - $\eta$ -Ebene geht also in einen Fernpunkt der x-y-Ebene über, den Fernpunkt der Gerade ${\overline {UV}}$ . Dies bedeutet: Die zwei in $\xi$ - $\eta$ -Koordinaten zu $g_{\infty }$ parallelen Tangenten der Hyperbel sind auch in den x-y-Koordinaten parallel. Die Berührpunkte dieser Tangenten sind:

$D_{i}:[{\frac {\pm {\sqrt {ab}}}{2}},{\frac {\pm {\sqrt {ab}}}{2}}]\ \rightarrow \ {\frac {1}{2}}{\frac {\pm {\sqrt {ab}}}{1\pm {\sqrt {ab}}}}\;(u_{1}+v_{1},u_{2}+v_{2}),\;$

Da in der x-y-Ebene die Ellipsentangenten in den Punkten $D_{1},D_{2}$ parallel sind, ist $D_{1}D_{2}$ ein Durchmesser der Ellipse, d.h. der Mittelpunkt der Strecke $D_{1}D_{2}$ ist der Mittelpunkt der Ellipse:

$M:\ {\frac {1}{2}}{\frac {ab}{ab-1}}\left(u_{1}+v_{1},u_{2}+v_{2}\right)\;$

Man prüft leicht nach, dass die $\xi$ - $\eta$ -Darstellung

$\ M:\;[{\frac {-ab}{2}},{\frac {-ab}{2}}]\$

hat. Um den zu $D_{1}D_{2}$ konjugierten Ellipsendurchmesser zu finden, muss man in der $\xi$ - $\eta$ -Ebene die Schnittpunkte E_1,E_2 der zu den Tangenten parallele Gerade durch (sie hat die Gleichung $\xi +\eta +ab=0$ ) mit der Hyperbel bestimmen. Es ergibt sich $E_{i}:\ [{\tfrac {-ab\pm {\sqrt {ab(ab-1)}}}{2}},{\tfrac {-ab\mp {\sqrt {ab(ab-1)}}}{2}}]\$ . Und in x-y-Koordinaten

$\ E_{i}={\frac {1}{2}}{\frac {ab}{ab-1}}\left(u_{1}+v_{1},u_{2}+v_{2}\right)\pm {\frac {1}{2}}{\frac {\sqrt {ab(ab-1)}}{ab-1}}\left(u_{1}-v_{1},u_{2}-v_{2}\right)\;,$

Aus den beiden konjugierten Durchmessern $D_{1}D_{2},E_{1}E_{2}$ lassen sich zwei vektorielle konjugierte Halbmesser ${\vec {f}}_{1},{\vec {f}}_{2}$ ermitteln:

${\vec {f}}_{1}={\vec {MD_{1}}}={\frac {1}{2}}{\frac {\sqrt {ab}}{ab-1}}\;(u_{1}+v_{1},u_{2}+v_{2})$

${\vec {f}}_{2}={\vec {ME_{1}}}={\frac {1}{2}}{\sqrt {\frac {ab}{ab-1}}}\;(u_{1}-v_{1},u_{2}-v_{2})\;.$

Damit ergibt sich eine trigonometrische Parameterdarstellung der Inellipse:

${\vec {x}}={\vec {OM}}+{\vec {f}}_{1}\cos \varphi +{\vec {f}}_{2}\sin \varphi \;.$

Hieraus lassen sich, wie bei der Steiner-Ellipse, die Halbachsen, Exzentrizität, der Flächeninhalt, die Scheitel und eine Gleichung in x-y-Koordinaten der Inellipse berechnen.

Für den Berührpunkt der Seite gilt:

$W:\ [{\frac {a}{2}},{\frac {b}{2}}]\ \rightarrow \ \left({\frac {u_{1}a+v_{1}b}{a+b+2}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+2}}\right)\;.$

Der Brianchon-Punkt der Inellipse ist der gemeinsame Punkt der drei Geraden ${\overline {AV}},{\overline {BU}},{\overline {OW}}$ . Man berechnet zunächst in der $\xi$ - $\eta$ -Ebene als Schnitt der drei Geraden: $\xi =a\;,\;\eta =b\;,\;a\eta -b\xi =0$ und transformiert den Schnittpunkt in die x-y-Ebene. Es ergibt sich

$K:\ [a,b]\ \rightarrow \ \left({\frac {u_{1}a+v_{1}b}{a+b+1}}\;,\;{\frac {u_{2}a+v_{2}b}{a+b+1}}\right)\ .$

Die punktweise Transformation der Hyperbel $\ \eta ={\frac {ab}{4\xi }}$ liefert eine rationale Parameterdarstellung der Inellipse:

$[\xi ,{\frac {ab}{4\xi }}]\ \rightarrow \ \left({\frac {4u_{1}\xi ^{2}+v_{1}ab}{4\xi ^{2}+4\xi +ab}},{\frac {4u_{2}\xi ^{2}+v_{2}ab}{4\xi ^{2}+4\xi +ab}}\right)\ ,\ -\infty <\xi <\infty \ .$

Inkreis

Inkreis eines Dreiecks

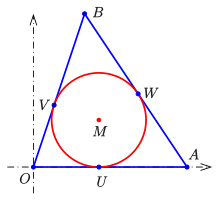
Für den Inkreis gilt $|OU|=|OV|$ und damit

(1) $\;s|OA|=t|OB|\;.\$ Ferner gilt in diesem Fall

(2) $\;(1-s)|OA|+(1-t)|OB|=|AB|$ . (s. Bild)

Löst man beide Gleichungen nach s,t auf, erhält man

(3) $\;s={\tfrac {|OA|+|OB|-|AB|}{2|OA|}},\;t={\tfrac {|OA|+|OB|-|AB|}{2|OB|}}\;.$

Um den Mittelpunkt zu bestimmen, berechnet man zunächst mit Hilfe von (1) und (3)

$1-1/ab=1-(s-1)(t-1)=-st+s+t=\cdots ={\tfrac {s}{2(|OB|}}(|OA|+|OB|+|AB|)\;.$

Also ist

${\vec {OM}}={\tfrac {|OB|}{s(|OA|+|OB|+|AB|)}}\;(s{\vec {OA}}+t{\vec {OB}})=\cdots ={\tfrac {|OB|{\vec {OA}}+|OA|{\vec {OB}}}{|OA|+|OB|+|AB|}}\;.$

Mandart-Inellipse

Die Parameter $s,t$ für die Mandart-Inellipse ergeben sich aus den Angaben für die Abstände der Berührpunkte der Ankreise (s. Ankreis) von den Ecken.

Brocard-Inellipse

Die Brocard-Inellipse wird durch die Vorgabe ihres Brianchon-Punktes festgelegt. Er hat in trilinearen Koordinaten die einfache Darstellung $\ K:(|OB|:|OA|:|AB|)\$ . Rechnet man die trilinearen Koordinaten in die hier geeignete Darstellung $\ K:k_{1}{\vec {OA}}+k_{2}{\vec {OB}}\$ um, so erhält man $\ k_{1}={\tfrac {|OB|^{2}}{|OB|^{2}+|OA|^{2}+|AB|^{2}}},\;k_{2}={\tfrac {|OA|^{2}}{|OB|^{2}+|OA|^{2}+|AB|^{2}}}\$ . Sind andererseits die Parameter s,t einer Inellipse vorgegeben, so ergibt sich aus der obigen Formel für , dass $\ k_{1}={\tfrac {s(t-1)}{st-1}},\;k_{2}={\tfrac {t(s-1)}{st-1}}\$ ist. Setzt man die Ausdrücke für $k_{1},k_{2}$ jeweils gleich und löst nach s,t auf, so ergibt sich

$s={\tfrac {|OB|^{2}}{|OB|^{2}+|AB|^{2}}}\;,\quad t={\tfrac {|OA|^{2}}{|OA|^{2}+|AB|^{2}}}\;.$

Inellipse mit maximalem Flächeninhalt

Die Steiner-Inellipse hat den größten Flächeninhalt von allen Inellipsen eines Dreiecks.

Nachweis

Aus einem Satz von Apollonios folgt, dass der Flächeninhalt einer Ellipse mit den konjugierten Halbmessern $\vec f_1,\vec f_2$ gleich

$F=\pi \left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|\quad$ ist (s. Artikel Steiner-Ellipse).

Für die Inellipse mit den Parametern s,t ist (s.o.)

$\det({\vec {f}}_{1},{\vec {f}}_{2})={\frac {1}{4}}{\frac {ab}{(ab-1)^{3/2}}}\det(s{\vec {a}}+t{\vec {b}},s{\vec {a}}-t{\vec {b}})$

$={\frac {1}{2}}{\frac {s{\sqrt {s-1}}\;t{\sqrt {t-1}}}{(1-(s-1)(t-1))^{3/2}}}\det({\vec {b}},{\vec {a}})\;.$

(Es ist ${\vec {a}}=(a_{1},a_{2}),\;{\vec {b}}=(b_{1},b_{2}),\;{\vec {u}}=(u_{1},u_{2}),{\vec {v}}=(v_{1},v_{2}),\;{\vec {u}}=s{\vec {a}},\;{\vec {v}}=t{\vec {b}}$ . Man beachte die Regeln für Determinanten !)
Um die Wurzeln bei der Berechnung zu vermeiden, genügt es, die Extremstellen der Funktion $G(s,t)={\tfrac {s^{2}(s-1)\;t^{2}(t-1)}{(1-(s-1)(t-1))^{3}}}$ zu bestimmen:

$G_{s}=0\ \rightarrow \ 3s-2+2(s-1)(t-1)=0\;.$

Wegen $G(s,t)=G(t,s)$ ergibt sich durch Vertauschen von s und t:

$G_{t}=0\ \rightarrow \ 3t-2+2(s-1)(t-1)=0\;.$

Auflösen der beiden Gleichungen nach s und t liefert

$s=t={\frac {1}{2}}\;,\quad$ d.h.:

Die Steiner-Inellipse ist die Inellipse mit maximalem Flächeninhalt.

Inellipse und baryzentrische Koordinaten

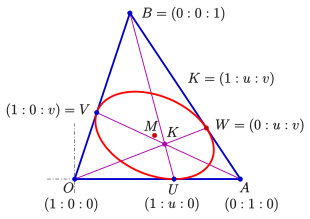
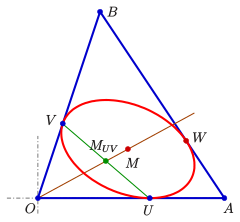
Inellipse und baryzentrische Koordinaten

Richtungen konjugierter Durchmesser und Mittelpunkt

Führt man für eine baryzentrische Beschreibung mit

$O=(1:0:0),\ A=(0:1:0),\ B=(0:0:1)$

Parameter u,v so ein, dass

$U=(1:u:0),\ V=(1:0:v)$ ist,

so gilt zwischen den obigen Parametern s,t und u,v

$u={\tfrac {s}{1-s}},\ v={\tfrac {t}{1-t}}\$ und umgekehrt $\ s={\tfrac {u}{1+u}},\ t={\tfrac {v}{1+v}}\ .$

Der 3. Berührpunkt ist dann : $\ W=(0:u:v)\$ und der Brianchonpunkt hat die einfache Darstellung

$K=(1:u:v)$

Hieran erkennt man, dass die Inellipse auch durch die Lage ihres Brianchonpunktes (und des Dreiecks) eindeutig beschrieben wird.

Der Mittelpunkt der Ellipse ist

$M={\big (}u+v:u(1+v):(1+u)v{\big )}\ .$

Dieses Ergebnis kann man aus der obigen Formel für den Mittelpunkt ableiten oder die Eigenschaft

Der Mittelpunkt $M_{UV}$ der Sehne U,V

liegt auf der Gerade ${\overline {OM}}$

verwenden. (Die Richtungen der Geraden ${\overline {OM}},{\overline {UV}}$ sind bezüglich der Ellipse konjugiert.) Diese Eigenschaft gilt entsprechend auch für $\overline{AM}$ und ${\overline {BM}}$ . kann also in baryzentrischen Koordinaten als Schnittpunkt der Geraden ${\overline {OM_{UV}}},{\overline {AM_{UW}}}$ berechnet werden. Aber auch die zeichnerische Bestimmung von ist damit möglich.

Der Vorteil der baryzentrischen Beschreibung besteht in ihrer Übersichtlichkeit. Die x-y-Koordinaten von Punkten lassen sich leicht aus ihren baryzentrischen Koordinaten mit der Schwerpunkt-Formel berechnen.

3 sich berührende Inellipsen in einem Dreieck

Basierend auf einem Artikel in:

Wikipedia.de