Konjugierte Durchmesser

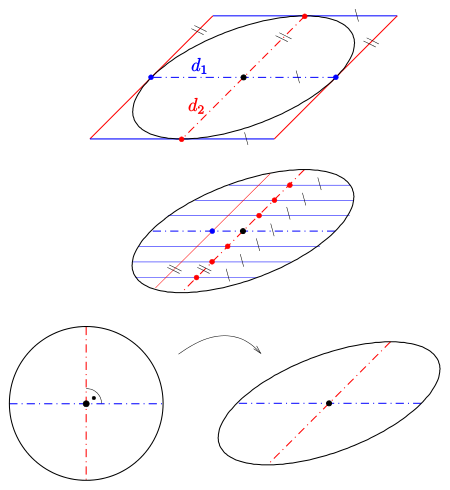
Definitionen konjugierter Durchmesser einer Ellipse:
oben: KD1, mitte: KD2, unten KD3

Konjugierte Durchmesser sind in der Geometrie zwei Durchmesser einer Ellipse, die in einer besonderen Beziehung zueinander stehen.

Dabei bedeutet Durchmesser eine Sehne durch den Mittelpunkt. Ist die Ellipse ein Kreis, so sind zwei Durchmesser genau dann konjugiert, wenn sie orthogonal sind.

In der Literatur findet man die folgenden äquivalenten Definitionen:

KD1: Die Tangenten in den Endpunkten eines Durchmessers $d_{1}$ einer Ellipse sind parallel. Ist $d_{2}$ der zu diesen Tangenten parallele Durchmesser, so gilt auch die Umkehrung: Die Tangenten in den Endpunkten von $d_{2}$ sind zu $d_{1}$ parallel.

Zwei Durchmesser d_1, d_2

einer Ellipse heißen konjugiert, wenn die Tangenten in den Endpunkten des einen Durchmessers parallel sind zum anderen Durchmesser.

KD2: Die Mittelpunkte der zu einem Durchmesser $d_{1}$ parallelen Sehnen einer Ellipse liegen auf einem Durchmesser $d_{2}$ . Und umgekehrt: Die Mittelpunkte der zu $d_{2}$ parallelen Sehnen liegen auf $d_{1}$ .

Zwei Durchmesser $d_{1},d_{2}$ heißen konjugiert, wenn die Mittelpunkte der zu $d_{1}$ parallelen Sehnen auf $d_{2}$ liegen.

KD3: Fasst man eine Ellipse als affines Bild des Einheitskreises auf, so heißen die Bilder orthogonaler Kreisdurchmesser konjugiert.

Der Beweis der Eigenschaften in KD1 und KD2 ergibt sich aus der Tatsache, dass eine beliebige Ellipse ein affines Bild des Einheitskreises ist. Denn die beiden Eigenschaften sind bei einem Kreis offensichtlich richtig, und eine affine Abbildung bildet Mittelpunkte auf Mittelpunkte ab und erhält die Parallelität.

Die Hauptachsen einer Ellipse sind immer konjugiert.

Zwei konjugierte Halbmesser einer Ellipse sind zwei auf verschiedenen zueinander konjugierten Durchmessern liegende halbe Durchmesser.
Zwei konjugierte Punkte einer Ellipse sind zwei auf verschiedenen zueinander konjugierten Durchmessern liegende Ellipsenpunkte.
Zwei Richtungen (Vektoren) heißen konjugiert, wenn es ein dazu paralleles Paar von konjugierten Durchmessern der Ellipse gibt.

Konjugierte Durchmesser spielen in der Darstellenden Geometrie bei der Rytzschen Achsenkonstruktion eine wichtige Rolle. Dabei werden aus der Kenntnis zweier konjugierter Halbmesser die Hauptachsen einer Ellipse rekonstruiert.

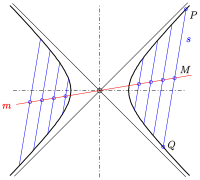Hyperbel: Mittelpunkte paralleler Sehnen
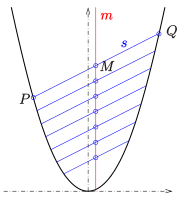Parabel: Mittelpunkte paralleler Sehnen

Bemerkung:

Die Mittelpunkte paralleler Sehnen einer Hyperbel liegen auch auf einer Gerade durch den Mittelpunkt. Diese Gerade muss aber keine Sehne sein, nämlich dann, wenn die parallelen Sehnen beide Äste der Hyperbel schneiden. Deshalb spricht man hier nur von konjugierten Richtungen. Wenn bei einer Hyperbel von konjugierten Durchmessern die Rede ist, ist mit Durchmesser ein Durchmesser der gegebenen Hyperbel oder der zu ihr konjugierten Hyperbel gemeint. (Die zur Hyperbel $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}=1$ konjugierte Hyperbel hat die Gleichung $-{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ .)
Die Mittelpunkte paralleler Sehnen einer Parabel liegen auch auf einer Gerade. Diese Gerade ist immer parallel zur Parabelachse (s. Bild). Da eine Parabel keinen Mittelpunkt besitzt, spricht man hier i.a. nicht von konjugierten Durchmessern. Manchmal wird eine Parallele zur Parabelachse als Durchmesser bezeichnet.

Berechnung konjugierter Punkte einer Ellipse

Die Tangente an die Ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ im Punkt (x_1,y_1) hat die Gleichung ${\frac {x_{1}x}{a^{2}}}+{\frac {y_{1}y}{b^{2}}}=1$ (siehe Ellipse). Ein zu konjugierter Punkt (x_2,y_2) muss auf der zur Tangente parallelen Gerade durch den Nullpunkt (Mittelpunkt) liegen. Also gilt

Zwei Punkte $(x_{1},y_{1}),(x_{2},y_{2})$ der Ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ sind genau dann konjugiert, wenn die Gleichung

${\frac {x_{1}x_{2}}{a^{2}}}+{\frac {y_{1}y_{2}}{b^{2}}}=0$

erfüllt ist.

Falls a=b , d.h. die Ellipse ein Kreis ist, gehören zwei konjugierte Punkte zwei orthogonalen Halbmessern an und die letzte Gleichung hat die vertraute Form $x_{1}x_{2}+y_{1}y_{2}=0$ (Skalarprodukt =0).

Ist die Ellipse durch die Parameterdarstellung

$x(t)=a\cos t,\quad y(t)=b\sin t$

gegeben d.h. als affines Bild des Einheitskreises $(\cos t,\sin t),\ 0\leq t<2\pi$ , so gehören die Punkte $(x(t),y(t),\ (x(t\pm {\tfrac {\pi }{2}}),y(t\pm {\tfrac {\pi }{2}})$ als Bilder von orthogonalen Halbmessern des Einheitskreises zu konjugierten Punkten der Ellipse. Mit Hilfe der Additionstheoreme folgt:

Die zwei Punkte $(-a\sin t,b\cos t),\ (a\sin t,-b\cos t)$ sind zum Punkt $(a\cos t,b\sin t)$ konjugiert.

Zusammenhang mit Orthogonalitätsrelationen

Der vorige Abschnitt hat gezeigt, dass die Ellipse $\tfrac{x^2}{a^2}+\tfrac{y^2}{b^2}=1$ direkt mit der symmetrischen Bilinearform

$\ f((x_{1},y_{1}),(x_{2},y_{2}))={\frac {x_{1}x_{2}}{a^{2}}}+{\frac {y_{1}y_{2}}{b^{2}}}$

zusammenhängt. Diese Bilinearform definiert

auf $\mathbb {R} ^{2}$ eine Orthogonalitätsrelation:

$(x_{1},y_{1}),(x_{2},y_{2})\neq (0,0)$ sind genau dann orthogonal, wenn $f((x_{1},y_{1}),(x_{2},y_{2}))={\frac {x_{1}x_{2}}{a^{2}}}+{\frac {y_{1}y_{2}}{b^{2}}}=0$ ist, und

auf $\mathbb {R} ^{2}$ eine Metrik:

$f((x,y),(x,y))={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}$ ist die Länge des Vektors (x,y)

und

auf der Ferngerade eine elliptische Polarität. (Elliptisch bedeutet hier: die Polarität hat keine Fixpunkte. Dies ist gleichbedeutend zu kein Vektor ist zu sich selbst orthogonal)

Zwei konjugierte Richtungen sind also orthogonal im hier definierten Sinne und die gegebene Ellipse ist der "Einheitskreis" bezüglich der hier definierten Metrik.

Bemerkung 1: Die Hyperbel $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}=1$ führt mit analogen Überlegungen auf die symmetrische Bilinearform

$\ f((x_{1},y_{1}),(x_{2},y_{2}))={\frac {x_{1}x_{2}}{a^{2}}}-{\frac {y_{1}y_{2}}{b^{2}}}$ .

Auch hier kann man eine Orthogonalitätsrelation und eine Metrik definieren. Das besondere in diesem Fall ist: Es gibt Richtungen, die zu sich selbst orthogonal sind, nämlich die Asymptotenrichtungen, und es gibt von (0,0) verschiedene Vektoren der Länge 0 ! Diese Metrik nennt man auch Minkowski-Metrik und die zugehörigen "Kreise" (=Hyperbeln) Minkowski-Kreise oder pseudoeuklidische Kreise. Dieser Fall spielt in der Relativitätstheorie eine wesentliche Rolle. Auf der Ferngerade induziert die Bilinearform eine hyperbolische Polarität. (Hyperbolisch bedeutet hier: Die Polarität hat zwei Fixpunkte.)

Bemerkung 2: Versucht man analoge Überlegungen für eine Parabel, so führt dies auf eine "unbrauchbare" Orthogonalitätsrelation. In diesem Fall wären nämlich alle Richtungen zur Richtung der Parabelachse orthogonal.

Siehe auch

Satz von Apollonios

Basierend auf einem Artikel in:

Wikipedia.de