Formelsammlung Trigonometrie
Dreieckberechnung
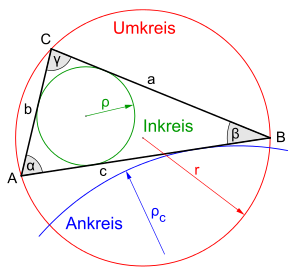
Die folgende Liste enthält die meisten bekannten Formeln aus der Trigonometrie in der Ebene. Die meisten dieser Beziehungen verwenden trigonometrische Funktionen.
Dabei werden die folgenden Bezeichnungen verwendet: Das Dreieck
habe die Seiten
,
und
,
die Winkel
,
und
bei den Ecken
,
und
.
Ferner seien
der Umkreisradius,
der Inkreisradius und
,
und
die Ankreisradien (und zwar die
Radien der Ankreise, die den Ecken
,
bzw.
gegenüberliegen) des Dreiecks
.
Die Variable
steht für den halben Umfang des Dreiecks
:
.
Schließlich wird die Fläche des Dreiecks
mit
bezeichnet. Alle anderen Bezeichnungen werden jeweils in den entsprechenden
Abschnitten, in denen sie vorkommen, erläutert.
Es ist zu beachten, dass hier die Bezeichnungen für den Umkreisradius ,
den Inkreisradius
und die drei Ankreisradien
,
,
benutzt werden. Oft werden davon abweichend für dieselben Größen auch die
Bezeichnungen
,
,
,
,
verwendet.
Winkelsumme
Sinussatz
Formel 1:
Formel 2:
wenn
wenn
wenn
Kosinussatz
Formel 1:
Formel 2:
wenn
wenn
wenn
Projektionssatz
Die Mollweideschen Formeln
Tangenssatz
Formel 1:
Analoge Formeln gelten für
und
:
Wegen
bleibt eine dieser Formel gültig, wenn sowohl die Seiten als auch die
zugehörigen Winkel vertauscht werden, also etwa:
Formel 2:
wenn
wenn
wenn
Formeln mit dem halben Umfang
Im Folgenden bedeutet
immer die Hälfte des Umfangs des Dreiecks
,
also
.
Flächeninhalt und Umkreisradius
Der Flächeninhalt des Dreiecks wird hier mit
bezeichnet (nicht, wie heute üblich, mit
,
um eine Verwechselung mit der Dreiecksecke
auszuschließen):
Weitere Flächenformeln:
, wobei
,
und
die Längen der von
,
bzw.
ausgehenden Höhen des Dreiecks
sind.
, mit
Erweiterter Sinussatz:
In- und Ankreisradien
In diesem Abschnitt werden Formeln aufgelistet, in denen der
Inkreisradius
und die Ankreisradien
,
und
des Dreiecks
vorkommen.
Wichtige Ungleichung: ;
Gleichheit tritt nur dann ein, wenn Dreieck
gleichseitig ist.
Die Ankreise sind gleichberechtigt: Jede Formel für
gilt in analoger Form für
und
.
Höhen
Die Längen der von ,
bzw.
ausgehenden Höhen des Dreiecks
werden mit
,
und
bezeichnet.
Hat das Dreieck
einen rechten Winkel bei
(ist also
),
dann gilt
Seitenhalbierende
Die Längen der von ,
bzw.
ausgehenden Seitenhalbierenden des Dreiecks
werden
,
und
genannt.
Winkelhalbierende
Wir bezeichnen mit ,
und
die Längen der von
,
bzw.
ausgehenden Winkelhalbierenden im Dreieck
.
Allgemeine Trigonometrie in der Ebene
Periodizität
Gegenseitige Darstellung
Die trigonometrischen Funktionen lassen sich ineinander umwandeln oder gegenseitig darstellen. Es gelten folgende Zusammenhänge:
(Siehe auch den Abschnitt Phasenverschiebungen.)
Mittels dieser Gleichungen lassen sich die drei vorkommenden Funktionen durch eine der beiden anderen darstellen:
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für | ||
| für |
Vorzeichen der Winkelfunktionen
Die Vorzeichen
von ,
und
stimmen überein mit denen ihrer Kehrwertfunktionen
,
bzw.
.
Wichtige Funktionswerte

Es sind noch viele weitere Werte darstellbar.
Symmetrien
Die trigonometrischen Funktionen haben einfache Symmetrien:
Phasenverschiebungen
Rückführung auf spitze Winkel
Darstellung durch den Tangens des halben Winkels
Mit der Bezeichnung
gelten die folgenden Beziehungen für beliebiges
Additionstheoreme
Für Sinus und Kosinus lassen sich die Additionstheoreme aus der Verkettung
zweier Drehung um den Winkel
bzw.
herleiten. Das ist elementargeometrisch möglich; sehr viel einfacher ist das
koordinatenweise Ablesen der Formeln aus dem Produkt
zweier Drehmatrizen der Ebene
.
Alternativ folgen die Additionstheoreme aus der Anwendung der Eulerschen
Formel auf die Beziehung
.
Die Ergebnisse für das Doppelvorzeichen ergeben sich durch Anwendung der Symmetrien.
Durch Erweiterung mit
bzw.
und Vereinfachung des Doppelbruchs:
Für
folgen hieraus die Doppelwinkelfunktionen,
für
die Phasenverschiebungen.
Additionstheoreme für Arkusfunktionen
Für die Arkusfunktionen gelten folgende Additionstheoreme
| Summanden | Summenformel | Gültigkeitsbereich |
|---|---|---|
Doppelwinkelfunktionen
Winkelfunktionen für weitere Vielfache
Die Formeln für Vielfache berechnen sich normalerweise über die komplexen
Zahlen aus der Euler-Formel
und der DeMoivre-Formel
.
Damit ergibt sich
.
Zerlegung in Real- und Imaginärteil liefert dann die Formeln für
und
bzw. die allgemeine Reihendarstellung.
Die Formel für
steht über
mit den Tschebyschow-Polynomen
in Beziehung.
Halbwinkelformeln
Zur Berechnung des Funktionswertes des halben Arguments dienen die Halbwinkelformeln, welche sich mittels Substitution aus den Doppelwinkelformeln herleiten lassen:
Außerdem gilt:
Siehe auch: Halbwinkelsatz
Summen zweier trigonometrischer Funktionen (Identitäten)
Aus den Additionstheoremen lassen sich Identitäten ableiten, mit deren Hilfe die Summe zweier trigonometrischer Funktionen als Produkt dargestellt werden kann:
Daraus ergeben sich noch Spezialfälle:
Produkte der Winkelfunktionen
Produkte der trigonometrischen Funktionen lassen sich mit folgenden Formeln berechnen:
Aus der Doppelwinkelfunktion
für
folgt außerdem:
Potenzen der Winkelfunktionen
Sinus
Kosinus
Tangens
Umrechnung in andere trigonometrische Funktionen
Weitere Formeln für den Fall α + β + γ = 180°
Die folgenden Formeln gelten für beliebige ebene Dreiecke und folgen nach
längeren Termumformungen aus ,
solange die in den Formeln vorkommenden Funktionen wohldefiniert sind (Letzteres
betrifft nur die Formeln, in denen Tangens und Kotangens vorkommen).
Sinusoid und Linearkombination mit gleicher Phase
wobei
Allgemeiner ist
wobei
und
Ableitungen und Stammfunktionen
Reihenentwicklung
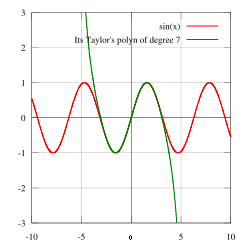
Wie auch sonst in der Analysis werden alle Winkel im Bogenmaß angegeben.
Man kann zeigen, dass der Kosinus die Ableitung
des Sinus darstellt und die Ableitung des Kosinus der negative Sinus ist. Hat
man diese Ableitungen, kann man die Taylorreihe
entwickeln (am einfachsten mit dem Entwicklungspunkt )
und zeigen, dass die folgenden Identitäten für alle
aus den reellen
Zahlen gelten. Mit diesen Reihen werden die trigonometrischen Funktionen für
komplexe Argumente
definiert (
bzw.
bezeichnet dabei die Bernoulli-Zahlen):
Produktentwicklung
Zusammenhang mit der komplexen Exponentialfunktion
Ferner besteht zwischen den Funktionen ,
und der komplexen
Exponentialfunktion
folgender Zusammenhang:
Weiterhin wird
geschrieben.
Auf Grund der oben genannten Symmetrien gilt weiter:
Mit diesen Beziehungen können einige Additionstheoreme besonders einfach und elegant hergeleitet werden.
Sphärische Trigonometrie
Eine Formelsammlung für das rechtwinklige und das allgemeine Dreieck auf der Kugeloberfläche findet sich in einem eigenen Kapitel.
Literatur
- I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik. 19. Auflage, 1979. B.G. Teubner Verlagsgesellschaft, Leipzig.
- I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products Academic Press, 5th edition (1994). ISBN 0-12-294755-X


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.01. 2022