
Arkusfunktion
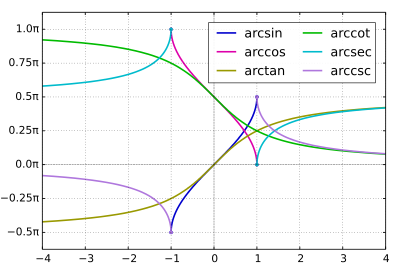
Arkusfunktionen (von lat. arcus „Bogen“), auch zyklometrische Funktionen genannt, sind, wie es ihre alternative Bezeichnung als inverse Winkelfunktionen andeutet, Umkehrfunktionen trigonometrischer Funktionen - die Arkusfunktionen liefern also zu einem gegebenen Winkelfunktionswert den zugehörigen Winkel.
Zu jeder der sechs Winkelfunktionen gibt es eine Arkusfunktion, die in
mathematischen Formeln und Gleichungen durch ein vorangestelltes
oder
vom Kürzel der zugehörigen trigonometrischen Funktion unterschieden wird. Vor
allem im englischsprachigen Raum, aber auch auf den Tastaturen der meisten
Taschenrechner, findet sich immer häufiger eine Schreibweise mit dem
Exponenten −1, der signalisieren soll, dass es sich um die Umkehrfunktion
(aber nicht um den Kehrwert)
der besagten Winkelfunktion handelt:
| Winkelfunktion | Arkusfunktion | Kürzel | alternatives Kürzel |
|---|---|---|---|
| Sinus | Arkussinus | ||
| Kosinus | |||
| Tangens | Arkustangens | ||
| Kotangens | Arkuskotangens | ||
| Sekans | Arkussekans | ||
| Kosekans | Arkuskosekans |
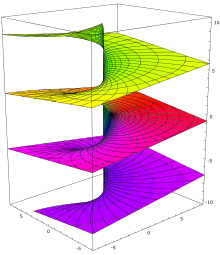
Da die trigonometrischen Funktionen periodische
Funktionen sind, sind sie zunächst einmal nicht invertierbar. Beschränkt
man sich jedoch auf ein Monotonieintervall
der jeweiligen Ausgangsfunktion, z.B. auf das Intervall
oder
,
kann die so erhaltene eingeschränkte Funktion sehr wohl invertiert
werden. Allerdings überdecken die Monotonieintervalle jeweils nur eine halbe
Periode, siehe Abbildung oben. Kennt man jedoch sowohl den Sinus als auch den
Kosinus eines Winkels (allgemeiner: komplexe Komponenten), so kann man den
Winkel bis auf ganze Perioden
ermitteln, siehe Abbildung rechts für die Anschauung und atan2
für die Berechnung.
Beziehungen zwischen den Funktionen
Siehe auch: Trigonometrische Funktion: Beziehungen zwischen den Funktionen
Die Arkusfunktionen lassen sich wie folgt ineinander umrechnen:
| arcsin | arccos | arctan | arccot | arcsec | arccsc | |
|---|---|---|---|---|---|---|
| arcsin(x) | ||||||
| arccos(x) | ||||||
| arctan(x) | ||||||
| arccot(x) | ||||||
| arcsec(x) | ||||||
| arccsc(x) |
Wenn das
verwendet wird, ist zu beachten, dass
für
für
für
für
für
für
Bei der Berechnung von ,
und
müssen die berechneten Werte für
von
abgezogen werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.12. 2019