Arkustangens und Arkuskotangens
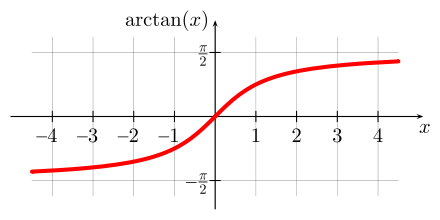

Arkustangens und Arkuskotangens sind zwei miteinander verwandte
mathematische Arkusfunktionen.
Sie sind die Umkehrfunktionen
der geeignet eingeschränkten
Tangens-
und Kotangensfunktionen:
Eine Einschränkung der ursprünglichen Definitionsbereiche
ist nötig, weil Tangens und Kotangens periodische
Funktionen sind. Man wählt beim
Tangens das Intervall
und beim Kotangens das Intervall
.[1]
Zusammen mit Arkussinus und Arkuskosinus als Umkehrfunktionen des Sinus und Kosinus bildet der Arkustangens den Kern der Klasse der Arkusfunktionen. Zusammen mit den Areafunktionen sind sie in der komplexen Funktionentheorie Abwandlungen des komplexen Logarithmus, von dem sie auch die „Mehrdeutigkeit“ erben, die ihrerseits von der Periodizität der komplexen Exponentialfunktion herrührt.
Schreibweisen
Mathematische Formeln verwenden für den Arkustangens als Formelzeichen ,
,
,
oder
.
Für den Arkuskotangens sind die Schreibweisen
und neuerdings auch
in Gebrauch.
Aufgrund der heute für Umkehrfunktionen gebräuchlichen allgemeinen
Schreibweise
beginnt dabei aber auch in diesem Fall die namentlich auf Taschenrechnern
verbreitete Schreibweise
die klassische Schreibweise
zu verdrängen, was leicht zu Verwechslungen mit dem Kehrwert
des Tangens, dem Kotangens,
führen kann (s.a. die Schreibweisen
für die Iteration).
Eigenschaften
| Arkustangens | Arkuskotangens | |
|---|---|---|
| Definitionsbereich | ||
| Bildmenge | ||
| Monotonie | streng monoton steigend | streng monoton fallend |
| Symmetrien | Ungerade Funktion: |
Punktsymmetrie zu |
| Asymptoten | ||
| Nullstellen | keine | |
| Sprungstellen | keine | keine |
| Polstellen | keine | keine |
| Extrema | keine | keine |
| Wendepunkte |
Einige spezielle Werte
| rad | ||||||||
| Grad | ||||||||
Für Tangenswerte
siehe die Formel im Abschnitt Funktionalgleichungen.
Näherungsweise Berechnung
Es gelten folgende Näherungen:
Arkustangens, maximale Abweichung unter 0,005 Radianten:
Arkuskotangens:
Reihenentwicklung
Die Taylorreihe des
Arkustangens mit dem Entwicklungspunkt
lautet:
Die Taylorreihe des Arkuskotangens mit dem Entwicklungspunkt
lautet:
Diese Reihen
konvergieren
genau dann, wenn
und
ist. Zur Berechnung des Arkustangens für
kann man ihn auf einen Arkustangens von Argumenten mit
zurückführen. Dazu kann man entweder die Funktionalgleichung
benutzen oder (um ohne
auszukommen) die Gleichung
Durch mehrfache Anwendung dieser Formel lässt sich der Betrag des Arguments
beliebig verkleinern, was eine sehr effiziente Berechnung durch die Reihe
ermöglicht. Schon nach einmaliger Anwendung obiger Formel hat man ein Argument
mit
sodass obige Taylorreihe konvergiert, und mit jeder weiteren Anwendung wird
mindestens halbiert, was die Konvergenzgeschwindigkeit der Taylorreihe mit jeder
Anwendung der Formel erhöht.
Wegen
hat der Arkuskotangens am Entwicklungspunkt
die Taylorreihe:
Sie konvergiert für
und stimmt dort mit dem oben angegebenen Hauptwert überein. Sie konvergiert auch
für
allerdings mit dem Wert
Manche Pakete der Computeralgebra geben für
den am Ursprung unstetigen,
aber punktsymmetrischen und am unendlich
fernen Punkt stetigen Wert
als Hauptwert.
Funktionalgleichung
Statt aus Argumenten
über 1 oder unter −1 lässt sich der Arkustangens aus Argumenten
zwischen −1 und 1 ableiten:
.
Gleiches gilt für den Arkuskotangens:
.
Wenn man (bspw. durch die erste Ersetzung) bei einem Argument (einem
Tangenswert)
ankommt, kann man anschließend im Fall
die Gleichung
anwenden, sodass mit
das Argument des Arkustangens in jedem Fall (jetzt
,
sonst
)
ins Intervall
mit
zu liegen kommt.
Weitere Beziehungen
Wegen der Punktsymmetrie
ist mit
auch
ein Wertepaar der Arkustangensfunktion.
Summenformeln
Aus dem Additionstheorem für die Tangensfunktion folgt:
Aus dem Additionstheorem für die Kotangensfunktion folgt:
Beispielsweise gilt:
und
Als Arkuskotangens geschrieben:
und
Berechnung der Kreiszahl π mit Hilfe des Arkustangens
Die Reihenentwicklung kann dazu verwendet werden, die Zahl π mit beliebiger Genauigkeit
zu berechnen: Die einfachste Formel ist der Spezialfall
die Leibniz-Formel
Da sie nur extrem langsam (logarithmisch) konvergiert, verwendete John Machin 1706 die Formel
um die ersten 100 Nachkommastellen von
mit Hilfe der Taylorreihe für den Arkustangens zu berechnen. Letztere
konvergiert schneller (linear)
und wird auch heute noch für die Berechnung von
verwendet.
Im Laufe der Zeit wurden noch mehr Formeln dieser Art gefunden. Ein Beispiel stammt von F. C. W. Størmer (1896):
was gleichbedeutend damit ist, dass der Realteil und der Imaginärteil der Gaußschen Zahl
mit
gleich sind.[6]
Gleiches gilt für die Formel von John Machin, wobei es hier um die Gaußsche Zahl
geht, die mit einem Taschenrechner berechnet werden kann.
Ableitungen
Arkustangens:
Arkuskotangens:
Stammfunktionen
Arkustangens:
Eine Stammfunktion des Arkustangens ist
Arkuskotangens:
Eine Stammfunktion des Arkuskotangens ist
Komplexer Arkustangens und Arkuskotangens
Lässt man komplexe Argumente und Werte zu, so hat man
mit
eine Darstellung, die quasi schon in Real- und Imaginärteil aufgespalten ist. Wie im Reellen gilt
mit
Man kann im Komplexen sowohl den Arkustangens (wie auch den Arkuskotangens) durch ein Integral und durch den komplexen Logarithmus ausdrücken:
für
in der zweifach geschlitzten Ebene
Das Integral hat einen Integrationsweg,
der die imaginäre Achse nicht kreuzt außer evtl. im Einheitskreis. Es ist in
diesem Gebiet
regulär und eindeutig.
Der Arkustangens spielt eine wesentliche Rolle bei der symbolischen Integration von Ausdrücken der Form
Ist die Diskriminante
nichtnegativ, so kann man eine Stammfunktion mittels Partialbruchzerlegung
bestimmen. Ist die Diskriminante negativ, so kann man den Ausdruck durch die
Substitution
in die Form
bringen; eine Stammfunktion ist also
Umrechnung ebener kartesischer Koordinaten in polare
Ist ein Punkt
in der Ebene durch Polarkoordinaten
gegeben, so sind seine kartesischen
Koordinaten
durch die Gleichungen
bestimmt.
Die Umrechnung in der Gegenrichtung ist etwas komplizierter. Auf jeden Fall gehört der Abstand
des Punktes
vom Ursprung
zur Lösung. Ist nun
dann ist auch
und es spielt keine Rolle, welchen Wert
hat. Dieser Fall wird im Folgenden als der singuläre Fall bezeichnet.
Ist aber
dann ist
weil die Funktionen
und
die Periode
haben, nur modulo
bestimmt, d.h., mit
ist auch
für jedes
eine Lösung.
Trigonometrische Umkehrfunktionen sind erforderlich, um von Längen zu Winkeln zu kommen. Hier zwei Beispiele, bei denen der Arkustangens zum Einsatz kommt.
Der simple Arkustangens
(s. Abb. 3) reicht allerdings nicht aus. Denn wegen der Periodizität des Tangens
von
muss dessen Definitionsmenge vor der Umkehrung auf eine Periodenlänge von
eingeschränkt werden, was zur Folge hat, dass die Umkehrfunktion (der
Arkustangens) keine größere Bildmenge haben kann.

Halber Winkel
In der nebenstehenden Abb. 3[4]
ist die Polarachse
(die mit der -Achse
definitionsgemäß zusammenfällt) um den Betrag
in die
-Richtung
verlängert, also vom Pol (und Ursprung)
bis zum Punkt
Das Dreieck
ist ein gleichschenkliges,
sodass die Winkel
und
gleich sind. Ihre Summe, also das Doppelte eines von ihnen, ist gleich dem Außenwinkel
des Dreiecks
Dieser Winkel ist der gesuchte Polarwinkel
Mit dem Abszissenpunkt
gilt im rechtwinkligen Dreieck
was nach
aufgelöst
ergibt. Die Gleichung versagt, wenn
ist. Dann muss wegen
auch
sein. Wenn jetzt
ist, dann handelt es sich um den singulären Fall. Ist aber
dann sind die Gleichungen
durch
oder
erfüllt.[5]
Das ist in Einklang mit den Bildmengen
resp.
der Funktion im folgenden Abschnitt.
Der „Arkustangens“ mit zwei Argumenten (atan2)
Ein anderer Weg, um zu einem vollwertigen Polarwinkel zu kommen, ist in
vielen Programmiersprachen
und Tabellenkalkulationen
gewählt worden, und zwar eine erweiterte Funktion, die mit den beiden
kartesischen Koordinaten beschickt wird und die damit genügend Information hat,
um den Polarwinkel modulo
bspw. im Intervall
und in allen vier Quadranten zurückgeben zu können.
Arkustangens mit Lageparameter

In vielen Anwendungsfällen soll die Lösung
der Gleichung
so nahe wie möglich bei einem gegebenen Wert
liegen. Dazu eignet sich die mit dem Parameter
modifizierte Arkustangens-Funktion
Die Funktion
rundet zur engstbenachbarten ganzen Zahl.
Siehe auch
Anmerkungen
- ↑ Beide Funktionen sind monoton in diesen Intervallen, und diese sind von den jeweiligen Polstellen begrenzt.
- ↑
Bspw. sind die Zahlen
Størmer-Zahlen;
dagegen nicht.
- ↑
Dabei ist
- ↑ Eine ganz ähnliche Skizze ist die von Einheitskreis.
- ↑
Beim Rechnen mit Gleitkommazahlen
besteht Instabilität in der Nähe des
-Strahls wegen


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.01. 2022