Wendepunkt

Wendepunkt mit Wendetangente

Krümmungsverhalten der Funktion sin(2x). Die Tangente ist blau gefärbt in konvexen Bereichen, grün gefärbt in konkaven Bereichen und rot gefärbt bei Wendepunkten.

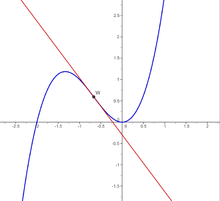
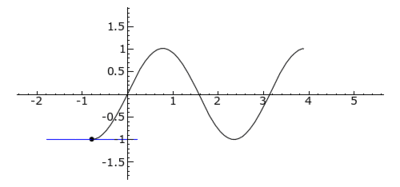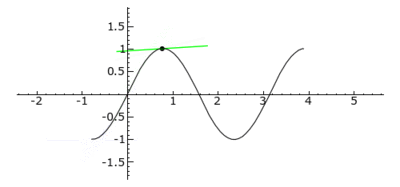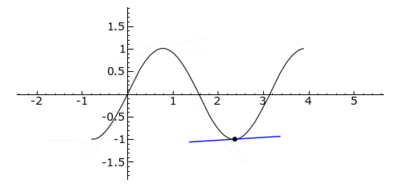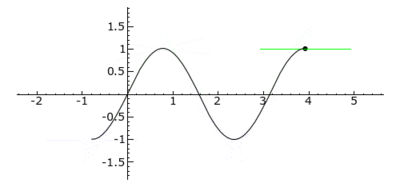
In der Mathematik ist ein Wendepunkt ein Punkt auf einem Funktionsgraphen, an dem der Graph sein Krümmungsverhalten ändert: Der Graph wechselt hier entweder von einer Rechts- in eine Linkskurve oder umgekehrt. Dieser Wechsel wird auch Bogenwechsel genannt. Die Ermittlung von Wendepunkten ist Bestandteil einer Kurvendiskussion.

Ein Wendepunkt $W\left(x_{W}|f(x_{W})\right)$ an der Wendestelle $\ x_{W}$ liegt vor, wenn die Krümmung des Funktionsgraphen an der Stelle $x_{W}$ ihr Vorzeichen wechselt. Daraus lassen sich verschiedene hinreichende Kriterien zur Bestimmung von Wendepunkten ableiten. Ein Kriterium fordert, dass die zweite Ableitung der differenzierbaren Funktion an der Stelle $\ x_{W}$ ihr Vorzeichen wechselt. Andere Kriterien fordern nur, dass die zweite Ableitung der Funktion Null ist und dass bestimmte höhere Ableitungen ungleich Null sind.

Betrachtet man die zweite Ableitung einer Funktion als „Steigung ihrer Steigung“, lassen sich ihre Wendestellen auch als [lokale] Extremstellen, das heißt [lokale] Maxima oder Minima, ihrer Steigung interpretieren.

Tangenten durch einen Wendepunkt (im Bild rot gezeichnet) heißen Wendetangenten. Wendepunkte, in denen diese Wendetangenten horizontal verlaufen, werden Sattel-, Terrassen- oder Horizontalwendepunkte genannt.

Analog zum Begriff Extremwert scheint der Begriff Wendewert für den entsprechenden Funktionswert $f(x_{W})$ intuitiv plausibel und wird auch von manchen Quellen verwendet. Allerdings wird dabei direkt oder indirekt (durch Nutzung von bspw. Anführungszeichen) darauf hingewiesen, dass es sich hierbei um einen tendenziell unüblichen Terminus handelt.

Definition

Sei ${]a,b[}\subset \mathbb{R}$ ein offenes Intervall und $f\colon {]a,b[}\to \mathbb {R}$ eine stetige Funktion. Man sagt, habe in $x_{0}$ einen Wendepunkt, wenn es Intervalle $]\alpha ,x_{0}[$ und $]x_{0},\beta [$ gibt, so dass entweder

in $]\alpha ,x_{0}[$ konvex und in $]x_{0},\beta [$ konkav ist, oder dass
in $]\alpha ,x_{0}[$ konkav und in $]x_{0},\beta [$ konvex ist.

Anschaulich bedeutet dies, dass der Graph der Funktion im Punkt $x_{0}$ das Vorzeichen seiner Krümmung ändert. Die Krümmung einer zweimal stetig differenzierbaren Funktion wird durch ihre zweite Ableitung beschrieben.

Kriterien zur Bestimmung von Wendepunkten

Im Folgenden wird angenommen, dass die Funktion $f\colon {]a,b[}\to \mathbb {R}$ hinreichend oft differenzierbar ist. Gilt dies nicht, so sind die folgenden Kriterien bei der Suche nach Wendepunkten nicht anwendbar. Zuerst wird ein notwendiges Kriterium vorgestellt, das heißt jede zweimal stetig differenzierbare Funktion muss dieses Kriterium an einer Stelle $x_{W}$ erfüllen, damit unter Umständen an diesem Punkt ein Wendepunkt vorliegt. Danach werden einige hinreichende Kriterien angegeben. Sind diese Kriterien erfüllt, so liegt sicher ein Wendepunkt vor, jedoch gibt es auch Wendepunkte, die diese hinreichenden Kriterien nicht erfüllen.

Notwendiges Kriterium

Sei $f\colon {]a,b[}\to \mathbb {R}$ eine zweimal stetig differenzierbare Funktion, dann beschreibt, wie in der Definition schon angemerkt, die zweite Ableitung die Krümmung des Funktionsgraphen. Da ein Wendepunkt ein Punkt ist, an dem sich das Vorzeichen der Krümmung ändert, muss die zweite Ableitung der Funktion an diesem Punkt null sein. Es gilt also:

Ist $x_{W}$ eine Wendestelle, so ist $f\,''(x_{W})=0$ .

Hinreichendes Kriterium ohne Verwendung der dritten Ableitung

Bei Kurvendiskussionen wird in der Regel eine der beiden folgenden hinreichenden Bedingungen verwendet. In der ersten Bedingung kommt nur die zweite Ableitung vor; dafür muss das Vorzeichen von $f\,''(x)$ für $x<x_{W}$ und für $x>x_{W}$ untersucht werden.

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}{\text{ zweimal differenzierbar.}}\\f\,''(x){\text{ wechselt an der Stelle }}x_{W}{\text{ das Vorzeichen.}}\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

Wechselt $\,f''(x_{W})$ vom Negativen ins Positive, so ist $x_{W}$ Rechts-links-Wendestelle. Wenn $\,f''(x_{W})$ an $x_{W}$ vom Positiven ins Negative wechselt, so ist $x_{W}$ eine Links-rechts-Wendestelle.

Hinreichendes Kriterium unter Verwendung der dritten Ableitung

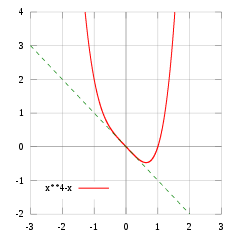
Für die Funktion f(x)=x⁴-x ist die zweite Ableitung bei x=0 gleich Null; aber (0,0) ist kein Wendepunkt, da auch die dritte Ableitung gleich Null und die vierte Ableitung ungleich Null ist.

In der zweiten für einen Wendepunkt hinreichenden Bedingung wird auch die dritte Ableitung benötigt, allerdings nur an der Stelle $x_{W}$ selbst. Diese Bedingung wird vor allem dann verwendet, wenn die dritte Ableitung leicht zu ermitteln ist. Der Hauptnachteil gegenüber der schon erläuterten Bedingung liegt darin, dass im Falle $f\,'''(x_{W})=0$ keine Entscheidung getroffen werden kann.

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}{\text{ dreimal differenzierbar.}}\\f\,''(x_{W})=0\\f\,'''(x_{W})\neq 0\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

Genauer folgt aus $f\,''(x_{W})=0$ und $f\,'''(x_{W})>0$ , dass bei $x_{W}$ ein Minimum des Anstiegs, also eine Rechts-links-Wendestelle besitzt, während sie umgekehrt für $f\,''(x_{W})=0$ und $f\,'''(x_{W})<0$ bei $x_{W}$ ein Maximum des Anstiegs, also eine Links-rechts-Wendestelle aufweist.

Hinreichendes Kriterium unter Verwendung weiterer Ableitungen

Ist die Funktion hinreichend oft differenzierbar, kann auch im Falle $f\,'''(x_{W})=0$ eine Entscheidung getroffen werden. Dies basiert auf der Entwicklung von an der Stelle $x_{0}$ mittels der Taylor-Formel:

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}\,n{\text{-mal differenzierbar.}}\\f\,''(x_{W})=\ldots =f\,^{{(n-1)}}(x_{W})=0\\f\,^{{(n)}}(x_{W})\neq 0\;{\text{ mit }}\,n>2\,{\text{und}}\,n\,{\text{ungerade}}\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

Diese allgemeinere Formulierung enthält damit auch schon den vorangegangenen Fall: Beginnend mit der dritten Ableitung wird die nächste von Null verschiedene Ableitung gesucht, und falls dies eine Ableitung ungerader Ordnung ist, handelt es sich um eine Wendestelle.

Oder ganz allgemein formuliert: Ist die erste von Null verschiedene Ableitung $f^{(n)}$ der Funktion an der Stelle $x_{0}$ , an der $f''(x_{0})=0$ ist, eine Ableitung ungerader Ordnung > 2, besitzt damit an dieser Stelle einen Wendepunkt.

Beispiel

${f(x)}={1 \over 3}\cdot x^{3}-2\cdot x^{2}+3\cdot x$

Dann ist die zweite Ableitung der Funktion gegeben durch:

${f''(x)}={2\cdot x-4}$

Eine Wendestelle $x_{W}$ muss die Bedingung

bzw.

${2\cdot x-4}=0$

erfüllen. Daraus folgt $x_{W}=2$ . Um zu klären, ob an dieser Stelle tatsächlich ein Wendepunkt vorliegt, untersucht man nun auch die dritte Ableitung:

${f'''(x)}=2\,$

Aus $f\,'''(x_{W})=f'''(2)=2\neq 0$ ist zu schließen, dass es sich um einen Wendepunkt handelt. Diese Tatsache ist auch ohne Verwendung der dritten Ableitung zu erkennen: Wegen $f\,''(x)=2\cdot x-4<0$ für x<2 und $f\,''(x)=2\cdot x-4>0$ für x>2 ändert sich das Krümmungsverhalten; daher muss ein Wendepunkt vorliegen.

Die -Koordinate dieses Wendepunkts erhält man durch Einsetzen von x=2 in die Funktionsgleichung.

$y_{W}=f(2)={1 \over 3}\cdot 2^{3}-2\cdot 2^{2}+3\cdot 2={2 \over 3}$

Die Gleichung der Wendetangente kann bestimmt werden, indem man die x-Koordinate des Wendepunktes (2) in die erste Ableitung einsetzt. Somit erhält man die Steigung (m). Danach setzt man in die Funktionsbestimmung (y = mx + b) die ermittelte x- & y-Koordinate des Wendepunkts und den m- (Steigungs-)Wert ein. Man erhält dann den Schnittpunkt mit der y-Achse (b) und somit die komplette Gleichung der Wendetangente.

$f\,'(x)=x^{2}-4\cdot x+3$

$f\,'(2)=2^{2}-4\cdot 2+3=-1$

Wendetangente: $y=-x+{8 \over 3}$

Besondere Fälle

Der Graph der Funktion $f(x)=(x-2)\cdot e^{{|x|}}$ ändert bei x=0 sein Krümmungsverhalten (Übergang von Rechts- in Linkskrümmung). Die erste Ableitung an der Stelle x=0 existiert nicht, der obige Formalismus ist damit nicht anwendbar. Dennoch hat die Funktion bei x=0 einen Wendepunkt.

Der Graph der Funktion mit der Gleichung $f(x)=x^{2}$ im positiven und $f(x)=-x^{2}$ im negativen Bereich und bei x=0 , d.h. f(x)=x|x| , hat zwar eine erste, aber keine zweite Ableitung an der Stelle $0$ , gleichwohl liegt ein Wendepunkt vor.

Basierend auf einem Artikel in:

Wikipedia.de