Exponentialfunktion

In der Mathematik bezeichnet man als Exponentialfunktion eine Funktion der Form $x \mapsto a^x$ mit einer reellen Zahl $a > 0\text{ und } a \neq 1$ als Basis (Grundzahl). In der gebräuchlichsten Form sind dabei für den Exponenten die reellen Zahlen zugelassen. Im Gegensatz zu den Potenzfunktionen, bei denen die Basis die unabhängige Größe (Variable) und der Exponent fest vorgegeben ist, ist bei Exponentialfunktionen der Exponent (auch Hochzahl) des Potenzausdrucks die Variable und die Basis fest vorgegeben. Darauf bezieht sich auch die Namensgebung. Exponentialfunktionen haben in den Naturwissenschaften, z.B. bei der mathematischen Beschreibung von Wachstumsvorgängen, eine herausragende Bedeutung.

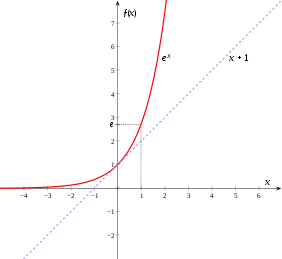
Als natürliche Exponentialfunktion oder e-Funktion bezeichnet man die Exponentialfunktion $x \mapsto e^x$ mit der eulerschen Zahl $e = 2{,}718\,281\,828\,459\dotso$ als Basis; gebräuchlich hierfür ist auch die Schreibweise $x \mapsto \exp(x)$ . Diese Funktion hat gegenüber den anderen Exponentialfunktionen besondere Eigenschaften. Unter Verwendung des natürlichen Logarithmus lässt sich mit der Gleichung $a^{x}=e^{x\cdot \ln a}$ jede Exponentialfunktion auf eine solche zur Basis zurückführen. Deshalb befasst sich dieser Artikel im Wesentlichen mit der Exponentialfunktion zur Basis .

Graph der Exponentialfunktion

(rot) mit der Tangente (hellblau gestrichelte Linie) durch den Punkt 0/1

Definition

Die Exponentialfunktion zu der Basis kann auf den reellen Zahlen auf verschiedene Weisen definiert werden.

Eine Möglichkeit ist die Definition als Potenzreihe, die sogenannte Exponentialreihe

$\exp(x) = \sum_{n = 0}^\infty \frac{x^n}{n!}$ ,

wobei die Fakultät von bezeichnet.

Eine weitere Möglichkeit ist die Definition als Grenzwert einer Folge mit $n\in \mathbb {N}$ :

$\exp(x) = \lim_{n \to \infty} \left( 1 + \frac xn \right)^n$

Beide Arten sind auch zur Definition der komplexen Exponentialfunktion $\exp \colon \mathbb {C} \to \mathbb {C}$ auf den komplexen Zahlen geeignet (s. weiter unten).

Die reelle Exponentialfunktion $\exp\colon\R\to\R_{> 0}$ ist positiv, stetig, streng monoton wachsend und surjektiv. Dabei bezeichnet $\mathbb{R} _{{>0}}$ die Menge der positiven reellen Zahlen.

Sie ist folglich bijektiv. Deshalb existiert ihre Umkehrfunktion, der natürliche Logarithmus $\ln\colon\R_{> 0}\to\R$ .

Daraus erklärt sich auch die Bezeichnung Antilogarithmus für die Exponentialfunktion.

Konvergenz der Reihe, Stetigkeit

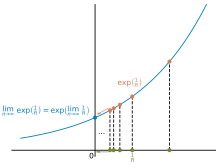
Die Exponentialfunktion ist an der Stelle 0 stetig.

Die punktweise Konvergenz der für die Definition der Exponentialfunktion verwendeten Reihe

IMG class="text" style="width: 49.09ex; height: 6.84ex; vertical-align: -3ex;" alt="\exp(x)=\sum _{{n=0}}^{{\infty }}{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots " src="/svg/f4a1fc022274f96cc01585bb0278719e466ac275.svg">

lässt sich für alle reellen und komplexen $x\;$ einfach mit dem Quotientenkriterium zeigen; daraus folgt sogar absolute Konvergenz. Der Konvergenzradius der Potenzreihe ist also unendlich. Da Potenzreihen an jedem inneren Punkt ihres Konvergenzbereiches analytisch sind, ist die Exponentialfunktion also in jedem reellen und komplexen Punkt trivialerweise auch stetig.

Rechenregeln

Da die Exponentialfunktion die Funktionalgleichung $\exp(x+y)=\exp(x) \cdot \exp(y)$ erfüllt, kann man mit ihrer Hilfe das Potenzieren auf reelle und komplexe Exponenten verallgemeinern, indem man definiert:

$a^{x}:=\exp(x\cdot \ln a)\qquad {\text{bzw.}}\qquad a^{x}:=e^{x\,\cdot \,\ln a}$

für alle a>0 und alle reellen oder komplexen .

Generell gilt diese Umformung von a^x auch für beliebige andere Werte als neue Basis:

$a^x=b^{x\cdot\log_b(a)}$

Solche Funktionen heißen exponentielle Funktionen und „verwandeln“ Multiplikation in Addition. Genauer zeigen das die folgenden Gesetze:

$a^0=1 \,$ und $a^1=a \,$

$a^{x+y}=a^x \cdot a^y$

$a^{{x-y}}={\frac {a^{x}}{a^{y}}}$

$a^{x\cdot y}=(a^{x})^{y}$

$a^{-x} = \frac{1}{a^x}=\left(\frac{1}{a}\right)^x$

$a^x \cdot\ b^x=(a \cdot\ b)^x$

Diese Gesetze gelten für alle positiven reellen $a \,$ und $b \,$ und alle reellen und . Ausdrücke mit Brüchen und Wurzeln können oft mit Hilfe der Exponentialfunktion vereinfacht werden:

$\frac{1}{a}=a^{-1}$

$\sqrt[q]{a^p}=a^\frac{p}{q}$

Siehe auch Rechenregeln für Logarithmus.

Ableitung

Die große Bedeutung der e-Funktion, eben die Exponentialfunktion mit Basis , beruht auf der Tatsache, dass ihre Ableitung wieder die Funktion selbst ergibt:

${\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$

Wenn man zusätzlich

$f(0) = 1 \;$

fordert, ist die e-Funktion sogar die einzige Funktion $f\colon \R\to\R$ , die dies leistet. Somit kann man die e-Funktion auch als Lösung dieser Differentialgleichung f'(x) = f(x) mit dieser Anfangsbedingung f(0) = 1 definieren.

Allgemeiner folgt für reelles a>0 aus

$a^{x}=e^{\left(x\,\cdot \,\ln a\right)}$

und der Kettenregel die Ableitung beliebiger Exponentialfunktionen:

${\frac {\mathrm {d} }{\mathrm {d} x}}a^{b\cdot x}=b\ln a\cdot a^{b\cdot x}$

In dieser Formel kann der natürliche Logarithmus nicht durch einen Logarithmus zu einer anderen Basis ersetzt werden; die Zahl e kommt also in der Differentialrechnung auf „natürliche“ Weise ins Spiel.

Stammfunktion

Aus den Ergebnissen über die Ableitung ergibt sich die Stammfunktion der e-Funktion:

$\int e^{x}\,\mathrm {d} x=e^{x}+C$ .

Für beliebige Exponentialfunktionen mit a>0 und $b\neq 0$ gilt:

$\int a^{b\cdot x}\,\mathrm {d} x={\frac {a^{b\cdot x}}{b\ln a}}+C$ .

Exponentialfunktion auf den komplexen Zahlen

Farbcodierte Darstellung der komplexen Exponentialfunktion. Dunkle Farben bedeuten betragsmäßig kleine Funktionswerte, helle/ausgeblichene Farben bedeuten große Funktionswerte. Die Grundfarbe stellt das Argument des Funktionswerts dar. Dies ist der Winkel, den der Funktionswert relativ zur reellen Achse hat (Blickpunkt im Koordinatenursprung). Positiv reelle Werte erscheinen rot, negativ reelle Werte türkis. Die sich wiederholenden Farbbänder lassen deutlich erkennen, dass die Funktion in imaginärer Richtung periodisch ist.

Realanteil der komplexen Exponentialfunktion

Imaginäranteil der komplexen Exponentialfunktion

Mit Hilfe der Reihendarstellung

$\exp(z) = \sum_{n = 0}^{\infty} \frac{z^n}{n!}$

lässt sich die Exponentialfunktion für komplexe Zahlen definieren. Die Reihe konvergiert für alle $z\in \mathbb {C}$ absolut.

Die Exponentialfunktion behält für alle komplexen Zahlen , folgende wichtige Eigenschaften:

$\exp(z+w)=\exp(z)\cdot \exp(w)$

$\exp(0)=1\,$

$\exp(z) \neq 0$

$\exp '(z)=\exp(z)\,$

Die Exponentialfunktion ist somit ein surjektiver, aber nicht injektiver Gruppenhomomorphismus von der abelschen Gruppe $(\mathbb {C} ,+,0)$ auf die abelsche Gruppe $(\mathbb {C} \setminus \{0\},\cdot ,1)$ , also von der additiven auf die multiplikative Gruppe des Körpers $\mathbb {C}$ .

In $\infty$ hat die Exponentialfunktion eine wesentliche Singularität, ansonsten ist sie holomorph, d.h., sie ist eine ganze Funktion. Die komplexe Exponentialfunktion ist periodisch mit der komplexen Periode $2\pi \mathrm {i}$ , es gilt also

$\exp(z + 2\pi k \mathrm{i}) = \exp(z), \quad k \in \Z.$

Beschränkt man ihren Definitionsbereich auf einen Streifen

$\{z\in \mathbb {C} \,|\,a<\operatorname {Im} (z)<a+2\pi \}$

mit $a\in \mathbb {R}$ , dann besitzt sie eine wohldefinierte Umkehrfunktion, den komplexen Logarithmus.

Die Exponentialfunktion kann zur Definition der trigonometrischen Funktionen für komplexe Zahlen verwendet werden:

$\sin(z) := \frac{e^{\mathrm{i}z} - e^{-\mathrm{i}z}}{2\mathrm{i}},$

$\cos(z) := \frac{e^{\mathrm{i}z} + e^{-\mathrm{i}z}}{2}.$

Dies ist äquivalent zur eulerschen Formel

$e^{\mathrm{i}z} = \cos(z) + \mathrm{i}\,\sin(z)$ .

Daraus abgeleitet ergibt sich speziell die Gleichung

$e^{\mathrm{i} \omega t} =\cos(\omega t) + \mathrm{i}\, \sin(\omega t)$

der in Physik und Technik wichtigen komplexen Exponentialschwingung mit der Kreisfrequenz $\omega =2\pi f$ und der Frequenz .

Ebenso kann die Exponentialfunktion zur Definition der hyperbolischen Funktionen verwendet werden:

$\sinh(z):={\frac {e^{z}-e^{-z}}{2}},$

$\cosh(z):={\frac {e^{z}+e^{-z}}{2}},$

$e^z = \cosh\left(z\right) + \sinh\left(z\right).$

Man kann auch im Komplexen eine allgemeine Potenz definieren:

$z^w = \exp(\ln(z) \cdot w)$ mit $z,\,w \isin \mathbb{C}$ .

Die Werte der Potenzfunktion sind dabei abhängig von der Wahl des Einblättrigkeitsbereichs des Logarithmus, siehe auch Riemannsche Fläche. Dessen Mehrdeutigkeit wird ja durch die Periodizität seiner Umkehrfunktion, eben der Exponentialfunktion, verursacht. Deren grundlegende Gleichung

$\;\mathrm{e}^{2 \pi\,\mathrm{i}} = 1\,$

entspringt der Periodizität der Exponentialfunktion $x \mapsto e^{ix}$ mit reellem Argument . Deren Periodenlänge ist genau der Kreisumfang $2\pi$ des Einheitskreises, den die Sinus- und Kosinusfunktionen wegen der Eulerschen Formel beschreiben. Die Exponential-, die Sinus- und die Kosinusfunktion sind nämlich nur Teile derselben (auf komplexe Zahlen verallgemeinerten) Exponentialfunktion, was im Reellen nicht offensichtlich ist.

Exponentialfunktion auf beliebigen Banachalgebren

Die Exponentialfunktion lässt sich auf Banachalgebren, zum Beispiel Matrix-Algebren mit einer Operatornorm, verallgemeinern. Sie ist dort ebenfalls über die Reihe

$\exp(x) = \sum_{n = 0}^{\infty} \frac{x^n}{n!}$

definiert, die für alle beschränkten Argumente aus der jeweils betrachteten Banachalgebra absolut konvergiert.

Die wesentliche Eigenschaft der reellen (und komplexen) Exponentialfunktion

$\exp(x+y) =\exp(x) \cdot \exp(y)$

ist in dieser Allgemeinheit allerdings nur noch gültig für Werte und , die kommutieren, also für Werte mit $x\cdot y=y\cdot x$ (dies ist in den reellen oder komplexen Zahlen natürlich immer erfüllt, da die Multiplikation dort kommutativ ist). Einige Rechenregeln dieser Art für die Exponentiale von linearen Operatoren auf einem Banachraum liefern die Baker-Campbell-Hausdorff-Formeln.

Eine wichtige Anwendung dieser verallgemeinerten Exponentialfunktion findet sich beim Lösen von linearen Differentialgleichungssystemen der Form $\dot{y}=A\cdot y$ mit konstanten Koeffizienten. In diesem Fall ist die Banachalgebra die Menge der $n\times n$ -Matrizen mit komplexen Einträgen. Mittels der jordanschen Normalform lässt sich eine Basis bzw. Ähnlichkeitstransformation finden, in welcher die Exponentialmatrix eine endliche Berechnungsvorschrift hat. Genauer gesagt, man findet eine reguläre Matrix , so dass $C^{-1}AC=D+N$ , wobei eine Diagonalmatrix und eine nilpotente Matrix sind, welche miteinander kommutieren. Es gilt damit

$\exp(tA)=C\exp(t(D+N))C^{-1}=Ce^{tD}\sum_{k=0}^{n-1}\frac{t^k}{k!}N^k\,C^{-1}$

Das Exponential einer Diagonalmatrix ist die Diagonalmatrix der Exponentiale, das Exponential der nilpotenten Matrix ist ein matrixwertiges Polynom mit einem Grad, der kleiner als die Dimension der Matrix ist.

Siehe auch: Matrixexponential

Numerische Berechnungsmöglichkeiten

Als fundamentale Funktion der Analysis wurde viel über Möglichkeiten zur effizienten Berechnung der Exponentialfunktion bis zu einer gewünschten Genauigkeit nachgedacht. Dabei wird stets die Berechnung auf die Auswertung der Exponentialfunktion in einer kleinen Umgebung der Null reduziert und mit dem Anfang der Potenzreihe gearbeitet. In der Analyse ist die durch die Reduktion notwendige Arbeitsgenauigkeit gegen die Anzahl der notwendigen Multiplikationen von Hochpräzisionsdaten abzuwägen.

Der Rest der -ten Partialsumme hat eine einfache Abschätzung gegen die geometrische Reihe, welche auf

$e^x = \sum_{k=0}^N \frac{x^k}{k!} + \frac{x^{N+1}}{(N+1)!} \, r_N(x)$ bei $\vert r_N(x) \vert < 2$ für alle mit $\vert x \vert < 0{,}5 N+1$ führt.

Die einfachste Reduktion benutzt die Identität $\exp(2z) = \exp(z)^2$ , d.h. zu gegebenem wird $z := 2^{-K} \cdot x$ bestimmt, wobei nach den Genauigkeitsbetrachtungen gewählt wird. Damit wird nun, in einer gewissen Arbeitsgenauigkeit, $y_K \approx e^z$ berechnet und -fach quadriert: $y_{n-1} := y_n^2$ . $y_{0}$ wird nun auf die gewünschte Genauigkeit reduziert und als $\exp(x)$ zurückgegeben.

Effizientere Verfahren setzen voraus, dass $\ln(2)$ , besser zusätzlich $\ln(3)$ und $\ln(5)$ (Arnold Schönhage) in beliebiger (nach Spezifikation auftretender) Arbeitsgenauigkeit verfügbar sind. Dann können die Identitäten

$e^x = 2^k \cdot e^{x-k \cdot \ln(2)}$ oder $e^x = 2^k \cdot 3^l \cdot 5^m e^{x-k \cdot \ln(2)-l \cdot \ln(3)-m \cdot \ln(5)}$

benutzt werden, um auf ein aus dem Intervall $[-0{,}4 \, ;\, 0{,}4]$ oder einem wesentlich kleineren Intervall zu transformieren und damit das aufwändigere Quadrieren zu reduzieren oder ganz zu vermeiden.

Bei Implementierung in Hardware werden für deren Belange geeignete Verfahren genutzt, zum Beispiel:

BKM-Algorithmus
CORDIC

Hintergründe und Beweise

Motivation

Auf die Exponentialfunktion stößt man, wenn man versucht, das Potenzieren auf beliebige reelle Exponenten zu verallgemeinern. Man geht dabei von der Rechenregel $a^{x+y}=a^x a^y$ aus und sucht daher eine Lösung der Funktionalgleichung f(x+y)=f(x)f(y) mit f(1)=a . Nimmt man nun zunächst einmal an, dass eine Lösung tatsächlich existiert, und berechnet deren Ableitung, so stößt man auf den Ausdruck

${\frac {\mathrm {d} }{{\mathrm {d} }x}}a^{x}=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=a^{x}\lim _{h\to 0}{\frac {a^{h}-1}{h}}.$

Was bedeutet nun $\lim_{h\to 0}\frac{a^{h}-1}{h}$ ? Nennt man diesen Grenzwert $\ln a$ , so gilt für die durch

$e:=a^{\frac{1}{\ln a}}$

definierte Zahl (bzw. $a=e^{\ln a}$ , $\ln a$ muss dann also der Logarithmus zur Basis sein) nach der Kettenregel formal

$\frac{\mathrm d}{\mathrm dx}e^x=\frac{\mathrm d}{\mathrm dx}a^{\frac{x}{\ln a}}=a^{\frac{x}{\ln a}}\frac{1}{\ln a}\lim_{h\to 0}\frac{a^{h}-1}{h}=a^{\frac{x}{\ln a}}=e^x.$

erfüllt dann vermutlich

$\lim_{h\to 0}\frac{e^{h}-1}{h}=1.$

Wie kann man diese Zahl berechnen? Setzt man rein formal h=1/n und löst die Gleichung

$\frac{e^{1/n}-1}{1/n}=1$ , dann erhält man $e=\left(1+\frac{1}{n}\right)^n$ . Für die Zahl

$e:=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n$

ist also zu vermuten, dass

$\lim _{{h\to 0}}{\frac {e^{{h}}-1}{h}}=1\qquad {\text{bzw.}}\qquad {\frac {{\mathrm d}}{{\mathrm {d}}x}}e^{x}=e^{x}$

gilt.

Für $e^{x}$ erhält man mit m=nx auch rein formal die Darstellung

$e^x=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^{nx}=\lim_{m\to\infty}\left(1+\frac{x}{m}\right)^m,$

also die eine Definition der Exponentialfunktion.

Taylorreihe

Alternativ kann man auch versuchen, die Funktion

${\frac {{{\mathrm d}}}{{{\mathrm d}}x}}e^{x}=e^{x}$

in eine Taylorreihe zu entwickeln. Da per Induktion auch

${\frac {{\mathrm {d} }^{n}}{{\mathrm {d} }x^{n}}}e^{x}=e^{x}$

gelten muss, also $f^{(n)}(0) = 1$ , erhält man für die Taylorreihe an der Stelle x=0

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots ,$

also genau die andere Definition der Exponentialfunktion. Im Weiteren ist dann zu zeigen, dass die so definierte Exponentialfunktion tatsächlich die gewünschten Eigenschaften hat. Diese Taylorreihe lässt sich auch als Kettenbruch darstellen:

$e^{x}=1+{\cfrac {x}{1-{\cfrac {1x}{2+x-{\cfrac {2x}{3+x-\ddots }}}}}}$

Konvergenz der Folgendarstellung

Die für die Definition der Exponentialfunktion verwendete Folge

$\left(1+{\frac {x}{n}}\right)^{n}$

ist für reelle punktweise konvergent, da sie erstens ab einem gewissen Index monoton steigend und zweitens nach oben beschränkt ist.

Beweis der Monotonie

Aus der Ungleichung vom arithmetischen und geometrischen Mittel folgt für $n\geq-x$

$\begin{align} \sqrt[n+1]{\left(1+\frac{x}{n}\right)^n\cdot 1} &\leq\frac{1}{n+1}\left(n\left(1+\frac{x}{n}\right)+1\right)\\ &=1+\frac{x}{n+1}, \end{align}$

die Folge ist daher für fast alle monoton steigend.

Beweis der Beschränktheit

Aus der Ungleichung vom harmonischen und geometrischen Mittel folgt für n>x

$\begin{align} \sqrt[n+1]{\left(1+\frac{x}{n-x}\right)^n\cdot 1} &=\sqrt[n+1]{\left(\frac{n}{n-x}\right)^n\cdot 1}\\ &\geq \frac{n+1}{1+n\frac{n-x}{n}}\\ &=1+\frac{x}{n+1-x}. \end{align}$

Für $x\geq 0$ und n_0>x ist die Folge daher für alle $n\geq n_0$ beschränkt:

$\left(1+\frac{x}{n}\right)^n \leq \left(1+\frac{x}{n-x}\right)^n\leq \left(1+\frac{x}{n_0-x}\right)^{n_0}.$

Für $x\leq 0$ und $n>\left|x\right|$ gilt offensichtlich die Schranke

$\left(1+\frac{x}{n}\right)^n \leq 1.$

Funktionalgleichung

Da $\left(1+\frac{x}{n}\right)^n$ und $\left(1+\frac{y}{n}\right)^n$ konvergieren, konvergiert auch deren Produkt

$\begin{align} \left(1+\frac{x}{n}\right)^n \left(1+\frac{y}{n}\right)^n &=\left(1+\frac{x+y}{n}+\frac{xy}{n^2}\right)^n\\ &=\left(1+\frac{x+y}{n}\right)^n\left(1+\frac{xy}{n^2+n(x+y)}\right)^n. \end{align}$

Ist nun xy<0 , so liefert die bernoullische Ungleichung für hinreichend große

$1\ge\left(1+\frac{xy}{n^2+n(x+y)}\right)^n\ge 1+\frac{xy}{n+x+y}\to 1$ ;

für xy>0 erhält man aus der einfach zu zeigenden Ungleichung $1+u\le \frac{1}{1-u}$ für u<1 und ebenfalls der bernoullischen Ungleichung für hinreichend große

$\begin{align} 1 & \le\left(1+\frac{xy}{n^2+n(x+y)}\right)^n\\ & \le\frac{1}{\left(1-\frac{xy}{n^2+n(x+y)}\right)^n}\\ & \le\frac{1}{1-\frac{xy}{n+x+y}}\to 1, \end{align}$

die Exponentialfunktion erfüllt also tatsächlich die Funktionalgleichung $\exp(x+y)=\exp(x)\exp(y)$ .

Ungleichungen

Abschätzung nach unten

Für reelle lässt sich die Exponentialfunktion mit

$\exp(x)> 0\;$

nach unten abschätzen. Der Beweis ergibt sich aus der Definition

$\exp(x)=\lim _{{n\to \infty }}\left(1+{\frac {x}{n}}\right)^{n}$

und der Tatsache, dass $1+{\frac {x}{n}}>0$ für hinreichend große . Da die Folge monoton wachsend ist, ist der Grenzwert daher echt größer Null.

Diese Abschätzung lässt sich zur wichtigen Ungleichung

$\exp(x)\geq 1+x$

verschärfen. Für $x\leq-1$ folgt sie aus $\exp(x)\geq 0$ , für $x\geq -1$ ergibt sich der Beweis beispielsweise, indem man die bernoullische Ungleichung auf die Definition

$\exp(x)=\lim _{{n\to \infty }}\left(1+{\frac {x}{n}}\right)^{n}$

anwendet. Eine Anwendung dieser Ungleichung ist der Polya-Beweis der Ungleichung vom arithmetischen und geometrischen Mittel. Allerdings erleichtert die Ungleichung vom arithmetischen und geometrischen Mittel die Untersuchung der Folge $\left(1+{\frac {x}{n}}\right)^{n}$ sehr; um daher einen Zirkelschluss zu vermeiden, benötigt der Polya-Beweis Herleitungen der Exponentialfunktion, die ohne Ungleichung vom arithmetischen und geometrischen Mittel auskommen.

Abschätzung nach oben

Setzt man in der Abschätzung $\exp(x)\geq 1+x$ nach unten statt ein und verwendet $\exp(-x)={\frac {1}{\exp(x)}}$ , so erhält man durch Umstellen der Ungleichung die für alle x < 1 gültige Abschätzung nach oben $\exp(x)\leq {\frac {1}{1-x}}$ .

Ableitung der Exponentialfunktion

Die wichtigste Anwendung dieser beiden Abschätzungen ist die Berechnung der Ableitung der Exponentialfunktion an der Stelle 0:

$\begin{align} 1&=\lim_{h\to 0}\frac{1+h-1}{h}\\ &\le\lim_{h\to 0}\frac{\exp(h)-1}{h}\\ &\le\lim_{h\to 0}\frac{\frac{1}{1-h}-1}{h}\\ &=\lim_{h\to 0}\frac{1}{1-h}\\ &=1. \end{align}$

Gemeinsam mit der Funktionalgleichung $\exp(x+y)=\exp(x)\exp(y)$ folgt daraus die Ableitung der Exponentialfunktion für beliebige reelle Zahlen:

$\begin{align} \exp'(x) &= \lim_{h\to 0}\frac{\exp(x+h)-\exp(x)}{h}\\ & =\exp(x)\lim_{h\to 0}\frac{\exp(h)-1}{h}\\ & =\exp(x). \end{align}$

Wachstum der e-Funktion im Vergleich zu Polynomfunktionen

Oft wird die Aussage benötigt, dass die Exponentialfunktion wesentlich stärker wächst als jede Potenzfunktion, d.h.

$\lim _{x\to \infty }{\frac {x^{r}}{e^{x}}}=0,\quad r\in \mathbb {R}$

Für $r\le0$ ist dies klar, für r>0 kann entweder induktiv die Regel von de l’Hospital benutzt werden, oder auch elegant abgeschätzt werden:

Zunächst gilt

$\frac{x^r}{e^x} = \exp(r\ln x -x).$

Wegen $\ln x < \sqrt{x}$ gilt

$r\ln x -x < r\sqrt{x}-x.$

Dies konvergiert gegen $-\infty$ und somit der obige Grenzwert gegen 0.

Basiswechsel

Wie bereits zuvor erwähnt, gilt

$a^x = b^{x\cdot\log_b(a)}$

Beweis: Nach Definition des Logarithmus ist p = b^y äquivalent zu $y = \log_b(p)$ , woraus die Identität $p = b^{\log_b(p)}$ folgt. Ersetzen von durch a^x liefert

$a^x = b^{\log_b(a^x)} = b^{x \log_b(a)}$

wobei im zweiten Schritt die Logarithmus-Rechenregel für Potenzen angewendet wurde.

Die Differentialgleichung der Exponentialfunktion

Will man die einfache Differentialgleichung: y'=y lösen und setzt noch f(0)=1 voraus, so erhält man daraus eine Definition von $e^{x}$ .

Umkehrfunktion

Setzt man f(0) = 1 nicht voraus, so benutzt man die Umkehrfunktion f(x) von

$\int\limits_{1}^{x}\frac{1}{t} \mathrm{d} t = \ln x = g.$

Denn $x = \log y$ , und nach den Eigenschaften der Logarithmusfunktion ist

$\frac{\mathrm d x}{\mathrm{d} y} = \frac{1}{y},$

und man kann die Umkehrfunktion bilden und erhält

$\frac{\mathrm d y}{\mathrm{d} x} = e^x.$

Da die untere Grenze gleich 1 ist, ist g(1) = 0 und bei der Umkehrfunktion f(0) = 1 nach Eigenschaft der Umkehrfunktion: g(x) = f(y) .

Differentialgleichung

Die Differentialgleichung y = y′ beschreibt den Zusammenhang einer Größe y mit ihrem Wachstum y′ : beide sind gleich groß. Daher wächst y umso schneller, je größer es bereits ist. Die Grafik zeigt exemplarisch vier Lösungen dieser Differentialgleichung, wobei die Exponentialfunktion e^x rot dargestellt ist.

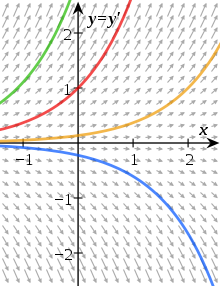
Erweitert man die Differentialgleichung auf $y^\prime = \alpha y$ für y=f(x) und löst sie, so erhält man für die Form

$y = f(x) = ce^{\alpha x}.$

Speziell für $\alpha =1$ ist

Ist dann eine Lösung und $u = ye^{-x}$ , dann ist

$u^\prime = y^\prime e^{-x} - ye^{-x} = e^{-x}(y^\prime - y)$

und nach Voraussetzung

$u^\prime = 0, u = \mathrm{const.} = c\text{ und }y = f(x) = ce^x.$

Für beliebiges $\alpha$ führen wir

$u = ye^{-\alpha x}$

ein. Es ergibt sich

$u^\prime = y^\prime e^{-\alpha x} - \alpha ye^{-\alpha x}$

und nach Voraussetzung wieder

$u^\prime = 0, u = \mathrm{const.} = c\text{ und }y = f(x) = ce^{\alpha x}.$

Man besitzt nun ein Instrument zur Beschreibung von Vorgängen in verschiedenen Bereichen der Wissenschaft, in denen man mittels eines Ansatzes vom Typ $y'=\alpha y$ ein Ergebnis der Form $y = f(x) = ce^{\alpha x}$ erhält, welches auf der Exponentialfunktion basiert.

Beispiele für Exponentialfunktionen

Physik

Als Beispiele für das häufige Auftreten der Exponentialfunktion in der Physik seien genannt:

der radioaktive Zerfall von Teilchen
der Luftdruckverlauf in der Atmosphäre siehe barometrische Höhenformel
zeitliche Ladungskurven eines elektrischen Kondensators
zeitliche Energiekurve beim Einschaltvorgang einer Spule durch Selbstinduktion
Thermodynamik und Statistik: Boltzmann-Faktor, Fermi-Dirac-Statistik, Bose-Einstein-Statistik
die Abkühlung und Erwärmung eines Körpers

Siehe auch: Exponentieller Prozess

Chemie

Als ein Beispiel in der Chemie sei hier eine einfache chemische Reaktion skizziert. Es wird angenommen, dass wir die Lösung eines Stoffes vorliegen haben, etwa Rohrzucker in Wasser. Der Rohrzucker werde nun durch einen Katalysator zu Invertzucker umgewandelt (hydrolysiert). Bei dieser einfachen chemischen Reaktion wird man das Geschwindigkeitsgesetz (unter Vernachlässigung der Rückreaktion) wie folgt formulieren:

Die Reaktionsgeschwindigkeit als Funktion der Zeit ist proportional zur noch vorhandenen Menge der sich umwandelnden Substanz.

Bezeichnen wir die Menge des zur Zeit noch nicht umgewandelten Rohrzuckers mit u(x) , so ist die Reaktionsgeschwindigkeit $-\tfrac{\mathrm d u}{\mathrm d x}$ , und nach dem oben formulierten Geschwindigkeitsgesetz gilt die Gleichung

$\frac{\mathrm d u}{\mathrm d x}=-ku$

mit einer reaktionsspezifischen Geschwindigkeitskonstante . Aus diesem Momentangesetz erhält man nach obiger Differentialgleichung ein Integralgesetz, welches uns die Menge des übriggebliebenen Rohrzuckers als Funktion der Zeit liefert:

$u(x)=ae^{-kx},$

wobei die Konstante die zur Zeit x=0 vorhandene Menge bezeichnet. Die chemische Reaktion nähert sich also asymptotisch ihrem Endzustand u=0 an, der völligen Umwandlung von Rohrzucker in Invertzucker. (Die Vernachlässigung der Rückreaktion ist hier akzeptabel, da das chemische Gleichgewicht der Rohrzucker-Hydrolyse sehr stark auf Seiten des Invertzuckers liegt).

Biologie, Epidemien

Beschreibung des exponentiellen Wachstums in der Anfangszeit einer Population von z.B. Mikroorganismen, Ausbreitung von Infektionen im Rahmen einer Epidemie und Fortpflanzung von Lebewesen, siehe r-Strategie oder SIR-Modell.

Stochastik

Gleiche Anzahl von Münzen und Empfängern

Wie groß sind die Wahrscheinlichkeiten, zufällig keine, eine oder mehr Münzen zu erhalten, wenn Münzen zufällig auf Empfänger verteilt werden und sehr groß ist?

Die Definitionsformel für die Exponentialfunktion

$e^{x}=\lim _{{n\to \infty }}\left(1+{\frac {x}{n}}\right)^{n}$ ,

die daraus abgeleitete Näherungsformel

$e^{x}\approx \left(1+{\frac {x}{n}}\right)^{n}$

und die eulersche Zahl $e=e^{1}$ erlauben eine einfache Abschätzung.

Die Wahrscheinlichkeit, bei der ersten Verteilung eine Münze zu erhalten, beträgt 1/n und 1-1/n , keine Münze zu erhalten. Die Wahrscheinlichkeit, zweimal keine Münze zu erhalten, beträgt: (1-1/n)(1-1/n) . Folglich ist die Wahrscheinlichkeit, -mal erfolglos zu sein:

$P({\text{keine Münze}})=(1-1/n)^{n}\approx 1/e\approx 0{,}37.$

Die Wahrscheinlichkeit, nur einmal Erfolg zu haben, ist das Produkt aus Misserfolgen, Erfolg und der Kombinationsmöglichkeiten , wann sich der Erfolg einstellt (beim ersten Mal, oder zweiten oder dritten …):

$P({\text{eine Münze}})=(1-1/n)^{{n-1}}1/n\cdot n=(1-1/n)^{{n-1}}\approx 1/e\approx 0{,}37.$

Die Wahrscheinlichkeit, mehr als eine Münze zu erhalten, lautet entsprechend:

$P({\text{zwei Münzen und mehr}})=1-P({\text{keine Münze}})-P({\text{eine Münze}})=0{,}26$

Mehr Münzen als Empfänger

Wie viele Münzen müssen es sein, um die Wahrscheinlichkeit P_m , keine zu erhalten, zu verringern, beispielsweise auf 0,1 statt 0,37? Aus obiger Näherungsformel folgt:

$P_m = (1-1/n)^m \leftarrow m = \ln(P_m)/\ln(1-1/n).$

Oder anders gefragt: Wie viele Münzen müssen es mehr sein als Empfänger ?

$m/n = \ln(P_m)/\ln(1-1/n)^n \approx -\ln(P_m).$

Damit im Mittel nur 10 % der Empfänger leer ausgehen, ist die 2,3-fache Menge an Münzen erforderlich, bei 1 % fast die 5-fache Anzahl.

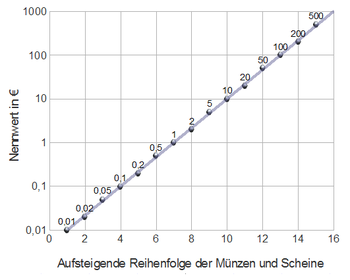
Logarithmische Darstellung des Nominalwerts des Euro

Wirtschaft

Stetige Verzinsung
Die Stückelung folgt üblicherweise einer exponentiellen Gesetzmäßigkeit beim Anstieg des Wertes. Am Beispiel des Euro ist zu den Punkten für jede Münze oder Banknote eine Ausgleichsgerade dargestellt. Die geringen Abweichungen von dieser Geraden folgen aus der Forderung nach „runden“ Zahlen, die mit nur einer signifikanten Stelle exakt anzugeben sind (nicht zu verwechseln mit glatten Zahlen).

Verallgemeinerungen

Wenn $\mathcal A$ eine Größe ist, deren Potenzen $\mathcal A^n$ für beliebiges nicht-negatives ganzzahliges existieren, und wenn der Grenzwert existiert, ist es sinnvoll, die abstrakte Größe $\exp (\mathcal A)$ durch die oben angegebene Exponentialreihe zu definieren. Ähnliches gilt für Operatoren $\mathbf {A}$ , die, einschließlich ihrer Potenzen, eine lineare Abbildung eines Definitionsbereichs $\mathcal D$ eines abstrakten Raumes ${\mathcal {H}}$ (mit Elementen $\psi$ ) in einen Wertebereich $\mathcal W$ der reellen Zahlen ergeben: Hier ist es sogar für alle reellen sinnvoll, in ganz $\mathcal D$ (genauer: im zugehörigen Abschlussbereich) Exponentialoperatoren $\exp (t\cdot \mathbf A)$ durch den Ausdruck $\sum_{n=0}^\infty \,\frac{(t^n\,\mathbf A^n)}{n!}\,\psi$ zu definieren, wobei die Konvergenz dieses Ausdrucks zunächst offenbleibt.

Iteration der Exponentiation führt auf die Verallgemeinerte Exponentialfunktion, die in der Gleitkomma-Arithmetik verwendet wird.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de