Fermi-Dirac-Statistik
Die Fermi-Dirac-Statistik (nach dem italienischen Physiker Enrico Fermi und dem britischen Physiker Paul Dirac) ist ein Begriff der physikalischen Quantenstatistik. Sie beschreibt das makroskopische Verhalten eines Systems, das aus vielen gleichen Teilchen vom Typ Fermion besteht, und gilt z.B. für die Elektronen, die in Metallen und Halbleitern für die elektrische Leitfähigkeit sorgen.
Die Ausgangspunkte der Fermi-Dirac-Statistik sind:
- Keiner der Zustände der einzelnen Teilchen kann mit mehr als einem Teilchen besetzt sein (Pauli-Prinzip).
- Vertauscht man zwei Teilchen miteinander, erhält man keinen neuen Zustand (der in der statistischen Betrachtung extra zu zählen wäre), sondern denselben wie vorher (Prinzip der Ununterscheidbarkeit gleicher Teilchen).
Die Fermi-Verteilung gibt an, mit welcher Wahrscheinlichkeit
in einem idealen
Fermi-Gas bei gegebener absoluter
Temperatur
ein Zustand der Energie
von einem der Teilchen besetzt ist. In der statistischen Physik wird die
Fermi-Verteilung aus der Fermi-Dirac-Statistik für gleichartige Fermionen für den wichtigen
Spezialfall der Wechselwirkungsfreiheit hergeleitet.
Zur vollständigen Beschreibung der Fermi-Dirac-Statistik siehe Quantenstatistik. Für eine vereinfachte Herleitung siehe Ideales Fermigas.
Beschreibung
.png)
zunehmende Abrundung mit steigender Temperatur
(rote Linie: T = 0 K)
Allgemeine Formel
In einem System der Temperatur
lautet die Fermi-Verteilung
,
die die Besetzungswahrscheinlichkeit misst:
mit
- der Energie
für den Zustand eines Teilchens
- dem chemischen
Potential
(Bei
gilt
, wobei
als Fermi-Niveau bezeichnet wird)
- der thermischen
Energie
, die
- die Boltzmann-Konstante
enthält.
- die Boltzmann-Konstante
Wird die Energie
vom tiefstmöglichen Einteilchenzustand aus gerechnet, heißt
auch Fermi-Energie.
Die Besetzungswahrscheinlichkeit W für einen Zustand mit der Energie
des Fermi-Niveaus
ist bei allen Temperaturen:
Um die bei der Energie
herrschende Teilchendichte
zu berechnen, z.B. für Elektronen
in einem Metall, muss die
Fermi-Verteilung noch mit der Zustandsdichte
multipliziert werden:
am absoluten Temperaturnullpunkt
Am absoluten Temperaturnullpunkt
befindet sich das Fermi-Gas als ganzes in seinem energetisch tiefst möglichen
Zustand, also im Grundzustand
des Vielteilchensystems.
Da (bei genügend großer Teilchenzahl) nach dem Pauli-Prinzip
nicht alle Teilchen den Einteilchengrundzustand besetzen können, müssen sich
auch am absoluten Temperaturnullpunkt
Teilchen in angeregten
Einteilchenzuständen befinden. Anschaulich lässt sich das mit der
Vorstellung eines Fermi-Sees beschreiben: jedes hinzugefügte Fermion
besetzt den tiefstmöglichen Energiezustand,
welcher noch nicht von einem anderen Fermion besetzt ist. Die „Füllhöhe“
bestimmt sich aus der Dichte der besetzbaren Zustände und der Anzahl der
unterzubringenden Teilchen.
Entsprechend hat die Fermi-Verteilung für die Temperatur
einen scharfen Sprung bei der Fermi-Energie
,
die daher auch Fermi-Kante oder Fermi-Grenze genannt wird (siehe
Abbildung).
- Alle Zustände
mit
sind besetzt, da hier gilt:
, d.h. die Wahrscheinlichkeit, in einem solchen Zustand eines der Fermionen anzutreffen, ist Eins.
- Keiner der Zustände mit
ist besetzt, da hier gilt:
, d.h. die Wahrscheinlichkeit, in einem solchen Zustand eines der Fermionen anzutreffen, ist Null.
Das Fermi-Niveau bei
ist daher durch die Anzahl und energetische Verteilung der Zustände und die
Anzahl der Fermionen, die in diesen Zuständen unterzubringen sind, festgelegt.
In der Formel erscheint nur eine Energiedifferenz. Gibt man die Größe der
Fermi-Energie allein an, ist es die Energiedifferenz des höchsten besetzten zum
tiefstmöglichen Einteilchenzustand. Zur Veranschaulichung oder zur schnellen
Abschätzung von temperaturabhängigen Effekten wird diese Größe oft als
Temperaturwert – die Fermi-Temperatur – ausgedrückt:
.
Bei der Fermi-Temperatur wäre die thermische Energie
gleich der Fermi-Energie. Dieser Begriff hat nichts mit der realen Temperatur
der Fermionen zu tun, er dient nur der Charakterisierung von
Energieverhältnissen.
bei endlichen Temperaturen
Im Temperaturbereich
bezeichnet man das System als entartetes Fermi-Gas,
denn es wird maßgeblich durch das Ausschließungsprinzip bestimmt, dem zufolge
die Besetzungszahl eines Zustands nicht größer als Eins sein kann. Ausgehend von
werden bei Erwärmung Zustände oberhalb der Fermi-Energie
mit Fermionen besetzt. Dafür bleiben gleich viele Zustände unterhalb der
Fermi-Energie leer und werden als Löcher bezeichnet. Die Fermi-Verteilung
gibt die Besetzungswahrscheinlichkeit im Gleichgewichtszustand zur Temperatur
an.
Im Bereich des entarteten Fermi-Gases, also bei Temperaturen weit unterhalb
der Fermi-Temperatur ,
ist die scharfe Fermi-Kante in einem Bereich der Breite
abgerundet („aufgeweicht“, s. Abb.). Zustände mit kleineren Energien sind
nach wie vor nahezu voll besetzt (
),
die Zustände bei höheren Energien nur sehr schwach (
).
Da nach wie vor die gleiche Teilchenzahl auf die möglichen Zustände zu verteilen ist, kann sich die Fermi-Energie mit der Temperatur verschieben. Ist die Zustandsdichte im Bereich der angeregten Teilchen kleiner als bei den Löchern, muss die Fermi-Energie steigen, im entgegengesetzten Fall sinken.
bei sehr hohen Temperaturen
Bei sehr hohen Energien
und/oder bei sehr hohen Temperaturen (
)
lässt sich die Fermi-Verteilung durch die klassische Boltzmann-Verteilung
nähern:
.
Hier gilt immer .
Das Fermi-Gas verhält sich wie ein klassisches Gas, es ist nicht entartet.
Die Fermi-Energie liegt dann weit unter dem niedrigsten besetzbaren Niveau.
Fermi-Verteilung bei Metallen
Für die Leitungselektronen in einem Metall liegt die Fermi-Energie
bei einigen Elektronenvolt,
entsprechend einer Fermi-Temperatur
von einigen 10.000 K. Dies hat zur Folge, dass die thermische Energie
viel kleiner ist als die typische Breite des Leitungsbands. Es handelt sich um
ein entartetes Elektronengas. Der Beitrag der Elektronen zur Wärmekapazität
ist daher schon bei Raumtemperatur
vernachlässigbar und kann störungstheoretisch
berücksichtigt werden. Die Temperaturabhängigkeit der Fermi-Energie ist sehr
gering (meV-Bereich)
und wird oft vernachlässigt.
Fermi-Verteilung bei Halbleitern und Isolatoren
Für Halbleiter und Isolatoren liegt das
Fermi-Niveau in der verbotenen
Zone. Im Bereich der Fermi-Kante existieren daher keine Zustände,
deren Besetzung deutlich von der Temperatur abhängen kann. Dies führt dazu, dass
bei einer Temperatur
das Valenzband vollständig mit
Elektronen besetzt und das Leitungsband
unbesetzt ist, und dass es bei
nur sehr wenige Löcher bzw. angeregte Elektronen gibt. Durch Einbringen von Fremdatomen
mit zusätzlichen Ladungsträgern
(Donator-
oder Akzeptordotierung) kann das Fermi-Niveau nach unten bzw. nach oben
verschoben werden, was die Leitfähigkeit stark erhöht. In diesem Fall verschiebt
sich auch mit der Temperatur das Fermi-Niveau deutlich. Daher arbeiten
z.B. elektronische Schaltungen auf Basis von Halbleitern (wie im Computer)
nur in einem engen Temperaturbereich richtig.
Herleitung aus einem Minimum der freien Energie
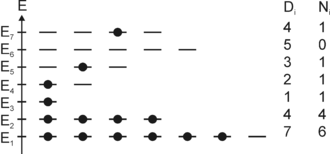
Aus der Bedingung, dass im thermischen Gleichgewicht (bei festem
und Volumen
)
die freie Energie
ein Minimum annimmt, kann die Fermi-Dirac-Statistik auf schöne Art hergeleitet
werden. Dazu betrachten wir
Fermionen – beispielsweise Elektronen –, die über Niveaus
verteilt sind. Die Niveaus haben Energien
und sind jeweils
- fach entartet (s. Abb.), können demnach maximal
Elektronen aufnehmen (Pauli-Prinzip).
Die Anzahl Elektronen im
-ten
Niveau wird mit
bezeichnet. Für den Makrozustand des Systems ist unerheblich, welche der
Elektronen im
-ten
Niveau sind und welche der
Zustände darin sie besetzen. Der Makrozustand wird daher vollständig durch die
Folge der Zahlen
bestimmt.
Für eine beliebige Verteilung der Elektronen auf die Niveaus gilt:
.
Gleichung (1) gibt die Gesamtzahl der Teilchen wieder, die konstant gehalten
werden soll, während die einzelnen
variiert werden, um das Minimum von
zu finden. Gleichung (2) gibt die zur vorliegenden Verteilung gehörende Energie
des Systems an, wie sie in die Formel für
einzusetzen ist. Gleichung (3) ist (nach Ludwig Boltzmann)
die Entropie des Zustands des Systems (Makrozustand),
wobei
die thermodynamische Wahrscheinlichkeit für die betreffende Folge der
Besetzungszahlen
,
angibt, also die Anzahl der möglichen Verteilungen (Mikrozustände) von jeweils
Elektronen auf
Plätze, für alle Niveaus
zusammen.
Um die Verteilung zu finden, bei der durch Variation der
unter der Nebenbedingung
die freie Energie
minimal wird, benutzen wir die Methode der Lagrange-Multiplikatoren.
Es ergibt sich
für alle
.
Darin ist
der (von
unabhängige) Lagrange-Multiplikator. Für die Berechnung der Ableitung
wird die explizite Formel für
benötigt:
Dabei ist
der Binomialkoeffizient, d.h. die Anzahl der Möglichkeiten, unter
Objekten
verschiedene auszuwählen.
Mit Hilfe der vereinfachten Stirlingformel
ergibt sich weiter
und damit
Insgesamt wird Gleichung (2) zu
.
Einsetzen der durch
gegebenen Besetzungswahrscheinlichkeit
und Umstellung ergibt:
.
Dies ist die Fermi-Dirac-Statistik. Der Lagrangemultiplikator erweist sich
als ihr chemisches Potential .
Beobachtungen
In Festkörpern kann die Fermi-Verteilung sehr gut beobachtet werden, wenn die elektronische Besetzungsdichte des Leitungsbandes in Abhängigkeit von der Energie gemessen wird. Ein besonders gutes Beispiel für das ideale Fermigas liegt bei Aluminium vor. Mit solchen Studien lässt sich auch das Auflösungsvermögen einer Messapparatur bestimmen, indem man den Verlauf der Verteilung bei einer bestimmten Temperatur misst und mit der Formel für die Fermi-Verteilung vergleicht.
Weitere Beispiele zur Bedeutung siehe unter Fermi-Energie.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.02. 2022