
Bandlücke
Als Bandlücke (englisch band gap), auch Bandabstand bzw. verbotene Zone, wird der energetische Abstand zwischen Valenzband und Leitungsband eines Festkörpers bezeichnet. Dessen elektrische und optische Eigenschaften werden wesentlich durch die Größe der Bandlücke bestimmt. Die Größe der Bandlücke wird üblicherweise in Elektronenvolt (eV) angegeben.
| Material | Art | Energie in eV | |
|---|---|---|---|
| 0 K | 300 K | ||
| Elemente | |||
| C (als Diamant) | indirekt | 5,4 | 5,46–6,4 |
| Si | indirekt | 1,17 | 1,12 |
| Ge | indirekt | 0,75 | 0,67 |
| Se | direkt | 1,74 | |
| IV-IV-Verbindungen | |||
| SiC 3C | indirekt | 2,36 | |
| SiC 4H | indirekt | 3,28 | |
| SiC 6H | indirekt | 3,03 | |
| III-V-Verbindungen | |||
| InSb | direkt | 0,23 | 0,17 |
| InN | direkt | 0,7 | |
| GaN | direkt | 3,37 | |
| GaP 3C | indirekt | 2,26 | |
| GaAs | direkt | 1,52 | 1,42 |
| AlxGa1-xAs | x < 0,4 direkt, x > 0,4 indirekt |
1,42–2,16 | |
| II-VI-Verbindungen | |||
| TiO2 | 3,03 | 3,2 | |
| ZnO | direkt | 3,436 | 3,37 |
| ZnS | 3,56 | ||
| CdS | 2,42 | ||
| CdSe | 1,74 | ||
| CdTe | 1,45 | ||
Ursprung
Nach dem Bändermodell sind gebundene Zustände der Elektronen nur auf bestimmten Intervallen der Energieskala zugelassen, den Bändern. Zwischen den Bändern können (aber müssen nicht) energetisch verbotene Bereiche liegen. Jeder dieser Bereiche stellt eine Lücke zwischen den Bändern dar, jedoch ist für die physikalischen Eigenschaften eines Festkörpers nur die eventuelle Lücke zwischen dem höchsten noch vollständig mit Elektronen besetzten Band (Valenzband, VBM) und dem nächsthöheren (Leitungsband, CBM) von entscheidender Bedeutung. Daher ist mit der Bandlücke immer diejenige zwischen Valenz- und Leitungsband gemeint.
Das Auftreten einer Bandlücke in manchen Materialien lässt sich quantenmechanisch durch das Verhalten der Elektronen in dem periodischen Potential einer Kristallstruktur verstehen. Dieses Modell der quasifreien Elektronen liefert die theoretische Grundlage für das Bändermodell.
Falls das Valenzband mit dem Leitungsband überlappt, tritt keine Bandlücke auf. Ist das Valenzband nicht vollständig mit Elektronen besetzt, so übernimmt der obere nicht gefüllte Bereich die Funktion des Leitungsbandes, folglich hat man auch hier keine Bandlücke. In diesen Fällen reichen infinitesimale Energiebeträge zur Anregung eines Elektrons aus.
Auswirkungen
Elektrische Leitfähigkeit
Nur angeregte Elektronen im Leitungsband können sich praktisch frei durch einen Festkörper bewegen und tragen zur elektrischen Leitfähigkeit bei. Bei endlichen Temperaturen sind durch thermische Anregung immer einige Elektronen im Leitungsband, jedoch variiert deren Anzahl stark mit der Größe der Bandlücke. Anhand dieser wird deshalb die Klassifizierung nach Leitern, Halbleitern und Isolatoren vorgenommen. Die genauen Grenzen sind unscharf, man kann jedoch in etwa folgende Grenzwerte als Faustregel benutzen:
- Leiter haben keine Bandlücke.
- Halbleiter haben eine Bandlücke im Bereich von 0,1 bis ≈ 4 eV.
- Nichtleiter haben eine Bandlücke größer als 4 eV.
Optische Eigenschaften
Die Fähigkeit eines Festkörpers zur Lichtabsorption
ist an die Bedingung geknüpft, die Photonenenergie
mittels Anregen von Elektronen aufzunehmen. Da keine Elektronen in den
verbotenen Bereich zwischen Valenz- und Leitungsband angeregt werden können,
muss die Energie
eines Photons die Energie
der Bandlücke übertreffen
ansonsten kann das Photon nicht absorbiert werden.
Die Energie eines Photons ist an die Frequenz
(Ny) der elektromagnetischen
Strahlung gekoppelt über die Formel
mit dem Planckschen
Wirkungsquantum
Besitzt ein Festkörper eine Bandlücke, so ist er demnach für Strahlung unterhalb einer gewissen Frequenz / oberhalb einer gewissen Wellenlänge transparent (im Allgemeinen ist diese Aussage nicht ganz korrekt, da es auch andere Möglichkeiten gibt, die Photonenenergie zu absorbieren). Speziell für die Durchlässigkeit von sichtbarem Licht (Photonenenergien um 2 eV) lassen sich folgende Regeln ableiten:
- Metalle können nicht transparent sein.
- Transparente Festkörper sind meistens Isolatoren. Es gibt aber auch elektrisch leitfähige Materialien mit vergleichsweise hohem Transmissionsgrad, z.B. transparente, elektrisch leitfähige Oxide.
Da die Absorption eines Photons mit der Anregung eines Elektrons vom Valenz- ins Leitungsband verbunden ist, besteht ein Zusammenhang mit der elektrischen Leitfähigkeit. Insbesondere sinkt der elektrische Widerstand eines Halbleiters mit steigender Lichtintensität, was z.B. bei Helligkeitssensoren genutzt werden kann, siehe auch unter Fotoleitung.
Arten (mit Bandstrukturdiagramm)
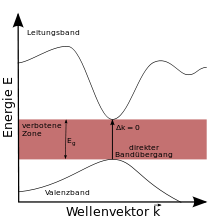
Direkte Bandlücke
Das Minimum des Leitungsbandes liegt im -Diagramm
direkt über dem Maximum des Valenzbandes;
darin ist
der Wellenvektor, der bei
Photonen proportional
ist zu ihrem vektoriellen Impuls:
mit dem reduzierten
Planckschen Wirkungsquantum
Bei einem direkten Übergang vom Valenzband zum Leitungsband liegt der
kleinste Abstand zwischen den Bändern direkt über dem Maximum des Valenzbandes.
Daher ist die Änderung ,
wobei der Impulsübertrag des Photons wegen seiner im Vergleich geringen Größe
vernachlässigt wird.
Anwendungsbeispiele: Leuchtdiode
Indirekte Bandlücke
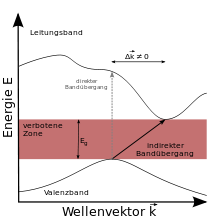
Bei einer indirekten Bandlücke ist das Minimum des Leitungsbandes gegenüber
dem Maximum des Valenzbandes auf der -Achse
verschoben, d.h. der kleinste Abstand zwischen den Bändern ist versetzt.
Die Absorption eines Photons ist nur bei einer direkten Bandlücke effektiv
möglich, bei einer indirekten Bandlücke muss ein zusätzlicher Quasiimpuls (
)
beteiligt werden, wobei ein passendes Phonon
erzeugt oder vernichtet wird. Dieser Prozess mit einem Photon allein ist
aufgrund des niedrigen Impulses des Lichts wesentlich unwahrscheinlicher, das
Material zeigt dort eine schwächere Absorption. Halbleiter, wie Silicium und Germanium, mit einem
indirekten Bandübergang haben daher für die Optoelektronik
ungünstige Eigenschaften.
Einfluss der Kristallstruktur
Wie oben erwähnt ist die Art und Größe der Bandlücke eng mit dem der Kristallstruktur des betrachteten Materials verbunden und nicht auf das chemische Element festgelegt. Daraus folgt, dass andere Kristallisationsformen eines Elements auch andere Eigenschaften der Bandlücke aufweisen können oder dass Verzerrungen der Kristallstruktur (durch äußeren Zwang oder die Temperatur) diese beeinflussen können. So wurde 1973 theoretisch vorhergesagt, dass Germanium (eigentlich ein indirekter Halbleiter in Diamantstruktur) in hexagonaler Kristallstruktur ein direkter Halbleiter ist. 2020 gelang es, hexagonale Silizium-Germanium-Kristalle zu züchten, indem man sie auf Nanodrähte mit Galliumarsenid aufdampfte, die bereits hexagonale Struktur hatten, und somit Silizium-Germanium-Kristalle mit direkter Bandlücke zu erzeugen.
Temperaturabhängigkeit

Die Energie
der Bandlücke nimmt mit steigender Temperatur für viele Materialien zuerst
quadratisch, dann linear ab, und zwar ausgehend von einem maximalen Wert
bei
.
Für einige Materialien, die in Diamantstruktur
kristallisieren, kann die Bandlücke auch mit steigender Temperatur größer
werden. Die Abhängigkeit lässt sich phänomenologisch
u.a. mit der Varshni-Formel beschreiben:
mit der Debye-Temperatur
Die Varshni-Parameter können für unterschiedliche Halbleiter angegeben werden:
| Halbleiter | Eg (T=0K) (eV) |
(10−4 eV/K) |
(K) |
|---|---|---|---|
| Si | 1,170 | 4,73 | 636 |
| Ge | 0,744 | 4,774 | 235 |
| GaAs | 1,515 | 5,405 | 204 |
| GaN | 3,4 | 9,09 | 830 |
| AlN | 6,2 | 17,99 | 1462 |
| InN | 0,7 | 2,45 | 624 |
Dieses Temperaturverhalten ist hauptsächlich auf die relative
Positionsverschiebung von Valenz-
und Leitungsband durch die Temperaturabhängigkeit der Elektron-Phonon Wechselwirkungen zu
erklären. Ein zweiter Effekt, der u.a. bei Diamant zu einem negativen
führt, ist die Verschiebung aufgrund der thermischen Ausdehnung des Gitters.
Diese kann in bestimmten Bereichen nicht-linear und auch negativ werden,
wodurch negative
erklärbar werden.
Anwendungen
Anwendungen gibt es vor allem in der Optik (u.A. verschiedenfarbige Halbleiter-Laser) und in allen Gebieten der Elektrotechnik, wobei man u.A. die Halbleiter- bzw. Isolator-Eigenschaften der Systeme und ihre große Variabilität (z.B. durch Legierung) ausnutzt. Zu den Systemen mit Bandlücke gehören auch die seit etwa 2010 aktuellen sog. topologischen Isolatoren, bei denen zusätzlich zu den Zuständen im Innern, die keinen Strom tragen, (fast) supraleitende Oberflächenströme auftreten.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.01. 2026