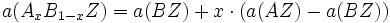III-V-Verbindungshalbleiter

Gruppe	13	15
Periode			Schale
2		7 N	L
3	13 Al	15 P	M
4	31 Ga	33 As	N
5	49 In	51 Sb	O

Hauptgruppe III/V aus dem Periodensystem

Bei einem III-V-Verbindungshalbleiter handelt es sich um eine Verbindung von Materialien der chemischen Hauptgruppe III (Erdmetalle/Borgruppe) und V (Stickstoff-Phosphor-Gruppe), deren Kombination die elektrische Leitfähigkeit von Halbleitern besitzt. III-V-Verbindungshalbleiter sind daher von großer Bedeutung für technische Anwendungen in der Halbleitertechnik.

Mit III-V-Verbindungshalbleitern lässt sich mit Laserdioden bzw. LEDs Licht mit sehr geringer Wellenlänge (UV-Bereich) erzeugen (Anwendungen: weiße Leuchtdiode, BLU-RAY-Disk, HD-DVD.). Umgekehrt eignet sich das Material auch zur Herstellung von Solarzellen mit sehr hohem Wirkungsgrad (über 40 %).

Vertreter

Nitride: Galliumnitrid (GaN), Aluminiumnitrid (AlN), Indiumnitrid (InN)

Die natürliche Kristallisation von Nitriden ist die Wurtzit-Struktur. Mit speziellen Techniken lassen sich auch Zinkblenden-Formationen erzeugen. Zudem existiert auch unter sehr hohem atmosphärischen Druck die chemische Struktur von Steinsalz.

Phosphide: Galliumphosphid (GaP), Aluminiumphosphid (AlP), Indiumphosphid (InP), Indiumgalliumphosphid (InGaP), Borphosphid (BP)
Arsenide: Galliumarsenid (GaAs), Aluminiumarsenid (AlAs), Indiumarsenid (InAs), Borarsenid (BAs)
Antimonide: Galliumantimonid (GaSb), Aluminiumantimonid (AlSb), Indiumantimonid (InSb)

Diese Verbindungen kristallisieren prinzipiell in der Zinkblende-Struktur.

Die binären Materialverbindungen enthalten (bei undotiertem Material) Atome der Gruppe III und V zu gleichen Anteilen. Es können allerdings innerhalb der Gruppen Mischformen erzeugt werden, in denen sich der Anteil an Gruppe-III- bzw. Gruppe-V-Atomen aus zwei Atomsorten zusammensetzt. Dadurch entstehen ternäre (insgesamt drei Atomsorten) und quarternäre (vier Atomsorten) Verbindungen. Beispiele für ternäre Verbindungen sind Aluminiumgalliumarsenid, Indiumgalliumnitrid und Indiumgalliumarsenid. Ein Beispiel für eine quarternäre Verbindung ist 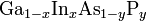$\mathrm{Ga}_{1-x}\mathrm{In}_{x}\mathrm{As}_{1-y}\mathrm{P}_{y}$ .

Herstellung

III-V-Verbindungshalbleiter werden fast ausschließlich durch epitaktisches Wachstum erzeugt. Die Stoffe liegen für die einzelnen Epitaxieverfahren meist gasförmig vor und sind in diesem Zustand bereits in geringen Mengen hochgiftig.

Eigenschaften

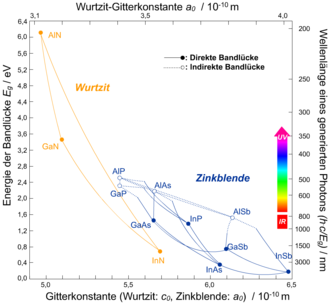
Bandlücke über die Gitterkonstante aufgetragen. Die Linien zwischen den Elementen stellen die ternären Verbindungen dar. Die Wurtzit-Kristallisationen besitzt zwei Gitterkonstanten a und c, die Zinkblende nur eine einzige.

Verbindungshalbleiter aus der Hauptgruppe III und V besitzen den großen Vorteil gegenüber Silizium, dass man ihre Bandlücke mit der Materialzusammensetzung variieren kann. Es lassen sich damit gezielt die elektrischen Eigenschaften verändern. Sie finden damit hauptsächlich technische Anwendungen in optischen Geräten wie Detektoren, Leuchtdioden oder Lasern. Darüber hinaus besitzen einige Verbindungen einen direkten Bandübergang (siehe Bandlücke, Bänderdiagramm), was ihren Einsatz in optischen Anwendungen begünstigt.

Wichtige Materialparameter sind daher zum einen die Bandlückenenergie. Sie bestimmt, welche Wellenlänge des Lichtes (Photonen) bei optischen Anwendungen generiert bzw. absorbiert werden kann. Zum anderen spielt die Gitterkonstante des Materials eine Rolle. Da die Halbleiter nur durch epitaktisches Wachstum hergestellt werden können, müssen die Materialien aufeinander abgestimmt werden. Unterschiede in der Gitterkonstante können einerseits piezoelektrische Ladungen im Material erzeugen, Rekombinationszentren durch dangling bonds bilden, sowie Brüche und Risse provozieren.

Berechnung der ternären Gitterkonstanten

Für die Gitterkonstanten der ternären Mischverbindungen werden zumeist lineare Übergänge angenommen. Dies wird als Vegardsche Regel bezeichnet, und lautet für die Gitterkonstanten a des Mischkristalls A_xB_1-xZ aus den Atomen A, B, Z:

$a(A_xB_{1-x}Z) = a(BZ) + x\cdot \left(a(AZ) - a(BZ)\right)$

Gitterkonstanten (in Å = 10⁻¹⁰m) ausgewählter binäre Verbindungen bei Raumtemperatur
	P	As	Sb	N
	P	As	Sb	a	c
Al	5,4510	5,6605	6,1355	3,112	4,982
Ga	5,4512	5,6533	6,0959	3,189	5,185
In	5,8686	6,0584	6,4794	3,545	5,703

Berechnung der ternären Bandübergangsenergien

Für die Berechnung der Bandübergangsenergien E_g hingegen wird zusätzlich ein quadratischer Term verwendet. Mit diesem Term werden die experimentell ermittelten Werte bestmöglich an eine gebogene Kurve angenähert. Die konstanten Zusatzterme dafür heißen Beugungsparameter 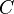(engl.: bowing parameter).

$E_{{\mathrm {g}}}(A_{x}B_{{1-x}}Z)=x\cdot E_{{\mathrm {g}}}(AZ)+(1-x)\cdot E_{{\mathrm {g}}}(BZ)+x\cdot (1-x)\cdot C(A_{x}B_{{1-x}}Z)$

Siehe auch

II-VI-Verbindungshalbleiter

Basierend auf einem Artikel in:

Wikipedia.de