Impuls

Name

Impuls

${\vec {p}}$

Größen- und Einheitensystem	Einheit	Dimension
SI	N·s kg·m·s⁻¹	M·L·T⁻¹

Der Impuls ist eine grundlegende physikalische Größe, die den mechanischen Bewegungszustand eines physikalischen Objekts charakterisiert. Der Impuls eines physikalischen Objekts ist umso größer, je schneller es sich bewegt und je massereicher es ist. Damit steht der Impuls für das, was in der Umgangssprache unscharf mit „Schwung“ und „Wucht“ bezeichnet wird.

Das Formelzeichen des Impulses ist meist (von lateinisch pellere ‚stoßen, treiben‘). Die Einheit ist im Internationalen Einheitensystem kg·m·s⁻¹ = N·s.

Im Gegensatz zur kinetischen Energie ist der Impuls eine vektorielle Größe und hat damit einen Betrag und eine Richtung. Seine Richtung ist die Bewegungsrichtung des Objekts. Sein Betrag ist in der klassischen Mechanik durch das Produkt aus der Masse des Körpers und der Geschwindigkeit seines Massenmittelpunkts gegeben. In der relativistischen Mechanik gilt eine andere Formel (Viererimpuls), die für Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit näherungsweise mit der klassischen Formel übereinstimmt. Sie schreibt aber auch masselosen Objekten, die sich mit Lichtgeschwindigkeit bewegen, einen Impuls zu, z.B. klassischen elektromagnetischen Wellen oder Photonen.

Der Impuls eines Körpers charakterisiert ausschließlich die Translationsbewegung seines Massenmittelpunkts. Eine eventuell zusätzlich vorhandene Rotation um den Massenmittelpunkt wird durch den Drehimpuls beschrieben. Der Impuls ist eine additive Größe. Der Gesamtimpuls eines Objekts mit mehreren Bestandteilen ist die Vektorsumme der Impulse seiner Teile.

Der Impuls hängt, wie die Geschwindigkeit und die kinetische Energie, von der Wahl des Bezugssystems ab. In einem fest gewählten Inertialsystem ist der Impuls eine Erhaltungsgröße, das heißt: Ein Objekt, auf das von außen keine Kräfte wirken, behält seinen Gesamtimpuls nach Betrag und Richtung bei. Üben zwei Objekte Kraft aufeinander aus, z.B. bei einem Stoßvorgang, ändern sich ihre beiden Impulse in entgegengesetzter Weise so, dass ihre vektorielle Summe erhalten bleibt. Die Größe, um die sich der Impuls für eines der Objekte ändert, wird als Impulsübertrag bezeichnet. Im Rahmen der klassischen Mechanik ist der Impulsübertrag unabhängig von der Wahl des Inertialsystems.

Der Impulsbegriff entwickelte sich aus der Suche nach dem Maß für die in einem physikalischen Objekt vorhandene „Menge an Bewegung“, die aller Erfahrung nach bei allen inneren Prozessen erhalten bleibt. Daraus erklären sich die heute veralteten Bezeichnungen „Bewegungsgröße“ oder „Bewegungsmenge“ für den Impuls. Mit diesen Bezeichnungen konnte ursprünglich auch die kinetische Energie gemeint sein; erst Anfang des 19. Jahrhunderts wurden die Begriffe sauber unterschieden. Im Englischen wird der Impuls momentum genannt, während impulse den Impulsübertrag (Kraftstoß) bezeichnet.

Definition, Zusammenhänge mit Masse und Energie

Klassische Mechanik

Der Impulsbegriff wurde von Isaac Newton eingeführt: Er schreibt in Principia Mathematica>:

„Quantitas motus est mensura ejusdem orta ex velocitate et quantitate materiae conjunctim.“

„Die Größe der Bewegung wird durch die Geschwindigkeit und die Größe der Materie vereint gemessen.“

Mit „Größe der Materie“ ist die Masse gemeint, mit „Größe der Bewegung“ der Impuls. In heutiger Formelsprache ausgedrückt lautet diese Definition also:

${\vec p}=m\cdot {\vec v}$

Da die Masse eine skalare Größe ist, sind Impuls ${\vec {p}}$ und Geschwindigkeit ${\vec {v}}$ Vektoren mit gleicher Richtung. Ihre Beträge lassen sich nicht miteinander vergleichen, denn sie haben verschiedene physikalische Dimensionen.

Um die Geschwindigkeit eines Körpers (nach Richtung und/oder Betrag) zu ändern, muss sein Impuls geändert werden. Der übertragene Impuls dividiert durch die dafür benötigte Zeit ist die Kraft ${\vec {F}}$ :

${\frac {\mathrm {d} {\vec {p}}}{\mathrm {d} t}}={\vec {F}}$

Aus dem Zusammenhang zwischen dem Impuls eines Körpers und der auf ihn gewirkten Kraft resultiert für die verrichtete Beschleunigungsarbeit auch ein Zusammenhang zum Impuls:

$W=\int \limits _{C}{\vec {F}}({\vec {s}})\cdot \mathrm {d} {\vec {s}}=\int \limits _{C}{\vec {F}}({\vec {s}})\,\mathrm {d} t\cdot {\frac {\mathrm {d} {\vec {s}}}{\mathrm {d} t}}=\int \limits _{C}\mathrm {d} {\vec {p}}\cdot {\vec {v}}={\frac {1}{m}}\int \limits _{C}\mathrm {d} {\vec {p}}\cdot {\vec {p}}$

Diese Beschleunigungsarbeit ist die kinetische Energie. Es folgt

$E_{\text{kinetisch}}={\frac {{\vec {p}}^{\,2}}{2\,m}}={\frac {m\;{\vec {v}}^{\,2}}{2}}$ .

Spezielle Relativitätstheorie

Nach der Relativitätstheorie ist der Impuls eines mit der Geschwindigkeit bewegten Körpers mit Masse m>0 durch

${\vec p}={\frac {m\cdot {\vec v}}{{\sqrt {1-{v^{2} \over c^{2}}}}}}$

gegeben. Darin ist die Lichtgeschwindigkeit und stets v<c . Der Impuls hängt von der Geschwindigkeit nichtlinear ab, er steigt bei Annäherung an die Lichtgeschwindigkeit gegen Unendlich.

Allgemeingültig ist die Energie-Impuls-Beziehung

$E^{2}-p^{2}\cdot c^{2}=m^{2}\cdot c^{4}.$

Für Objekte mit Masse folgt:

$E = \frac{m \cdot c^2}{\sqrt{1-{v^2 \over c^2}}}$

Für v=0 folgt p=0 und $E=m\,c^{2}$ (Ruheenergie).

Objekte ohne Masse bewegen sich stets mit Lichtgeschwindigkeit. Für diese folgt aus der Energie-Impuls-Beziehung

$E=p\,c$

und damit ergibt sich für sie der Impuls

$p={E \over c}.$

Elektromagnetisches Feld

Siehe auch: Energie-Impuls-Tensor

Ein elektromagnetisches Feld mit elektrischer Feldstärke ${\vec {E}}$ und magnetischer Feldstärke ${\vec {H}}$ hat die Energiedichte

$u={\frac {1}{2}}\varepsilon _{0}E^{2}+{\frac {1}{2}}\mu _{0}H^{2}.$

Dazu gehören die Energiestromdichte (Poynting-Vektor)

${\vec {S}}={\vec {E}}\times {\vec {H}}$

und die Impulsdichte

$\qquad {\vec {g}}={\frac {1}{c^{2}}}{\vec {E}}\times {\vec {H}}.$

Über ein bestimmtes Volumen integriert ergeben diese drei Ausdrücke die Energie , den Energiestrom und den Impuls , die mit dem gesamten in diesem Volumen befindlichen Feld verbunden sind. Für fortschreitende ebene Wellen ergibt sich wieder $E=p\,c$ .

Impulserhaltung

Anstoß beim Poolbillard: Der Impuls der weißen Kugel verteilt sich auf alle Kugeln.

→ Hauptartikel: Impulserhaltungssatz

In einem Inertialsystem ist der Impuls eine Erhaltungsgröße. In einem physikalischen System, auf das keine äußeren Kräfte wirken, (in diesem Zusammenhang auch als abgeschlossenes System bezeichnet), bleibt die Summe aller Impulse der zum System gehörenden Bestandteile konstant.

Der anfängliche Gesamtimpuls ist dann also auch gleich der Vektorsumme der zu irgendeinem späteren Zeitpunkt vorhandenen Einzelimpulse. Stöße und andere Vorgänge innerhalb des Systems, bei denen sich die Geschwindigkeiten der Bestandteile ändern, enden stets so, dass dieses Prinzip nicht verletzt wird (siehe Kinematik (Teilchenprozesse)).

Die Impulserhaltung gilt auch beim unelastischen Stoß. Dabei nimmt durch plastische Verformung oder andere Prozesse die kinetische Energie zwar ab, aber der Impulserhaltungssatz ist vom Energieerhaltungssatz unabhängig und gilt sowohl bei elastischen als auch bei unelastischen Stößen.

Kraftstoß

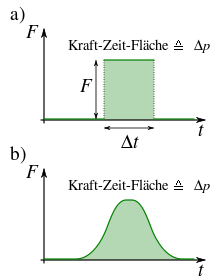
Impulsänderung und Kraft-Zeit-Fläche

Aus der Kraft auf einen Körper und deren Einwirkungsdauer ergibt sich eine Impulsänderung, die als Kraftstoß bezeichnet wird. Dabei spielen sowohl der Betrag als auch die Richtung der Kraft eine Rolle. Der Kraftstoß wird oft mit dem Formelzeichen ${\vec {I}}$ bezeichnet, seine SI-Einheit ist 1 N·s.

Ist die Kraft ${\vec {F}}$ im Zeitintervall $\Delta t_{{1,2}}:=t_{2}-t_{1}$ (mit $t_{1}<t_{2}$ ) konstant, so kann der Kraftstoß berechnet werden als:

${\vec I}(t_{1},t_{2})=\Delta {\vec p}={\vec F}\cdot \Delta t_{{1,2}}$

Ist ${\vec {F}}$ dagegen nicht konstant, aber dennoch ohne Vorzeichenwechsel (in jeder einzelnen Kraftkomponente), so kann man unter Ausnutzung des Mittelwertsatzes der Integralrechnung mit einer mittleren Kraft rechnen.

Im allgemeinen Fall ist ${\vec {F}}$ zeitabhängig und der Kraftstoß durch Integration definiert:

${\vec {I}}(t_{1},t_{2})=\Delta {\vec {p}}(t_{1},t_{2})=\int _{t_{1}}^{t_{2}}{\vec {F}}(t)\cdot \mathrm {d} t$

Impuls im Lagrange- und Hamilton-Formalismus

Im Lagrange- und Hamilton-Formalismus wird der generalisierte Impuls eingeführt; die drei Komponenten des Impulsvektors zählen zum generalisierten Impuls; aber auch beispielsweise der Drehimpuls.

Im Hamilton-Formalismus und in der Quantenmechanik ist der Impuls die zum Ort kanonisch konjugierte Variable. Der (generalisierte) Impuls wird in diesem Zusammenhang auch als kanonischer Impuls bezeichnet. Die möglichen Paare (q,p) von generalisierten Ortskoordinaten > und kanonischen Impulsen eines physikalischen Systems bilden in der hamiltonschen Mechanik den Phasenraum.

In Magnetfeldern enthält der kanonische Impuls eines geladenen Teilchens einen zusätzlichen Term, der mit dem Vektorpotential des B-Felds in Zusammenhang steht (siehe Generalisierter Impuls).

Impuls in strömenden Medien

Bei kontinuierlich verteilter Masse, wie beispielsweise in der Strömungsmechanik, enthält ein kleines Gebiet um den Punkt ${\vec {x}}$ die Masse $\rho (t,{\vec {x}})\,\mathrm {d} ^{3}x.$ Dabei ist $\mathrm d^3 x$ das Volumen des Gebietes. $\rho(t,\vec{x})$ ist die Massendichte und ${\vec {x}}=(x_{1},x_{2},x_{3})$ der Ortsvektor (Komponenten nummeriert). Sie kann sich mit der Zeit ändern.

Wenn diese Masse sich mit der Geschwindigkeit ${\vec {v}}(t,{\vec {x}})$ bewegt, hat sie den Impuls $\rho(t,\vec{x})\,\vec{v}(t,\vec{x})\,\mathrm d^3 x$ . Dividiert durch das Volumen ergibt sich die Impulsdichte als Massendichte mal Geschwindigkeit: $\rho \,{\vec {v}}$ >.

Wegen der Impulserhaltung gilt für die Impulsdichte an einem festen Ort die Kontinuitätsgleichung

${\frac {\partial (\rho \,{\vec {v}})}{\partial t}}={\vec {f}}-\sum _{i=1}^{3}{\frac {\partial }{\partial x_{i}}}(\rho \,{\vec {v}}\,v_{i}),$

die besagt, dass sich die zeitliche Änderung der Impulsdichte zusammensetzt aus der auf das Volumenelement wirkende Kraftdichte (zum Beispiel der Gradient des Drucks oder das Gewicht, ${\vec {f}}_{\text{Gravitation}}=\rho \,{\vec {g}}$ ) und dem Impulsstrom in das Gebiet hinein und heraus.

Die Eulerschen Gleichungen sind das System von partiellen Differentialgleichungen, das zusammen mit Impulserhaltung und Energieerhaltung die Zeitentwicklung eines kontinuierlichen Systems zulässt. Die Navier-Stokes-Gleichungen erweitern diese Gleichungen, indem sie zusätzlich Viskosität beschreiben.

Bemerkenswert an der Eulerschen Gleichung ist, dass es für den Impuls eine Erhaltungsgleichung gibt, für die Geschwindigkeit aber nicht. In der klassischen Mechanik spielt das keine besondere Rolle, da es den einfachen skalaren Zusammenhang ${\vec {p}}=m{\vec {v}}$ gibt. In den relativistischen Eulergleichungen hingegen mischt in jede Vektorkomponente der Lorentzfaktor, der von ${\vec {v}}^{2}$ abhängt. Deswegen ist die Rekonstruktion des Geschwindigkeitsvektors (primitive Variablen) aus dem System von relativistischer Masse, Impuls und Energiedichte (konservierte Variablen) in der Regel mit der Lösung eines nichtlinearen Gleichungssystems verbunden.

Impuls in der Quantenmechanik

In der Quantenmechanik spielt der Impuls eine entscheidende Rolle. Für Impuls- und Ortsbestimmung gilt die heisenbergsche Unschärferelation, nach der ein Teilchen nicht zugleich einen genauen Impuls und einen genauen Ort haben kann. Der Welle-Teilchen-Dualismus erfordert, bei quantenmechanischen Objekten gleichzeitig ihre Wellen- und Teilchennatur in Betracht zu ziehen. Während ein wohldefinierter Ort, aber ein wenig definierter Impuls intuitiv besser zum Teilchenverständnis passt, ist ein wohldefinierter Impuls (der Wellenvektor) eher eine Eigenschaft der Welle. Die Dualität bildet sich mathematisch darin ab, dass man die kanonische Quantenmechanik entweder im Ortsraum oder Impulsraum betreiben kann (auch Ortsdarstellung und Impulsdarstellung genannt). Je nach Darstellung ist der Impulsoperator dann ein gewöhnlicher Messoperator, oder es handelt sich um einen Differentialoperator. In beiden Fällen sorgt die Messung des Impulses dafür, dass er anschließend exakt bestimmt ist; es findet ein Kollaps der Wellenfunktion statt, der zur totalen Delokalisierung des Objektes führt. Umgangssprachlich wird dies manchmal dadurch ausgedrückt, dass „zu einem physikalischen Zustand eines Teilchens kein bestimmter Impuls gehört“ oder „nur die Wahrscheinlichkeit angegeben werden kann, dass der Impuls eines Teilchens in diesem oder jenem Bereich liegt“. Diese Aussagen sind allerdings durch ein teilchen- bzw. ortszentriertes Denken geprägt und lassen sich ebenso umdrehen: „Zu einem physikalischen Zustand einer Welle gehört kein bestimmter Ort“ oder „es kann nur die Wahrscheinlichkeit dafür angegeben werden, dass der Ort einer Welle in diesem oder jenem Bereich liegt“.

Die Zustände mit wohlbestimmtem Impuls heißen Eigenzustände des Impulsoperators. Ihre Wellenfunktionen sind ebene Wellen mit der Wellenlänge

$\lambda ={\frac {h}{p}},$

wobei das plancksche Wirkungsquantum ist und der Impuls. Die De-Broglie-Wellenlänge $\lambda$ von Materiewellen freier Teilchen ist also durch den Impuls bestimmt.

Literatur

Dieter Meschede: Gerthsen Physik. 24., überarbeitete Auflage. Springer, Heidelberg / Dordrecht / London / New York 2010, ISBN 978-3-642-12893-6.
Florian Scheck: Theoretische Physik 1. 8. Auflage. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-71377-7.

Basierend auf einem Artikel in:

Wikipedia.de