
Magnetische Flussdichte
| Physikalische Größe | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Magnetische Flussdichte | |||||||||||||||
| Formelzeichen | ||||||||||||||||
| ||||||||||||||||
Die magnetische Flussdichte, auch magnetische Induktion, bisweilen in der fachlichen Umgangssprache einfach nur „Flussdichte“ oder „Magnetfeld“ oder „B-Feld“ genannt, ist eine physikalische Größe der Elektrodynamik. Sie ist die Flächendichte des magnetischen Flusses, der senkrecht durch ein bestimmtes Flächenelement hindurchtritt.
Die magnetische Flussdichte
an einem Ort
ist – ebenso wie die elektrische
Flussdichte
– eine gerichtete Größe, also ein Vektor,
und wird aus dem Vektorpotential
hergeleitet.
Definition und Berechnung
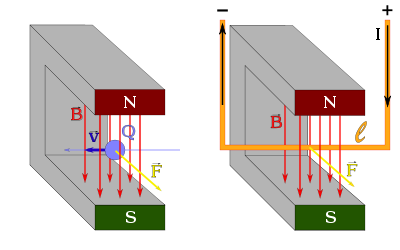
Wie die elektrische
Feldstärke
ist auch die magnetische Flussdichte
historisch zunächst einmal indirekt, d.h. über ihre experimentell messbare
Kraftwirkung
auf bewegte elektrische Ladungen, definiert worden, die in der neueren
Physik als magnetische Komponente der Lorentzkraft
betrachtet und in vektorieller Schreibweise wie folgt notiert wird:
mit:
– bewegungsbedingte Kraftwirkung auf die Ladung
im Magnetfeld
– elektrische Ladung, oder
- Stromstärke
– Geschwindigkeit der Ladungsbewegung, oder
– Länge des Wegs des elektrischen Stroms
durch den untersuchten Leiter (Die Orientierung von
richtet sich nach der technischen Stromrichtung)
– magnetische Flussdichte
Die erste der beiden oben aufgeführten Gleichungen wird vorwiegend für frei im Raum bewegliche Ladungen, z.B. Elektronen innerhalb einer Braunschen Röhre, benutzt, die zweite dagegen für Ladungen, die sich innerhalb von elektrischen Leitern, z.B. Drähten oder Kabeln, bewegen. Beide Gleichungen sind gleichwertig.
In den genannten Formeln ist
ein Vektor, der in Richtung der Feldlinien des erzeugenden Magnetfelds zeigt.
Verzichtet man auf die vektorielle Schreibweise und damit die Möglichkeit,
die Richtung der Kraftwirkung
aus dem Vektorprodukt
der beiden Vektoren
und
bzw.
und
zu bestimmen, kann
gemäß folgender Formel auch als skalare
Größe berechnet werden:
mit:
– elektrische Ladung, oder
– Stromstärke
– Geschwindigkeit der Ladungsbewegung, oder
– Länge des Wegs des Stroms im Leiter
– Betrag der magnetischen Flussdichte
– Winkel zwischen der Richtung der Ladungsbewegung und der Richtung des magnetischen Flusses, oder zwischen der Richtung des Stromflusses
und der Richtung des magnetischen Flusses.
Bewegt sich die elektrische Ladung
mit der Geschwindigkeit
senkrecht zur Richtung des magnetischen Flusses und/oder verläuft der
untersuchte elektrische Leiter senkrecht zur magnetischen Flussrichtung, kann,
da
in diesem Fall den Wert 1 annimmt, der Zahlenwert von
gemäß folgender Gleichung auch direkt aus der Kraftwirkung
auf die Ladung bzw. den Leiter als ganzes berechnet werden:
Der Zusammenhang mit der magnetischen Feldstärke
ist:
.
Dabei ist
die magnetische
Permeabilität.
Messung
Die magnetische Flussdichte kann mit Magnetometern, Hallsensoren oder Messspulen gemessen werden.
Maßeinheit
Die SI-Einheit der magnetischen Flussdichte ist das Tesla mit dem Einheitenzeichen T:
Eine veraltete Einheit für die magnetische Flussdichte ist außerdem das Gauß mit dem Einheitenzeichen G, das allerdings in der Technik immer noch verwendet wird. Es gilt 1 T = 10000 G.
Spezialfälle
Im Folgenden werden der Einfachheit halber nur die Beträge der Flussdichten angegeben.
- magnetische Flussdichte im Abstand
von einem geraden stromdurchflossenen Leiter:
-
- (Die Richtung der Flussdichte ergibt sich aus der Korkenzieherregel.)
- im Inneren einer langen Spule:
-
- (Hierbei sind
die Windungszahl und
die Länge der Spule. Streng genommen ist dies nur eine Näherungsformel, die nur unter folgenden Voraussetzungen gilt: Die Länge der Spule ist groß verglichen mit dem Radius der Spule, die Windungen sind sehr dicht und gleichmäßig und der betrachtete Ort befindet sich im Inneren der Spule und nicht in der Nähe der Spulenenden. Die Richtung der Flussdichte verläuft parallel zur Spulenachse. Für die Orientierung siehe dort. Außerhalb der Spule ist die Flussdichte nahezu Null.)
- in der Mitte einer Helmholtz-Spule
mit Radius
:
- in einiger Entfernung
von einem magnetischen Dipol mit dem Dipolmoment
:
-
- (Das Dipolmoment einer kreisförmigen Leiterschleife mit der orientierten
Querschnittsfläche
ist
.)
Magnetische Flussdichte und magnetischer Fluss
Die magnetische Flussdichte
ist als Flächendichte über folgende Beziehung mit dem magnetischen Fluss
verknüpft:
Dass die Flusslinien des magnetischen Flusses in sich geschlossen sind, lässt
sich mathematisch dadurch zum Ausdruck bringen, dass jedes Flächenintegral
von
über eine beliebige geschlossene Oberfläche
den Wert 0 annimmt:
Diese Gleichung ist mathematisch gesehen eine direkte Konsequenz der homogenen Maxwellschen Gleichung
sowie des Gaußschen Satzes
für ein beliebiges Vektorfeld
und das von
eingeschlossene Volumen
.
Anschaulich gesprochen: Wenn man sich ein durch eine beliebig geformte
geschlossene Fläche
eingeschlossenes Volumen
in einem magnetischen Feld vorstellt, fließt stets genauso viel „Magnetismus“
aus
durch die Oberfläche
nach außen wie von außen hinein. Dies bezeichnet man als „Quellenfreiheit des
magnetischen Feldes“.
Größenbeispiele
Beispiele für verschiedene magnetische Flussdichten in der Natur und in der Technik:
| Magnetische Flussdichte |
Beispiel |
|---|---|
| 0,1 bis 10 nT | Magnetfelder im interstellaren Medium und um Galaxien |
| 50 μT | Erdmagnetfeld in Deutschland |
| 0,1 mT | Zulässiger Grenzwert für elektromagnetische Felder bei 50 Hz (Haushaltsstrom) in Deutschland gemäß der 26. BImSchV |
| 2 mT | In 1 cm Abstand von einem 100-A-Strom, z.B. Batteriestrom beim Anlassen eines Pkw, siehe Ampèresches Gesetz |
| 0,1 T | Handelsüblicher Hufeisenmagnet |
| 0,25 T | Typischer Sonnenfleck |
| 1,61 T | Maximale Flussdichte eines NdFeB-Magneten. NdFeB-Magnete sind die stärksten Dauermagnete, typische Flussdichten sind 1 T bis 1,5 T. |
| 2,45 T | Sättigungspolarisation von Fe65Co35, der höchste Wert eines Materials bei Raumtemperatur. |
| 0,35 bis 3,0 T | Kernspintomograph für die Anwendung am Menschen. Zu Forschungszwecken werden auch Geräte mit 7,0 T und mehr verwendet |
| 8,6 T | Supraleitende Dipolmagnete des Large Hadron Collider des CERN in Betrieb |
| 12 T | Supraleitende Niob-Zinn Spule des ITER Kernfusion-Projektes |
| 28,2 T | Derzeit stärkster supraleitender Magnet in der NMR-Spektroskopie (1,2 GHz-Spektrometer) |
| 32 T | Stärkster Magnet auf Basis von (Hochtemperatur-)Supraleitern |
| 45,5 T | Stärkster dauerhaft arbeitender Elektromagnet, Hybrid aus supraleitendem und konventionellen Elektromagneten |
| 100 T | Pulsspule – höchste Flussdichte ohne Zerstörung der Kupferspule, erzeugt für wenige Millisekunden |
| 1200 T | Höchste durch elektromagnetische Flusskompression erzeugte Flussdichte (kontrollierte Zerstörung der Anordnung, im Labor) |
| 2800 T | Höchste durch explosiv getriebene Flusskompression erzeugte Flussdichte (im Freien) |
| 1 bis 100 MT | Magnetfeld auf einem Neutronenstern |
| 1 bis 100 GT | Magnetfeld auf einem Magnetar |
Literatur
- K. Küpfmüller, G. Kohn: Theoretische Elektrotechnik und Elektronik, Eine Einführung. 16., vollst. neu bearb. u. aktualisierte Auflage. Springer, 2005, ISBN 3-540-20792-9


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.01. 2025