
Lorentzkraft

Die Lorentzkraft ist die Kraft, die eine Ladung in einem magnetischen oder elektrischen Feld erfährt. Ein Magnetfeld übt dabei Kraft auf bewegte Ladungen aus, während ein elektrisches Feld auf bewegte und unbewegte Ladungen gleichermaßen wirkt. Sie ist nach dem niederländischen Mathematiker und Physiker Hendrik Antoon Lorentz benannt.
Die magnetische Komponente der Kraft ist am größten, wenn die Bewegungsrichtung der Ladung senkrecht zu den magnetischen Feldlinien verläuft, und gleich Null, wenn die Ladung sich entlang einer Feldlinie bewegt. Sie wirkt immer senkrecht zur Bewegungsrichtung der Ladung und zu den Magnetfeldlinien. Ihre Wirkungsrichtung kann mit der Drei-Finger-Regel bestimmt werden. Für negative Ladungen verwendet man die linke, für positive Ladungen die rechte Hand.
Eine Erklärung der Lorentzkraft, die letztlich auf die elektrostatische Anziehung zurückgeführt wird, liefert die Spezielle Relativitätstheorie.
Geschichte
Die Form des Induktionsgesetzes in On physical lines of force (1861) oder Eine dynamische Theorie des elektromagnetischen Feldes (1864) von James Clerk Maxwell enthält aus heutiger Sicht einen Anteil, der als Vorläufer der Lorentzkraft betrachtet werden kann. Die eigentliche Behandlung der auf bewegte Punktladungen in Magnetfeldern wirkenden Kräfte erfolgte erst 1881 durch J. J. Thomson. Bei ihm tritt noch ein fehlerhafter Vorfaktor ½ auf. Die korrekte Form der Lorentzkraft leiteten Oliver Heaviside (1889) und Hendrik Antoon Lorentz (1895) ab.
Allgemeine Definition
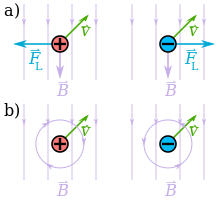
b) Störung des magnetischen Feldes durch die bewegten Ladungsträger. Die Teilchen bewegen sich hier in die Zeichenebene hinein, das Feld und die Kraft liegen in der Zeichenebene.
Bewegt sich eine elektrische Ladung
mit der Geschwindigkeit
durch ein elektromagnetisches
Feld, ist die insgesamt auf die Ladung wirkende Lorentzkraft im weiteren
Sinne:
und
sind dabei die elektrische und magnetische Komponente der Lorentzkraft im
weiteren Sinne,
die elektrische
Feldstärke,
die magnetische
Flussdichte und das Zeichen
das des Vektor-
oder Kreuzprodukts der beteiligten Vektoren.
Der resultierende Vektor eines Kreuzprodukts steht stets senkrecht auf beiden
Ausgangsvektoren, und das Skalarprodukt
orthogonaler
Vektoren ist gleich 0. Daraus ergibt sich für den Fall eines nicht vorhandenen
äußeren elektrischen Felds ():
- Bei der Ablenkung eines Teilchens der Ladung
im räumlich und zeitlich konstanten Magnetfeld wird im Gegensatz zur Ablenkung im elektrischen Feld keinerlei Arbeit verrichtet, die kinetische Energie und damit die Bahngeschwindigkeit bleiben also unverändert, denn
.
- Dies gilt auch für relativistische Teilchen. Tatsächlich jedoch emittieren die Teilchen wegen ihrer Ablenkung Bremsstrahlung und geben dadurch Energie ab.
- Verlaufen die Vektoren
und
parallel oder antiparallel zueinander, wird
gleich 0. Bewegt sich eine Ladung
in Feldlinienrichtung eines Magnetfelds oder genau entgegengerichtet, findet also keinerlei Ablenkung statt.
Betrachtet man dagegen, wie in älteren Physik-Lehrbüchern üblich, als
Lorentzkraft im engeren Sinne allein die magnetische Komponente der
obigen Gesamtkraft ,
gilt für ihre Berechnung entsprechend die Formel:
Die in solchem Fall ebenfalls separat betrachtete elektrische Komponente der Lorentzkraft im weiteren Sinne wird dann als Coulombkraft bezeichnet und wie folgt berechnet:
Die Formelzeichen
und
bzw.
und
bezeichnen dabei jeweils einander Entsprechendes, wobei man der Klarheit der
Schreibweise wegen nach Möglichkeit die eine oder die andere Konvention
beibehalten sollte.
Formulierung der Lorentzkraft im cgs/Gauß-System
Im Unterschied zu der obigen Schreibweise der Formel für die Lorentzkraft
,
die auf dem in der Elektrotechnik und den experimentellen Naturwissenschaften
üblichen Internationalen
Maßsystem basiert, schreibt man in der theoretischen Physik und allgemeiner
besonders in England und den USA für dieselbe Kraft in den äquivalenten, aber
leicht verschiedenen cgs-Einheiten
bzw. für die Lorentzkraft im weiteren Sinn
wobei die Größen
und
sowie
den entsprechenden SI-Größen weitgehend äquivalent sind, man sie also der
Einfachheit halber meist ohne spezielle Indizes ebenfalls als
und
sowie
bezeichnet. Es gelten jedoch die Transformationsformeln:
mit der dimensionsbehafteten Dielektrizitätskonstanten
im Vakuum
(für die systematische Umrechnung von Größen in SI-Einheiten ins cgs-System und
umgekehrt siehe den entsprechenden Abschnitt im Artikel über die Maxwellschen
Gleichungen).
Doppeldeutige Bezeichnung
Die Bezeichnung „Lorentzkraft“ wird nicht einheitlich verwendet. Ältere
Lehrwerke
unterscheiden meist zwischen der Lorentzkraft im engeren Sinne
und der Coulombkraft
.
Erstere wird von magnetischen Feldern auf bewegte Ladungen ausgeübt, letztere
von elektrischen Feldern auf bewegte oder unbewegte Ladungen. Die neuere
Literatur fasst beide Kräfte meist als magnetische Komponente
und elektrische Komponente
der Gesamtkraft
,
der Lorentzkraft im weiteren Sinne, auf.
Lorentzkraft auf bewegte Punktladungen
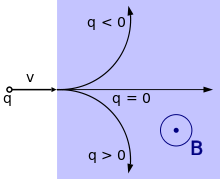
Als bewegte Punktladungen werden kleine freie Ladungen wie etwa Elektronen, Protonen oder andere geladene Elementarteilchen, z.B. Alphateilchen, aber auch Ionen betrachtet, die sich frei im Raum, z.B. im Vakuum oder in einer Salzlösung, bewegen können.
Da die Richtung der Lorentzkraft vom Vorzeichen der Ladung
abhängt, werden entgegengesetzt geladene Punktladungen gleicher
Bewegungsrichtung in entgegengesetzte Richtungen abgelenkt. Bewegen sich die
entgegengesetzt geladenen Punktladungen dagegen außerdem (z.B. in einer
Salzlösung, an die man eine elektrische Spannung gelegt hat) in entgegengesetzte
Richtungen, ist die Richtung ihrer magnetischen Ablenkung wieder dieselbe
(siehe nebenstehende Abbildungen).
Der Betrag der Lorentzkraft ergibt sich dabei aus
zu
mit
als dem Winkel
zwischen der Bewegungsrichtung von q und der Richtung des Magnetfelds
bzw. seiner Flussdichte
.
Bewegt sich die Punktladung genau senkrecht zum Magnetfeld, gilt ,
also:
-
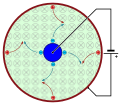 Magnetische Ablenkung der Ionen versetzt eine Salzlösung in Rotation.
Magnetische Ablenkung der Ionen versetzt eine Salzlösung in Rotation. -
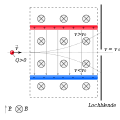 Der Geschwindigkeitsfilter nach Wien beruht auf Kräftegleichgewicht zwischen Lorentzkraft und Coulombkraft.
Der Geschwindigkeitsfilter nach Wien beruht auf Kräftegleichgewicht zwischen Lorentzkraft und Coulombkraft.
Lorentzkraft am stromdurchflossenen Leiter
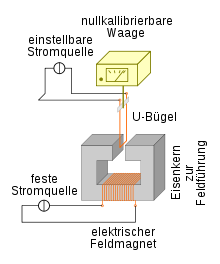
Die Lorentzkraft ist das zentrale Bindeglied zwischen Elektrizität und Mechanik. Fließt Strom durch einen Leiter, der quer oder schräg zu den Feldlinien eines ihn umgebenden Magnetfelds liegt, dann lässt sich eine Kraftwirkung auf den Leiter feststellen. Die Auslenkung im Leiterschaukelversuch oder die Messungen beim Stromwaagen-Experiment verdeutlichen dies. Die Kraftwirkung leitet sich dabei aus der auf eine bewegte Punktladung wirkenden Lorentzkraft her; diese wirkt auf die einzelnen Ladungsträger im Leiter.
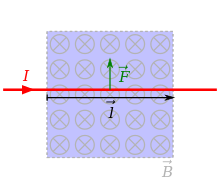
Um die genannten Vorgänge rechnerisch zu erfassen, werde der Einfachheit
halber zunächst ein gerades Stück Draht der gerichteten Länge
betrachtet, das in einem zeitlich konstanten homogenen äußeren Magnetfeld der
Flussdichte
liegt. Durch den Draht fließe ein ebenfalls zeitlich konstanter Strom der Stärke
,
sodass seine Leitungselektronen sich mit der gleichbleibenden Geschwindigkeit
durch den Draht bewegen und dabei in der Laufzeit
die Gesamtladung
mit der Geschwindigkeit
transportieren. Wegen
ist damit die Summe der Lorentzkräfte auf alle am Stromfluss beteiligten
Leitungselektronen und damit auf das Drahtstück als Ganzes
Die zugehörige Betragsgleichung lautet dann
mit
als dem Winkel
zwischen der Längsrichtung des Drahtes und der Richtung der magnetischen
Flussdichte
.
Verläuft der Draht genau senkrecht zum Magnetfeld, ist
und die Gleichung vereinfacht sich zu
Für gekrümmte Leiter muss die Kraftwirkung durch Integration berechnet
werden, indem das Magnetfeld nur für infinitesimal kleine Stücke
des Leiters als konstant angesehen wird. Damit ergibt sich folgende Formel:
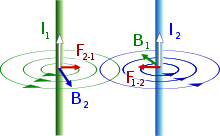
Kraft zwischen zwei stromdurchflossenen Leitern
Verknüpft man die Formel für die Lorentzkraft auf stromdurchflossene Leiter mit dem Biot-Savart-Gesetz für das Magnetfeld um stromdurchflossene Leiter, so ergibt sich eine Formel für die Kraft, die zwei stromdurchflossene dünne Leiter aufeinander ausüben, was in der Literatur auch als ampèresches Kraftgesetz (nicht zu verwechseln mit dem ampèreschen Gesetz) bezeichnet wird.
Wenn die beiden Leiter dünn sind und einander parallel gegenüberliegen wie
die gegenüberliegenden Seiten eines Rechtecks,
dann ergibt sich die schon von der Ampère-Definition
her bekannte einfache Formel für den Kraftbetrag
der aufeinander wirkenden (nach dem Wechselwirkungsprinzip
gleich großen) Kräfte:
Dabei ist
die (bei beiden Leitern gleich große) Länge der Leiter,
ihr gegenseitiger Abstand und
sind die Stromstärken in den beiden Leitern.
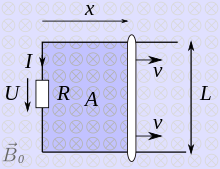
Elektromagnetische Induktion
Des Weiteren erklärt die Lorentzkraft die Umwandlung mechanischer Bewegung in elektrische Spannung. Dabei ergibt sich mittels der Lorentzkraft eine alternative Herleitung der elektromagnetischen Induktion statt über die Flussänderung.
Der Einfachheit halber sei wieder ein gerades Stück Draht der Länge
betrachtet, das nun mit der konstanten Geschwindigkeit
quer durch ein senkrecht zu ihm verlaufendes zeitlich konstantes
homogenes äußeres Magnetfeld der Flussdichte
geschoben werde, also so, dass die Längsrichtung des Drahtes dabei außerdem
senkrecht auf
steht.
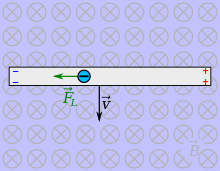
Wie weiter oben erläutert, halten sich in diesem Fall zwei Kräfte die Waage,
zum einen die Lorentzkraft ,
die die Leitungselektronen des Drahtes in Richtung eines seiner beiden Enden
verschiebt, zum anderen die auf die Leitungselektronen wirkende Coulombkraft
aufgrund der durch die Ladungstrennung zwischen beiden Leiterenden induzierten
elektrischen Spannung:
Herauskürzen der, wie zu sehen, hier gänzlich unerheblichen Gesamtladung
und skalare
Multiplikation mit dem Vektor der gerichteten Leiterlänge
liefert schlussendlich die Gleichung für die gesuchte Induktionsspannung
:
Sind die drei Vektoren, wie eingangs verlangt, paarweise senkrecht zueinander, vereinfacht sich das Spatprodukt l·(v×B), sodass sich die bekannte Formel
ergibt.
Lenzsche Regel
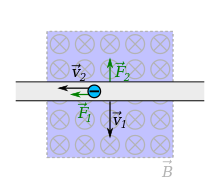
Überbrückt man nun beide Enden des bewegten Leiters mit einem ohmschen
Widerstand der Größe R, der dagegen nicht gegenüber dem Magnetfeld bewegt wird,
entsteht eine geschlossene Leiterschleife, über die sich die Induktionsspannung
ausgleichen kann, sodass diese und das Produkt
also gemäß der Kirchhoffschen
Maschenregel die Summe 0 liefern:
Der durch den geschlossenen Stromkreis fließende Strom erzeugt nun wieder eine Lorentzkraft, die der Bewegungsrichtung entgegenwirkt. Die Lorentzkraft erklärt somit nicht nur die Ladungstrennung, mit der die Induktionsspannung entsteht, sondern zudem die Gegenkraft, die Teil der Lenzschen Regel ist.
In gleicher Weise erzeugen Generatoren Spannung und lassen Ströme fließen, wodurch sie mechanische in elektrische Leistung umformen. Beim Elektromotor sind Spannung und Strom so gerichtet, dass er elektrische Leistung aufnimmt und als verrichtete Arbeit abgibt.
Wirkungsprinzip
Die Lorentzkraft ergibt sich in der lagrangeschen Formulierung der Bewegung
eines geladenen Teilchens der Ladung
und der Masse
aus der Lagrangefunktion
.
Hierbei sind
und
das skalare Potential und das Vektorpotential,
die zu der elektrischen Feldstärke
und der magnetischen Flussdichte
gehören.
Das Prinzip der stationären Wirkung führt auf die Euler-Lagrange-Gleichungen
.
Die Auswertung der in den Nabla-Operatoren vorkommenden partiellen Ableitungen liefert:
Dabei ist der erste Term in den runden Klammern der (kinetische) Impuls (während
der gesamte Ausdruck in den ersten runden Klammern den generalisierten
Impuls beschreibt) eines sich mit der Geschwindigkeit
bewegenden Teilchens:
Die totale
zeitliche Ableitung des Vektorpotentials, das explizit von der Zeit und von
allen Ortskoordinaten abhängig ist, lautet unter Benutzung der Vektorrelation
:
Eingesetzt ergibt sich:
Somit erhält man die Bewegungsgleichung in Abhängigkeit von E und B:
Beispiele
Historische Definition der Maßeinheit Ampere
Die Lorentzkraft war von 1948 bis 2019 Grundlage der international gültigen Definition der SI-Basiseinheit Ampere:
- Ein Ampere ist „die Stärke eines zeitlich unbegrenzt unveränderlichen
elektrischen Stroms, der durch zwei parallel im Abstand von 1 m im Vakuum
angeordnete geradlinige, unendlich lange Leiter mit vernachlässigbar kleinem,
kreisförmigen Querschnitt fließend, elektrodynamisch die Kraft von
N je m Leiterlänge zwischen diesen Leitern hervorrufen würde.“
Der Betrag der Kraft ergibt sich nach dem Ampèreschen
Kraftgesetz für zwei gerade, benachbarte und dünne Linienleiter. Bei zwei
Leitern, die jeweils vom Strom
bzw.
mit einem gegenseitigen Abstand
durchflossen werden, beträgt die längenbezogene magnetische Lorentzkraft
:
Bei einem Leiterabstand
und einen Strom von
ergibt sich pro Meter Leiterlänge die Kraft von
aus obiger Definition. Die resultierende Kraft ist hier anziehend, bei
entgegengesetzt gerichteten Strömen wäre sie abstoßend.
Technische Anwendungen der Lorentzkraft
- Rotierende elektrische Maschinen wie der Elektromotor und der elektrische Generator
- Ablenkmagnete und Ablenksysteme zur Fokussierung und Ablenkung von geladener Teilchenstrahlung (zum Beispiel in der Kathodenstrahlröhre, in Bildröhren, in allen Kreisbeschleunigern)
- In magnetfeldabhängigen Widerständen, wie in der Feldplatte, beim Hall-Effekt und den darauf basierenden Hall-Sensoren
- Massenspektrometrie zur chemischen und physikalischen Analytik
Lorentzkräfte in der Natur
- Die Ablenkung des Sonnenwinds durch das Magnetfeld der Erde im Van-Allen-Gürtel erfolgt durch die Lorentzkraft.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.09. 2023