Biot-Savart-Gesetz

Das Biot-Savart-Gesetz beschreibt das Magnetfeld bewegter Ladungen. Es stellt einen Zusammenhang zwischen der magnetischen Feldstärke ${\vec {H}}$ und der elektrischen Stromdichte ${\vec {j}}$ her und erlaubt die Berechnung räumlicher magnetischer Feldstärkenverteilungen anhand der Kenntnis der räumlichen Stromverteilungen. Hier wird das Gesetz als Beziehung zwischen der magnetischen Flussdichte ${\vec {B}}$ und der elektrischen Stromdichte ${\vec {J}}$ behandelt.

Im Vakuum und in magnetisch linearen und isotropen Stoffen besteht zwischen der magnetischen Flussdichte und der magnetischen Feldstärke der Zusammenhang $\vec B = \mu \vec H$ mit der magnetischen Leitfähigkeit ${\textstyle \mu }$ als konstantem Proportionalitätsfaktor. Im allgemeinen Fall (z.B. bei Magneten) kann hingegen die magnetische Leitfähigkeit eine Funktion der magnetischen Feldstärke oder der räumlichen Orientierung sein, womit sich deutlich kompliziertere und unter Umständen analytisch nicht mehr darstellbare Zusammenhänge ergeben können.

Benannt wurde dieses Gesetz nach den beiden französischen Mathematikern Jean-Baptiste Biot und Félix Savart, die es 1820 formuliert hatten. Es stellt neben dem ampèreschen Gesetz eines der Grundgesetze der Magnetostatik, eines Teilgebiets der Elektrodynamik, dar.

Formulierung

Ein Stromleiter mit dem infinitesimalen Längenelement $\mathrm {d} {\vec {l}}$ am Ort ${\vec r}'$ , der von einem Strom durchflossen wird, erzeugt am Ort ${\vec {r}}$ die magnetische Flussdichte $\mathrm {d} {\vec {B}}$ (unter Verwendung des Kreuzprodukts):

$\mathrm {d} {\vec {B}}({\vec {r}})={\frac {\mu _{0}}{4\pi }}\,I\,\mathrm {d} {\vec {l}}\times {\frac {{\vec {r}}-{\vec {r}}'}{|{\vec {r}}-{\vec {r}}'|^{3}}}$

Die ganze magnetische Flussdichte ergibt sich durch Aufsummieren aller vorhandenen infinitesimalen Anteile, also durch Integrieren. Das entstehende Wegintegral kann man unter Benutzung von

$I\,\mathrm {d} {\vec {l}}={\vec {v}}\,\mathrm {d} q={\vec {v}}\rho \,\mathrm {d} V={\vec {j}}\,\mathrm {d} V$

in ein Volumenintegral umformen, wobei ${\vec {j}}$ die elektrische Stromdichte ist. Somit erhält man die integrale Form des biot-savartschen Gesetzes:

${\vec {B}}({\vec {r}})={\frac {\mu _{0}}{4\pi }}\int _{V}{\vec {j}}({\vec {r}}')\times {\frac {{\vec {r}}-{\vec {r}}'}{|{\vec {r}}-{\vec {r}}'|^{3}}}\;\mathrm {d} {V'}$

Diese beiden Formeln ähneln (mit Strömen statt Ladungen) dem coulombschen Gesetz, das die Gestalt des elektrischen Feldes in Abhängigkeit von einer Ladungsverteilung beschreibt.

In den beiden obigen Formeln wurde dabei vernachlässigt, dass die Stromleiter einen endlichen Querschnitt haben. In vielen realen Anwendungen ist dieser im Vergleich zur Ausdehnung des Magnetfeldes aber auch tatsächlich ohne Bedeutung. Eine weitere Ungenauigkeit besteht darin, dass sich der Beitrag einer Ladung an einem Ort zum Magnetfeld an einem anderen Ort mit Lichtgeschwindigkeit ausbreitet. Der entsprechende Retardierungseffekt wird im Biot-Savart-Gesetz nicht berücksichtigt. Es ist daher nur für stationäre Ströme streng gültig und für Punktladungen in guter Näherung, sofern ihre Geschwindigkeit klein im Vergleich zur Lichtgeschwindigkeit ist.

Ableitung aus den Maxwellgleichungen

Im Folgenden werden Retardierungseffekte vernachlässigt und der zeitlich konstante Fall in Form der Magnetostatik betrachtet. Aus den Maxwellgleichungen folgt dann die Poissongleichung für das Vektorpotential ${\vec {A}}$

$\Delta {\vec {A}}({\vec {r}})=-\mu _{0}{\vec {j}}({\vec {r}})$

mit folgender Lösung:

${\vec {A}}({\vec {r}})={\frac {\mu _{0}}{4\pi }}\int d^{3}r'\,{\frac {{\vec {j}}({\vec {r}}')}{|{\vec {r}}-{\vec {r}}'|}}$

Damit folgt für die magnetische Flussdichte:

${\vec {B}}={\vec {\nabla }}\times {\vec {A}}={\frac {\mu _{0}}{4\pi }}\int d^{3}r'\,\nabla \times \left({\frac {{\vec {j}}({\vec {r}}')}{|{\vec {r}}-{\vec {r}}'|}}\right)$

Mit Hilfe der Formeln ${\vec {\nabla }}\times (\phi {\vec {j}})=\phi ({\vec {\nabla }}\times {\vec {j}})-{\vec {j}}\times ({\vec {\nabla }}\phi )$ für die Anwendung des Rotationsoperators $\nabla \times$ auf ein Produkt aus skalarer Funktion und Vektorfunktion sowie aus

${\vec {\nabla }}\phi ={\vec {\nabla }}\left({\frac {1}{|{\vec {r}}-{\vec {r}}'|}}\right)=-{\frac {{\vec {r}}-{\vec {r}}'}{{|{\vec {r}}-{\vec {r}}'|}^{3}}}$

folgt das Endergebnis, wenn man berücksichtigt, dass ${\vec {\nabla }}$ im Integral nur auf die Variable ${\vec {r}}$ und nicht auf ${\vec r}'$ wirkt. Häufig ist es vorteilhafter, das Vektorpotential zu berechnen und daraus die magnetische Flussdichte.

Zum selben Ergebnis kommt man, indem man die Helmholtz-Zerlegung und die Maxwellgleichungen für den statischen Fall benutzt.

Anwendung

Kreisförmige Leiterschleife

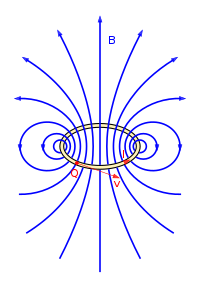
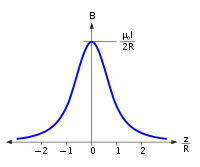
Magnetfeld in einer Stromschleife

Flussdichte ${\vec {B}}$ in Abhängigkeit vom Abstand entlang der Achse der Leiterschleife

Der Betrag der magnetischen Flussdichte einer kreisförmigen, gegen den Uhrzeigersinn durchflossenen Leiterschleife kann mit Hilfe des Biot-Savart-Gesetzes auf der Symmetrieachse senkrecht zur Leiterschleife geschlossen angegeben werden:

$B(z)={\frac {\mu _{0}}{2}}\,{\frac {R^{2}I}{\left(R^{2}+z^{2}\right)^{3/2}}}$

Dabei ist der Radius der in der -Ebene liegenden Leiterschleife. Das Feld ist in ${\vec {e}}_{z}$ -Richtung gerichtet.

Durch die Substitution

$\tan \alpha ={\frac {R}{z}}$

erhält man daraus

$B\left(\alpha \right)={\frac {I\mu _{0}}{2R}}\sin ^{3}{\alpha }.$

Im Fall $R\ll r$ kann das Feld der Leiterschleife als Dipolfeld behandelt werden: Beispielsweise zeigt es für Punkte auf der -Achse für große Abstände (große ) eine ${\tfrac {1}{z^{3}}}$ -Abhängigkeit:

$B={\frac {\mu _{0}m}{2\pi \left|z\right|^{3}}}$

mit dem magnetischen (Dipol-)Moment $m=I\pi R^{2}$ (Strom × Fläche der Leiterschleife).

Gerader Linienleiter

Zur Berechnung der Flussdichte ${\vec {B}}$ eines geraden Linienleiters der Länge $2L$ eignen sich Zylinderkoordinaten. Dabei legt man den Ursprung des Koordinatensystems mittig in den Linienleiter parallel zur -Achse. Die Stromdichte des Linienleiters ist dann ${\vec {j}}({\vec {r}}')=I{\tfrac {1}{\rho '}}\delta (\rho ')\delta (\varphi ')\Theta (L-|z'|){\vec {e}}_{z}$ mit der Delta-Distribution $\delta$ und der Heaviside-Funktion $\Theta$ . Dadurch vereinfacht sich das Volumenintegral des Biot-Savart-Gesetzes auf ein einfaches Integral über und das Vektorpotential folgt zu:

${\vec {A}}({\vec {r}})={\frac {\mu _{0}I}{4\pi }}\int _{-L}^{L}\mathrm {d} z'{\frac {{\vec {e}}_{z}}{\sqrt {\rho ^{2}+(z'-z)^{2}}}}$

Im Fall des Linienleiters ist es einfacher, zuerst die Rotation zu bilden und dann zu integrieren. Da das Vektorpotential nur eine -Komponente aufweist und diese nicht von $\varphi$ abhängt, ist diese

${\vec {B}}={\vec {\nabla }}\times {\vec {A}}=-{\frac {\partial A_{z}}{\partial \rho }}{\vec {e}}_{\varphi }={\frac {\mu _{0}I}{4\pi }}\int _{-L}^{L}\mathrm {d} z'\,{\frac {\rho }{{\sqrt {\rho ^{2}+(z'-z)^{2}}}^{3}}}{\vec {e}}_{\varphi }$ .

Die Substitution $\tan \xi ={\tfrac {z'-z}{\rho }}$ liefert mit $\mathrm {d} z'=\rho {\tfrac {1}{\cos ^{2}\xi }}\mathrm {d} \xi$ dann

${\vec {B}}({\vec {r}})={\frac {\mu _{0}I}{4\pi }}\int _{\arctan {\frac {-L+z}{\rho }}}^{\arctan {\frac {L+z}{\rho }}}\mathrm {d} \xi {\frac {\cos \xi }{\rho }}{\vec {e}}_{\varphi }={\frac {\mu _{0}I}{4\pi \rho }}\left(\sin \arctan {\frac {L+z}{\rho }}+\sin \arctan {\frac {L-z}{\rho }}\right){\vec {e}}_{\varphi }$ .

${\vec {B}}$ -Feld eines geraden Leiters

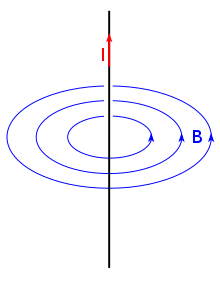
Der Fall eines unendlich langen geraden Linienleiters ergibt sich aus dem Grenzfall des geraden Leiters mit $L\to \infty$ .

${\vec {B}}({\vec {r}})={\frac {\mu _{0}I}{2\pi \rho }}{\vec {e}}_{\varphi }$

Dabei hängt die magnetische Flussdichte nur noch vom radialen Abstand des Punktes zum Leiter ab, da aus der Translationssymmetrie die Abhängigkeit von verschwinden muss.

Rahmenspule

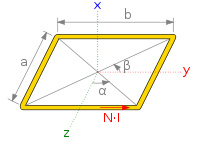
Abhängigkeiten zur Berechnung der Rahmenspule

Nach der runden Spule ist die Rahmenspule (mit Windungen) die am häufigsten verwendete Variante. Die Formel für das Magnetfeld im Zentrum kann aus der Formel für den Linienleiter abgeleitet werden, indem man die geraden Abschnitte der Spule als Linienleiter behandelt.

${\vec {B}}={\frac {\mu _{0}\,N\,I}{4\,\pi }}\,2\,\left({\frac {2\,\sin {\alpha }}{\frac {a}{2}}}+{\frac {2\,\sin {\beta }}{\frac {b}{2}}}\right)\,{\vec {\hat {x}}}$

${\vec {B}}={\frac {\mu _{0}\,N\,I}{\pi }}\,2\,\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)^{\frac {1}{2}}\,{\vec {\hat {x}}}$

mit

$\sin{\alpha} = \frac{b}{\left( a^2 + b^2 \right)^\frac{1}{2}}$

$\sin{\beta} = \frac{a}{\left( a^2 + b^2 \right)^\frac{1}{2}}$

Für das Magnetfeld auf der -Achse, in großem Abstand von der Spule, ergibt sich

$B={\frac {\mu _{0}\,N\,I\,a\,b}{2\,\pi x^{3}}},$

also wieder eine Abhängigkeit wie beim Dipol. Mit magnetischem Moment $m=NIab$ gilt:

$B = \frac{\mu_0 m} {2\,\pi x^3}$

Punktladung mit konstanter Geschwindigkeit

Im Falle einer Punktladung , die sich mit konstanter Geschwindigkeit ${\vec {v}}$ gemäß der Maxwell-Gleichungen bewegt, gelten für das elektrische und das magnetische Feld die Gleichungen

${\vec {E}}={\frac {q}{4\pi \varepsilon _{0}}}{\frac {1-v^{2}/c^{2}}{(1-v^{2}\sin ^{2}\theta /c^{2})^{3/2}}}{\frac {\vec {{\hat {r}}'}}{|{\vec {r'}}|^{2}}},$

${\vec {H}}={\vec {v}}\times {\vec {D}}$ oder umgeformt

${\vec {B}}={\frac {1}{c^{2}}}{\vec {v}}\times {\vec {E}},$

worin ${\vec {{\hat {r}}'}}$ der Einheitsvektor ist, der von der momentanen (nicht-retardierten) Position des Teilchens zu dem Punkt zeigt, in dem das Feld gemessen wird, und $\theta$ der Winkel zwischen ${\vec {v}}$ und ${\vec r}'$ .

Im Fall $v^2 \ll c^2$ können das elektrische und das magnetische Feld näherungsweise wie folgt angegeben werden:

${\vec {E}}={\frac {q}{4\pi \varepsilon _{0}}}\ {\frac {\vec {{\hat {r}}'}}{|{\vec {r}}'|^{2}}}$

${\vec {B}}={\frac {\mu _{0}q}{4\pi }}{\vec {v}}\times {\frac {\vec {{\hat {r}}'}}{|{\vec {r}}'|^{2}}}$

Diese Gleichungen werden (wegen der Analogie mit dem „normalen“ Biot–Savart-Gesetz) „Biot–Savart-Gesetz für eine Punktladung“ genannt. Sie wurden zuerst von Oliver Heaviside im Jahre 1888 hergeleitet.

Siehe auch

Magnetismus

Literatur

Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. 14. Auflage. Springer, Berlin 1993, ISBN 3-540-56500-0.
Klaus Dransfeld, Paul Kienle: Physik II. Elektrodynamik. Oldenbourg 1975.
Thorsten Fließbach: Elektrodynamik. Siegen 1993.

Basierend auf einem Artikel in:

Wikipedia.de