Ampèresches Kraftgesetz

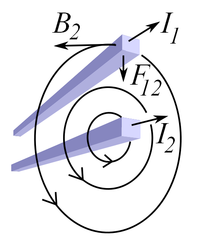
Der obere Draht mit Stromstärke I₁ erfährt eine Lorentzkraft F₁₂ aufgrund des Magnetfelds B₂, das der untere Draht erzeugt. (Der spiegelbildliche Sachverhalt für die Lorentzkraft auf den unteren Draht ist nicht eingezeichnet.)

Nach dem Biot-Savart-Gesetz existiert um einen stromdurchflossenen Leiter ein Magnetfeld und auf einen zweiten stromdurchflossenen Leiter bewirkt dies eine Lorentzkraft, also üben zwei stromdurchflossene Leiter eine Kraft aufeinander aus. Diese Beziehung wird in der Literatur auch als ampèresches Kraftgesetz bezeichnet – nicht zu verwechseln mit dem ampèreschen Gesetz (welches auch Durchflutungsgesetz genannt wird).

Historische Entwicklung

Nachdem Hans Christian Oersted Anfang 1820 aufzeigte, dass ein stromdurchflossener Draht eine Kompassnadel beeinflusst, also ein Magnetfeld besitzt und Jean-Baptiste Biot und Félix Savart noch im selben Jahr dazu die Beziehung zwischen Stromfluss und Magnetfeld (Biot-Savart-Gesetz) formulierten, entdeckte André-Marie Ampère im gleichen Jahr, dass zwischen parallelen Strömen eine Kraft auftritt. Er stellte sein Gesetz dazu 1826 in seinem Werk Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l'expérience in differentieller Form auf. Ampères differentielle Fassung unterscheidet sich von der heute gebräuchlichen differentiellen Fassung durch Hermann Graßmann, im Experiment kann kein Unterschied entdeckt werden, weil dort immer geschlossene Stromkreise vorliegen und in der integralen Fassung liefern beide Formulierungen dasselbe Ergebnis. Im Folgenden wird die heute gebräuchliche Formulierung nach Graßmann verwendet, obwohl die Formulierung nach Ampère den Vorzug hat, dass sie auch in ihrer differentiellen Form mit dem Wechselwirkungsgesetz verträglich ist, was für die Graßmanns Formulierung nicht gilt. Letztere hat aber den Vorteil, dass sie sich heute leicht aus dem Biot-Savart-Gesetz und der Lorentzkraft herleiten lässt.

Integralformel für zwei dünne Leiter

Verwendet man die differentielle Formulierung von Graßmann und integriert sie, ergibt sich für die Kraft ${\vec {F}}_{{12}}$ , die vom stromdurchflossenen dünnen Leiter 2 auf den stromdurchflossenen dünnen Leiter 1 ausgeübt wird:

${\vec {F}}_{12}={\frac {\mu _{0}}{4\pi }}I_{1}I_{2}\int _{L_{1}}\int _{L_{2}}{\frac {{\text{d}}{\vec {\ell }}_{1}\ \times \ ({\text{d}}{\vec {\ell }}_{2}\ \times \ {\vec {r}}_{21})}{r^{3}}}$

wobei

$\mu _{0}$ die magnetische Feldkonstante ist,
$I_{1}$ und $I_{2}$ die Stromstärken in Leiter 1 bzw. 2 sind,
${\text{d}}{\vec {\ell }}_{1}$ und ${\text{d}}{\vec {\ell }}_{2}$ die (infinitesimal kleinen) vektoriellen Linienelemente am Ort $\vec{r}_1$ bzw. $\vec{r}_2$ (also ${\text{d}}{\vec {\ell }}_{i}={\text{d}}{\vec {r}}_{i}$ ) der beiden Leiter sind, über die im doppelten Linienintegral längs der Kurven $L_{1}$ und integriert wird,
${\vec {r}}_{21}={\vec {r}}_{1}-{\vec {r}}_{2}$ der Vektor ist, der vom Ort des Linienelements des Leiters 2 zum Ort des Linienelements des Leiters 1 zeigt,
$r=|{\vec {r}}_{21}|$ der Abstand zwischen den beiden Linienelementen ist,
$\times$ das Zeichen für das Kreuzprodukt (Vektorprodukt) ist und
die Stromstärken $I_{1}$ bzw. $I_{2}$ im Leiter 1 bzw. Leiter 2 konstant sind. Ihre Vorzeichen sind relativ zur Orientierung von ${\text{d}}{\vec {\ell }}_{1}$ bzw. ${\text{d}}{\vec {\ell }}_{2}$ zu betrachten; wenn also $I_{1}>0$ ist, zeigt das Linienelement ${\text{d}}{\vec {\ell }}_{1}$ immer in Richtung der technischen Stromrichtung, worauf bei der Parametrisierung der Kurven ${\vec {r}}_{i}(t)$ geachtet werden muss.

Für die Kraft ${\vec {F}}_{21}$ , die vom stromdurchflossenen dünnen Leiter 1 auf den stromdurchflossenen dünnen Leiter 2 ausgeübt wird, gilt nach dem Wechselwirkungsgesetz: ${\vec {F}}_{21}=-{\vec {F}}_{12}$

Voraussetzungen für die Gültigkeit der Formel:

Die Drähte sind ungeladen.
Die Stromstärke durch die Drähte ist konstant.
Die Drähte sind (ideal) dünn und bewegen sich nicht.

Differentielle Formulierungen

Differentielle Formulierung nach Graßmann:

${\text{d}}^{2}{\vec {F}}_{12}^{(G)}={\frac {\mu _{0}}{4\pi }}I_{1}I_{2}{\frac {{\text{d}}{\vec {\ell }}_{1}\times ({\text{d}}{\vec {\ell }}_{2}\times {\vec {r}}_{21})}{r^{3}}}$

Löst man das doppelte Kreuzprodukt mit der Graßmann-Identität auf, ergibt sich:

${\text{d}}^{2}{\vec {F}}_{12}^{(G)}=-{\frac {\mu _{0}}{4\pi }}{\frac {I_{1}I_{2}}{r^{3}}}\left({\vec {r}}_{21}({\text{d}}{\vec {\ell }}_{1}\cdot {\text{d}}{\vec {\ell }}_{2})-{\text{d}}{\vec {\ell }}_{2}({\text{d}}{\vec {\ell }}_{1}\cdot {\vec {r}}_{21})\right)$

Differentielle Formulierung nach Ampère:

${\text{d}}^{2}{\vec {F}}_{12}^{(A)}=-{\frac {\mu _{0}}{4\pi }}{\frac {I_{1}I_{2}}{r^{3}}}{\vec {r}}_{21}\left(2{\text{d}}{\vec {\ell }}_{1}\cdot {\text{d}}{\vec {\ell }}_{2}-3{\frac {{\vec {r}}_{21}\cdot {\text{d}}{\vec {\ell }}_{1}}{r}}{\frac {{\vec {r}}_{21}\cdot {\text{d}}{\vec {\ell }}_{2}}{r}}\right)$

wobei $\cdot$ hier das Zeichen für das Skalarprodukt ist.

Nun gilt ${\text{d}}^{2}{\vec {F}}_{21}^{(A)}=-{\text{d}}^{2}{\vec {F}}_{12}^{(A)}$ , denn ${\vec {r}}_{21}=-{\vec {r}}_{12}$ und der Ausdruck in der Klammer ist symmetrisch unter Vertauschung der Indizes. Das heißt, bereits die differentielle Form ${\text{d}}^{2}{\vec {F}}_{12}^{(A)}$ ist mit dem Wechselwirkungsgesetz verträglich, wohingegen dies für ${\text{d}}^{2}{\vec {F}}_{12}^{(G)}$ nicht gilt.

Verknüpfung von Lorentzkraft und Biot-Savart

Für die Lorentzkraft auf den dünnen stromdurchflossenen Leiter 1 gilt:

${\vec {F}}_{L}=I_{1}\int _{L_{1}}\left({\text{d}}{\vec {\ell }}_{1}\times {\vec {B}}_{2}({\vec {r}}_{1})\right)$ , wobei ${\vec {B}}_{2}({\vec {r}}_{1})$ das Magnetfeld des stromdurchflossenen Leiters 2 am Ort $\vec{r}_1$ ist

Nach dem Gesetz von Biot-Savart gilt unter der Voraussetzung, dass Leiter 2 dünn ist:

${\vec {B}}_{2}({\vec {r}}_{1})={\frac {\mu _{0}I_{2}}{4\pi }}\int _{L_{2}}{\frac {{\text{d}}{\vec {\ell }}_{2}\times {\vec {r}}_{21}}{r^{3}}}$

Setzt man ${\vec {B}}_{2}({\vec {r}}_{1})$ in die obere Formel ein, ergibt sich:

${\vec {F}}_{L}=I_{1}\int _{L_{1}}\left({\text{d}}{\vec {\ell }}_{1}\times \left({\frac {\mu _{0}I_{2}}{4\pi }}\int _{L_{2}}{\frac {{\text{d}}{\vec {\ell }}_{2}\times {\vec {r}}_{21}}{r^{3}}}\right)\right)$

Und nach Herausziehen des skalaren und konstanten Faktors ${\frac {\mu _{0}I_{2}}{4\pi }}$ folgt also:

${\vec {F}}_{L}={\frac {\mu _{0}I_{1}I_{2}}{4\pi }}\int _{L_{1}}\left({\text{d}}{\vec {\ell }}_{1}\times \int _{L_{2}}{\frac {{\text{d}}{\vec {\ell }}_{2}\times {\vec {r}}_{21}}{r^{3}}}\right)$

Da Integral und Kreuzprodukt lineare Operatoren sind, gilt damit (absolute Integrierbarkeit vorausgesetzt):

${\vec {F}}_{L}={\frac {\mu _{0}I_{1}I_{2}}{4\pi }}\int _{L_{1}}\int _{L_{2}}{\frac {{\text{d}}{\vec {\ell }}_{1}\times ({\text{d}}{\vec {\ell }}_{2}\times {\vec {r}}_{21})}{r^{3}}}$

Spezialfall für parallele Leiter

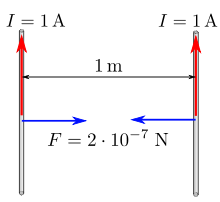
Veranschaulichung der historischen Definition des Ampere (1948–2019)

Wenn die beiden Leiter gerade, dünn, parallel und unendlich lang sind, ergibt sich für den Betrag der aufeinander wirkenden Kräfte ${\vec {F}}_{{12}}$ bzw. ${\vec {F}}_{21}$ :

${\frac {F}{\ell }}={\frac {\mu _{0}}{2\pi }}\cdot {\frac {I_{1}\cdot I_{2}}{r}}.$

Dabei ist ${\frac {F}{\ell }}$ die Kraft bezogen auf ein Leiterstück der Länge $\ell$ , der Abstand der Leiter und $I_{1}$ bzw. $I_{2}$ sind die Stromstärken in Leiter 1 bzw. 2. Bis 2019 war das Ampere so definiert, dass bei Strömen I₁ = I₂ = 1 A die Kraft pro Leiterstrück 2·10⁻⁷ N/m beträgt, also generell:

${\frac {F}{\ell }}=2\cdot 10^{-7}{\frac {\text{N}}{{\text{A}}^{2}}}\cdot {\frac {I_{1}\cdot I_{2}}{r}}\,.$

Seit der Revision des SI gilt diese Beziehung nicht mehr exakt, aber in extrem guter Näherung.

Basierend auf einem Artikel in:

Wikipedia.de