
Ortsvektor
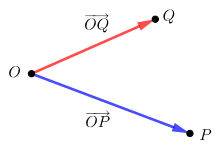
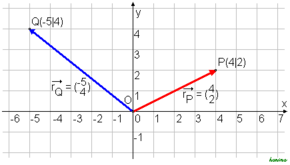
Als Ortsvektor (auch Radiusvektor oder Positionsvektor) eines Punktes bezeichnet man in der Mathematik und in der Physik einen Vektor, der von einem festen Bezugspunkt zu diesem Punkt (Ort) zeigt. In der elementaren und in der synthetischen Geometrie können diese Vektoren als Klassen von verschiebungsgleichen Pfeilen oder gleichwertig als Parallelverschiebungen definiert werden.
Ortsvektoren ermöglichen es, für die Beschreibung von Punkten, von Punktmengen und von Abbildungen die Vektorrechnung zu benutzen. Legt man ein kartesisches Koordinatensystem zugrunde, dann wählt man in der Regel den Koordinatenursprung als Bezugspunkt für die Ortsvektoren der Punkte. In diesem Fall stimmen die Koordinaten eines Punktes bezüglich dieses Koordinatensystems mit den Koordinaten seines Ortsvektors überein.
In der analytischen Geometrie werden Ortsvektoren verwendet, um Abbildungen eines affinen oder euklidischen Raums zu beschreiben und um Punktmengen (wie zum Beispiel Geraden und Ebenen) durch Gleichungen und Parameterdarstellungen zu beschreiben.
In der Physik werden Ortsvektoren verwendet, um den Ort eines Körpers in einem euklidischen Raum zu beschreiben. Ortsvektoren zeigen bei Koordinatentransformationen ein anderes Transformationsverhalten als kovariante Vektoren.
Schreibweisen
In der Geometrie wird der Bezugspunkt (Ursprung) in der Regel mit
(für lat. origo) bezeichnet. Die Schreibweise für den Ortsvektor eines
Punktes
ist dann:
Gelegentlich werden auch die Kleinbuchstaben mit Vektorpfeil benutzt, die den Großbuchstaben entsprechen, mit denen die Punkte bezeichnet werden, zum Beispiel:
Auch die Schreibweise, dass der Großbuchstabe, der den Punkt bezeichnet, mit einem Vektorpfeil versehen wird, ist üblich:
Vor allem in der Physik wird der Ortsvektor auch Radiusvektor genannt
und mit Vektorpfeil als
oder (insbesondere in der theoretischen Physik) halbfett als
geschrieben.
Beispiele und Anwendungen in der Geometrie
Verbindungsvektor
Für den Verbindungsvektor
zweier Punkte
und
mit den Ortsvektoren
und
gilt:
Kartesische Koordinaten
Für die Koordinaten des Ortsvektors
des Punktes
mit den Koordinaten
gilt:
Verschiebung
Eine Verschiebung
um den Vektor
bildet den Punkt
auf den Punkt
ab. Dann gilt für die Ortsvektoren:
Drehung um den Ursprung
Eine Drehung in der Ebene mit
Drehzentrum
gegen den Uhrzeigersinn
kann in kartesischen Koordinaten wie folgt mit Hilfe einer Drehmatrix beschrieben
werden: Ist
der Ortsvektor eines Punktes
und
der Ortsvektor des Bildpunkts
,
so gilt:
Affine Abbildung
Eine allgemeine affine
Abbildung, die den Punkt
auf den Punkt
abbildet, kann mit Ortsvektoren wie folgt dargestellt werden:
Hierbei ist
der Ortsvektor von
,
der Ortsvektor von
,
eine lineare Abbildung und
ein Vektor, der eine Verschiebung beschreibt. In kartesischen Koordinaten kann
die lineare Abbildung
durch eine Matrix
dargestellt werden und es gilt:
Im dreidimensionalen Raum ergibt dies:
Entsprechende Darstellungen gibt es auch für andere Dimensionen.
Parameterdarstellung einer Geraden
Die Gerade durch die Punkte
und
enthält genau die Punkte
,
deren Ortsvektor
die Darstellung
mit
besitzt. Man spricht hier auch von der Parameterform einer Geradengleichung.
Normalenform der Ebenengleichung
Die Ebene durch den Punkt
(Stützpunkt) mit Normalenvektor
enthält genau die Punkte
,
deren Ortsvektor
die Normalengleichung
erfüllt. Dabei ist
der Ortsvektor (Stützvektor)
des Stützpunkts
und der Malpunkt bezeichnet das Skalarprodukt.
Ortsvektor in verschiedenen Koordinatensystemen
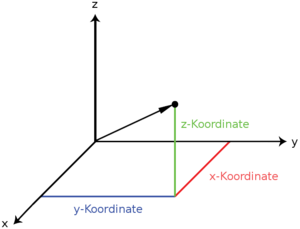
Der durch einen Ortsvektor beschriebene Punkt kann durch die Koordinaten eines Koordinatensystems ausgedrückt werden, wobei der Bezugspunkt des Ortsvektors normalerweise in den Koordinatenursprung gelegt wird.
Kartesische Koordinaten
Üblicherweise wird der Ortsvektor in kartesischen Koordinaten in der Form
definiert. Daher sind die kartesischen Koordinaten gleichzeitig die Komponenten des Ortsvektors.
Zylinderkoordinaten
Der Ortsvektor als Funktion von Zylinderkoordinaten ergibt sich durch Umrechnen der Zylinderkoordinaten in die entsprechenden kartesischen Koordinaten zu
Hier bezeichnet
den Abstand des Punktes von der
-Achse,
der Winkel
wird von der
-Achse
in Richtung der
-Achse
gezählt.
und
sind also die Polarkoordinaten des orthogonal auf die
-
-Ebene
projizierten Punktes.
Mathematisch gesehen wird hier die Abbildung
(Funktion) betrachtet, die den Zylinderkoordinaten
die kartesischen Koordinaten
des Ortsvektors zuordnet.
Kugelkoordinaten
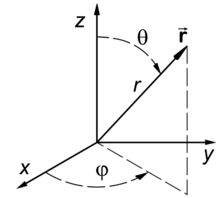
Der Ortsvektor als Funktion von Kugelkoordinaten ergibt sich durch Umrechnen der Kugelkoordinaten in die entsprechenden kartesischen Koordinaten zu
Hierbei bezeichnet
den Abstand des Punktes vom Ursprung (also die Länge des Ortsvektors), der
Winkel
wird in der
-
-Ebene
von der
-Achse
aus in Richtung der
-Achse
gemessen, der Winkel
ist der Winkel zwischen der
-Achse
und dem Ortsvektor.
Physik
Himmelsmechanik
Um die Position eines Himmelskörpers, der sich auf einer Umlaufbahn um ein Schwerezentrum bewegt, anzugeben, wird in der Himmelsmechanik als Ursprung des Orts- oder Radiusvektors dieses Schwerezentrum gewählt. Der Radiusvektor liegt dann stets in Richtung der Gravitationslinie. Die Strecke des Ortsvektors wird Fahrstrahl genannt. Der Fahrstrahl spielt eine zentrale Rolle beim zweiten Keplerschen Gesetz (Flächensatz).
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.02. 2021