Geradengleichung

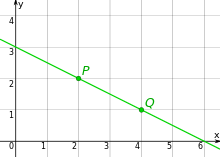
Gerade durch die beiden Punkte und in einem kartesischen Koordinatensystem

Eine Geradengleichung ist eine Gleichung in der Mathematik, die eine Gerade eindeutig beschreibt. Die Gerade besteht aus all den Punkten, deren Koordinaten die Gleichung erfüllen.

Die Abbildung zeigt eine Gerade durch zwei gegebene Punkte und in einem kartesischen Koordinatensystem. Durch zwei voneinander verschiedene Punkte existiert in der euklidischen Geometrie immer genau eine Gerade.

Geraden in der Ebene

Koordinatengleichungen

In einem kartesischen Koordinatensystem werden jedem Punkt der Ebene zwei Zahlen und als Koordinaten zugeordnet. Man schreibt P(x|y) oder P=(x,y) . Eine Gleichung mit den Variablen und beschreibt dann eine Menge von Punkten in der Ebene und zwar die Menge aller Punkte, deren - und -Koordinate die Gleichung erfüllen. Die Schreibweise

$g\colon \ y = 2 x$

bedeutet beispielsweise, dass die Gerade aus allen Punkten (x,y) besteht, die die Gleichung y = 2 x erfüllen. Die entsprechende Mengenschreibweise lautet

$g = \{(x,y) \mid y = 2 x\}$ .

Geraden sind nun dadurch ausgezeichnet, dass es sich bei der zugehörigen Geradengleichung um eine lineare Gleichung handelt. Für solche Gleichungen gibt es eine Reihe unterschiedlicher Darstellungsformen.

Haupt- oder Normalform

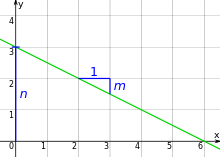
Gerade mit Steigung m und y-Achsenabschnitt n

→ Hauptartikel: Lineare Funktion

Jede Gerade, die nicht parallel zur y-Achse ist, ist der Graph einer linearen Funktion

$f(x) = m \cdot x + n$ ,

wobei und reelle Zahlen sind.^[1] Die zugehörige Geradengleichung lautet dann

$y = m \cdot x + n$ .

Die Parameter und der Geradengleichung haben eine geometrische Bedeutung. Die Zahl ist die Steigung der Geraden und entspricht der senkrechten Kathete des Steigungsdreiecks, dessen waagrechte Kathete die Länge aufweist. Die Zahl ist der y-Achsenabschnitt, das heißt die Gerade schneidet die y-Achse im Punkt (0,n) . Ist n = 0 , so verläuft die Gerade als Ursprungsgerade durch den Koordinatenursprung und die zugehörige Funktion ist dann eine Proportionalität. Die Gerade mit der Gleichung $y = m \cdot x + n$ erhält man aus der Geraden mit der Gleichung $y=m\cdot x$ , indem sie um in Richtung der y-Achse verschoben wird. Diese Verschiebung erfolgt nach oben, wenn positiv ist, und nach unten, wenn negativ ist.

Geraden, die parallel zur y-Achse verlaufen, sind keine Funktionsgraphen. Sie lassen sich durch eine Gleichung der Form

darstellen, wobei eine reelle Zahl ist. Eine solche Gerade schneidet die x-Achse im Punkt (a,0) .

Zweipunkteform

Steigungsdreiecke einer Geraden

→ Hauptartikel: Zweipunkteform

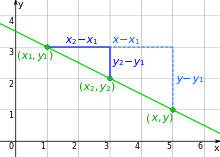
Verläuft die Gerade durch die beiden Punkte (x_1,y_1) und (x_2,y_2) , wobei $x_{1}$ und $x_{2}$ verschieden seien, dann kann die Steigung der Geraden mit Hilfe des Differenzenquotienten durch

$m = \frac{y_2 - y_1}{x_2 - x_1}$

berechnet werden. Nach dem Strahlensatz kann nun statt des Punktes (x_2,y_2) auch ein beliebiger anderer Punkt (x,y) der Geraden gewählt werden, ohne dass die Steigung sich verändert. Damit ergibt sich die Zweipunkteform

$\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$

oder äquivalent dazu, indem die Gleichung nach aufgelöst wird,

$y = \frac{y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) + y_1$

und somit

$y=\underbrace {\left({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\right)} _{m}x+\underbrace {\frac {y_{1}x_{2}-y_{2}x_{1}}{x_{2}-x_{1}}} _{n}$ .

Punktsteigungsform

Punktsteigungsform einer Geradengleichung

→ Hauptartikel: Punktsteigungsform

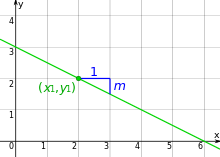
Eine Gerade durch den Punkt (x_1,y_1) mit der Steigung wird durch folgende Gleichung beschrieben:

$y - y_1 = m \cdot (x - x_1)$ .

Diese Formel kann auch benutzt werden, wenn zwei Punkte bekannt sind, aber man den Schnittpunkt mit der y-Achse (oben genannt) nicht explizit bestimmen will.

Koordinatenform

→ Hauptartikel: Koordinatenform

Die Koordinatenform der Geradengleichung in der Ebene lautet

wobei und nicht beide 0 sein dürfen.

Durch Auflösen der Gleichung nach (falls $b \neq 0$ ) erhält man hieraus die explizite Form. Die Koordinatenform hat den Vorteil, dass sie symmetrisch in und ist. Es wird also keine Richtung der Geraden bevorzugt. Geraden, die parallel zur y-Achse sind, spielen keine Sonderrolle.

Achsenabschnittsform

Achsenabschnittsform einer Geradengleichung

→ Hauptartikel: Achsenabschnittsform

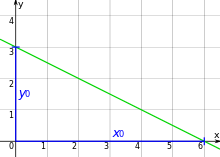
Eine spezielle Form der Koordinatenform ist die Achsenabschnittsform. Schneidet die Gerade die x-Achse im Punkt (x_0,0) und die y-Achse im Punkt (0,y_0) , wobei $x_{0}$ und $y_{0}$ nicht null seien, so lässt sich die Geradengleichung in der Form

$\frac{x}{x_0} + \frac{y}{y_0} = 1$

schreiben. Diese Form heißt Achsenabschnittsform der Geradengleichung mit dem x-Achsenabschnitt $x_{0}$ und dem y-Achsenabschnitt $y_{0}$ . Wird die Gleichung nach aufgelöst, so ergibt sich die explizite Form

$y = -\frac{y_0}{x_0} \cdot x + y_0$ ,

wobei das Verhältnis $-\tfrac{y_0}{x_0}$ gerade der Steigung der Geraden entspricht.

Vektorgleichungen

Es gibt auch die Möglichkeit, eine Gerade mit Hilfe der Vektorrechnung zu beschreiben. Dabei betrachtet man statt der Punkte ihre Ortsvektoren. Der Ortsvektor $\overrightarrow{OP}$ eines Punktes P=(p_1,p_2) wird üblicherweise mit $\vec p = \tbinom{p_1}{p_2}$ bezeichnet.

Parameterform

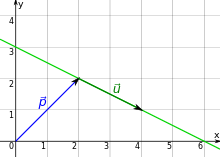
Parameterform einer Geradengleichung

→ Hauptartikel: Parameterform

Bei der Parameterform wird keine Bedingung formuliert, die die Koordinaten der Punkte erfüllen müssen, damit sie auf der Geraden liegen, sondern die Punkte der Geraden werden in Abhängigkeit von einem Parameter dargestellt. Jedem Wert des Parameters entspricht dabei ein Punkt der Geraden. Durchläuft der Parameter alle reellen Zahlen, so erhält man alle Punkte der Geraden. In der Parameterform hat eine Gerade die Darstellung

$\vec x = \vec p + s \, \vec u$

beziehungsweise ausgeschrieben

${x_1 \choose x_2} = {p_1 \choose p_2} + s \, {u_1 \choose u_2}$ .

Hierbei ist ${\vec {p}}$ der Ortsvektor eines festen Punktes der Geraden, ${\vec {u}}$ der Richtungsvektor der Geraden und eine Zahl, die angibt, wie lange in diese Richtung gezählt wird. Der Parameter bildet hierbei die Koordinate eines affinen Koordinatensystems auf der Geraden, das heißt die Gerade wird mit den Werten von beziffert, wobei der Nullpunkt bei (p_1,p_2) liegt.

Normalenform

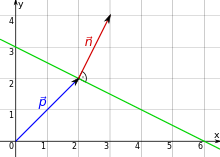
Normalenform einer Geradengleichung

→ Hauptartikel: Normalenform

Mit einem Normalenvektor ${\vec {n}}$ , der im rechten Winkel zur Geraden steht, lässt sich die Gerade in Normalenform schreiben:

$\vec n \cdot (\vec x -\vec p) = 0$ .

Darin ist ${\vec {p}}$ wieder der Ortsvektor eines Geradenpunkts und $\cdot$ das Skalarprodukt zweier Vektoren. Ist $\tbinom{u_1}{u_2}$ ein Richtungsvektor einer Geraden, so ist $\tbinom{-u_2}{u_1}$ ein Normalenvektor der Geraden. Bei der hesseschen Normalform

${\vec n}_0 \cdot \vec x = d$

wird eine Gerade durch einen normierten und orientierten Normalenvektor ${\vec n}_0$ und den Abstand vom Koordinatenursprung beschrieben.

Geraden im Raum

Darstellung einer Raumgeraden

Geraden im Raum lassen sich nicht in der Normalenform darstellen, da sie weder Achsenabschnitte noch einen eindeutig bestimmten Normalenvektor besitzen (zu einer Geraden im Raum gibt es unendlich viele auf ihr senkrecht stehende Richtungen). Gebräuchlich ist die oben vorgestellte Parameterform

$\vec x = \vec p + s \, \vec u$ ,

wobei ${\vec {x}}$ , ${\vec {p}}$ und ${\vec {u}}$ nun Vektoren im Raum sind. Mit Hilfe des Vektorprodukts lässt sich noch eine andere, parameterfreie Geradenform konstruieren, die Determinantenform

$\vec u \times \vec x - \vec u \times \vec p = \vec 0$ .

Hierbei ist ${\vec {p}}$ wiederum der Ortsvektor eines festen Punkts der Geraden und ${\vec {u}}$ der Richtungsvektor der Geraden. Da die Differenz $\vec x - \vec p$ des Ortsvektors ${\vec {x}}$ jedes beliebigen Punktes der Geraden und dem Stützvektor ${\vec {p}}$ kollinear zum Richtungsvektor ${\vec {u}}$ sein muss (also in dieselbe oder in die entgegengesetzte Richtung zeigt), ergibt das Vektorprodukt der beiden immer den Nullvektor:

$\vec u \times (\vec x - \vec p) = \vec 0$ .

Für jeden Vektor ${\vec {x}}$ , der Ortsvektor eines Punktes der Geraden ist, trifft die Gleichung zu, in allen anderen Fällen ergibt sich nicht der Nullvektor. Ist ${\vec {u}}$ ein Einheitsvektor, so entspricht

$|\vec u \times \vec p|$

genau dem Abstand der Geraden vom Ursprung.

Siehe auch

Ebenengleichung

Literatur

Ilja Nikolajewitsch Bronstein, Konstantin Adolfowitsch Semendjajew: Taschenbuch der Mathematik. Harri Deutsch Verlag, 24. Auflage 1989, ISBN 3-87144-492-8.

Anmerkungen

↑ Der Parameter wird in der Literatur auch mit , oder bezeichnet. In Österreich schreibt man meist $f(x) = k \cdot x + d$ .

Basierend auf einem Artikel in:

Wikipedia.de