Euklidische Geometrie
Die euklidische Geometrie ist zunächst die uns vertraute, anschauliche Geometrie des Zwei- oder Dreidimensionalen. Der Begriff hat jedoch sehr verschiedene Aspekte und lässt Verallgemeinerungen zu. Benannt ist dieses mathematische Teilgebiet der Geometrie nach dem griechischen Mathematiker Euklid von Alexandria.
Die Geometrie des Euklid
Im engsten Sinne ist euklidische Geometrie die Geometrie, die Euklid in Die Elemente dargelegt hat.

Über zweitausend Jahre lang wurde Geometrie nach diesem axiomatischen Aufbau gelehrt. Die Redewendung „more geometrico“ (lateinisch: „auf die Art der (euklidischen) Geometrie“) dient noch heute als Hinweis auf eine streng deduktive Argumentation.
Euklid geht dabei folgendermaßen vor:
Definitionen
Das Buch beginnt mit einigen Definitionen, beispielsweise:
- Ein Punkt ist, was keine Teile hat.
- Eine Linie ist eine breitenlose Länge.
- Eine Gerade ist eine Linie, die bezüglich der Punkte auf ihr stets gleich liegt.
Ähnlich werden Ebene, Winkel u.a. definiert.
Außer diesen mehr oder weniger anschaulichen Definitionen von Grundbegriffen gibt es auch Definitionen, die im modernen Sinne als Worteinführungen zu verstehen sind, weil sie im folgenden Text abkürzend gebraucht werden, so zum Beispiel für Parallelen: „Parallel sind gerade Linien, die in derselben Ebene liegen und dabei, wenn man sie nach beiden Seiten ins Unendliche verlängert, auf keiner Seite einander treffen.“
Insgesamt geben die Elemente 35 Definitionen.
Postulate
Nach den eher beschreibenden Definitionen folgen die fünf eher festlegenden Postulate. Gefordert wird hier,
- dass man von jedem Punkt nach jedem Punkt die Strecke ziehen könne,
- dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern könne,
- dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen könne,
- dass alle rechten Winkel einander gleich seien,
- dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirke, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte würden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen würden auf der Seite, auf der die Winkel lägen, die zusammen kleiner als zwei rechte seien (kurz: dass zu einer geraden Linie durch einen gegebenen Punkt, der außerhalb dieser Geraden läge, höchstens eine dazu parallele gerade Linie existieren dürfe, siehe Parallelenpostulat).
Euklids Axiome
An die fünf aufgeführten geometrischen Postulate schließen sich mehrere logische Axiome an, zum Beispiel:
- Was demselben gleich ist, ist auch einander gleich.
- Wenn Gleichem Gleiches hinzugefügt wird, sind die Ganzen gleich.
- Wenn von Gleichem Gleiches weggenommen wird, sind die Reste gleich.
Probleme und Theoreme
Hierauf aufbauend behandelt Euklid nun Probleme …
- Beispiel: „Über einer gegebenen Strecke ein gleichseitiges Dreieck errichten.“
… und Theoreme
- Beispiel: „Wenn in einem Dreieck zwei Winkel einander gleich sind, müssen auch die den gleichen Winkeln gegenüberliegenden Seiten einander gleich sein.“
Zur Lösung eines Problems oder zum Beweis eines Theorems werden grundsätzlich nur die Definitionen, Postulate und Axiome sowie vorher bewiesene Theoreme und die Konstruktionen aus vorher gelösten Problemen verwendet.
Geometrie und Wirklichkeit bei Euklid
Als Platoniker war Euklid davon überzeugt, dass die von ihm formulierten Postulate und Axiome die Wirklichkeit wiedergeben. Gemäß Platons Ideenlehre gehören sie einer ontologisch höherrangigen Ebene an als die in den Sand gezeichneten Figuren, die ihre Abbildungen sind. Das Verhältnis zwischen einem unvollkommen gezeichneten Kreis und der vollkommenen Idee des Kreises illustriert den Unterschied zwischen der sinnlich wahrnehmbaren Welt und der intelligiblen (nur geistig erfassbaren) Welt, der in Platons Höhlengleichnis veranschaulicht wird.
Unterschiede zu einer rein axiomatischen Theorie
Aus heutiger Sicht genügen Die Elemente nicht dem Anspruch an eine axiomatische Theorie:
- Zweck der Definitionen (soweit sie Grundbegriffe betreffen) ist es bei Euklid, den Bezug zur vertrauten geometrischen Erfahrungswelt herzustellen und die Postulate zu motivieren. Die Aussagekraft solcher Sätze wird sehr unterschiedlich beurteilt. Strenge Axiomatiker halten sie für überflüssig.
- Die fünf Postulate repräsentieren am ehesten das, was heute als Axiom angesehen würde. Als Grundlage für die aus ihnen gezogenen Schlüsse sind sie aber nicht umfassend genug und zu ungenau. – Anzumerken ist, dass zumindest die drei ersten „Postulate“ die Möglichkeit von bestimmten Konstruktionen postulieren (und nicht etwa das Zutreffen bestimmter Sachverhalte). Euklids Axiomatik kann deshalb auch als konstruktive Axiomatik bezeichnet werden.
- Die als Axiome bezeichneten Aussagen betreffen weniger die Geometrie als vielmehr die logischen Grundlagen. Im Sinne einer Begründung der Logik sind sie allerdings lückenhaft.
Hieraus folgt, dass die Schlüsse notgedrungen eine Vielzahl von unausgesprochenen Annahmen verwenden.
Die moderne axiomatische Theorie
In einem anderen Sinne ist euklidische Geometrie eine am Ende des 19. Jahrhunderts entstandene, streng axiomatische Theorie. Die oben genannten Probleme wurden deutlich, als sich Russell, Hilbert und andere Mathematiker um eine strengere Grundlegung der Mathematik bemühten.
Sie wurden gelöst von David Hilbert in seinem Werk Grundlagen der Geometrie (Teubner 1899, zahlreiche Neuauflagen). Vorläufer waren Hermann Graßmann, Moritz Pasch, Giuseppe Peano und andere. Auch nach Hilbert wurden mehrere andere Axiomensysteme für die euklidische Geometrie aufgestellt.
Hilberts Vorgehensweise
David Hilbert verwendet „drei verschiedene Systeme von Dingen“, nämlich Punkte, Geraden und Ebenen, von denen er nur sagt: „Wir denken (sie) uns“. Diese Dinge sollen „in drei grundlegenden Beziehungen“ zueinander „gedacht werden“, nämlich „liegen“, „zwischen“ und „kongruent“. Zur Verknüpfung dieser „Dinge“ und „Beziehungen“ stellt er dann 20 Axiome in fünf Gruppen auf:
- Acht Axiome der Verknüpfung (Inzidenz)
- Vier Axiome der Anordnung (Ordnung)
- Fünf Axiome der Kongruenz (Kongruenz)
- Das Axiom der Parallelen (Parallelenaxiom)
- Zwei Axiome der Stetigkeit (archimedisches Axiom und Vollständigkeitsaxiom)
Geometrie und Wirklichkeit bei Hilbert
Als ein Vertreter des Formalismus erklärt Hilbert es für irrelevant, was diese Punkte, Geraden und Ebenen mit der Wirklichkeit zu tun haben. Die Bedeutung der Grundbegriffe sei dadurch bestimmt, dass sie die Axiome erfüllen. So beginnt er den Abschnitt über die Axiome der Verknüpfung mit dem Satz: „Die Axiome dieser Gruppe stellen zwischen den oben eingeführten Dingen: Punkte, Geraden und Ebenen eine Verknüpfung her und lauten wie folgt:…“ Die Definitionen der Grundbegriffe erfolgen also implizit.
Andererseits erklärt Hilbert in der Einleitung zu seinem Werk: „Die vorliegende Untersuchung ist ein neuer Versuch, für die Geometrie ein vollständiges und möglichst einfaches System von Axiomen aufzustellen…“. Mit diesem Bezug auf die Geometrie stellt er klar, dass es ihm nicht um einen beliebigen Formalismus geht, sondern um eine Präzisierung dessen, was Euklid mit „Geometrie“ gemeint hat und was wir alle als die Eigenschaften des uns umgebenden Raumes kennen. – Diese Präzisierung ist Hilbert vollständig gelungen, und sie erweist sich als viel aufwändiger, als Euklid ahnte.
Weitere Axiomensysteme
Später aufgestellte Axiomensysteme sind grundsätzlich äquivalent zu dem Hilberts. Sie berücksichtigen die Weiterentwicklung der Mathematik.
Eine mögliche Axiomatisierung ist gegeben durch die Axiome der absoluten Geometrie zusammen mit dem folgenden Axiom, das unter Voraussetzung der übrigen Axiome der absoluten Geometrie gleichwertig zum Parallelenaxiom ist:
- Zu jeder Geraden existiert eine von ihr verschiedene Parallele. Sind zwei Geraden zu einer dritten parallel, dann sind sie auch parallel zueinander.
Euklidische und nichteuklidische Geometrie
Weiterhin dient der Begriff euklidische Geometrie als Gegenbegriff zu den nichteuklidischen Geometrien
Den Impuls gab dabei die Auseinandersetzung mit dem Parallelenpostulat. Nachdem jahrhundertelang zuvor vergeblich versucht worden war, dieses fünfte Postulat des Euklid auf ein einfacheres zurückzuführen, schlussfolgerten der Ungar János Bolyai und der Russe Nikolai Iwanowitsch Lobatschewski um 1830, dass eine Verneinung dieses fünften Postulates zu logischen Widersprüchen führen müsse, wenn dieses tatsächlich auf einfachere Aussagen zurückgeführt werden könne. Also verneinten die beiden Mathematiker dieses Postulat und definierten jeweils eigene (Ersatz-)Postulate, die wider Erwarten zu einem logisch völlig einwandfreien geometrischen System führten – den nichteuklidischen Geometrien: „Nicht der Beweis war indes so beunruhigend, sondern vielmehr sein rationales Nebenprodukt, das schon bald ihn und fast alles in der Mathematik überschatten sollte: Die Mathematik, der Eckstein wissenschaftlicher Gewissheit, war auf einmal ungewiss geworden. Man hatte es jetzt mit zwei einander widersprechenden Visionen unantastbarer wissenschaftlicher Wahrheit zu tun“, was zu einer tiefen Krise in den Wissenschaften führte (Pirsig, 1973).
Die genaue Formulierung des „hyperbolischen“ Axioms, das in der Geometrie von Lobatschewski, der hyperbolischen Geometrie, an die Stelle des Parallelenaxioms tritt, lautet: „... durch einen auf einer Gerade nichtliegenden Punkt gehen mindestens zwei Geraden, die mit dieser in einer Ebene liegen und sie nicht schneiden ...“
Nichteuklidische Geometrien und die Wirklichkeit
Ob nichteuklidische Geometrien (es gibt verschiedene) den realen Raum beschreiben können, wird unterschiedlich beantwortet. Meist werden sie als rein abstrakt-mathematische Theorien verstanden, die nur durch die Ähnlichkeit der Begriffe und Axiomensysteme den Namen „Geometrie“ verdienen.
Diese Theorien haben sich inzwischen allerdings in der theoretischen Physik als sehr relevant für die Beschreibung der Realität unseres Weltalls erwiesen.
Die analytische Geometrie der Ebene und des Raumes
In einem Koordinatensystem
lässt sich ein Punkt darstellen als ein Paar
(in der ebenen Geometrie) oder als ein Tripel
von reellen Zahlen. Eine Gerade
oder Ebene ist dann eine Menge von solchen Zahlenpaaren (bzw. -tripeln), deren
Koordinaten eine lineare Gleichung erfüllen. Die hierauf aufgebaute
analytische Geometrie der reellen
Zahlenebene
oder des reellen Zahlenraums
erweist sich als völlig äquivalent zu der axiomatisch definierten.
Man kann die analytische Geometrie als ein Modell für die axiomatische Theorie ansehen. Dann liefert sie einen Beweis der Widerspruchsfreiheit des Axiomensystems (wobei man allerdings eine widerspruchsfreie Begründung der reellen Zahlen als gegeben voraussetzen muss).
Man kann den analytischen Zugang aber auch als eine selbstständige (und bequemere) Begründung der Geometrie ansehen; aus dieser Sicht ist der axiomatische Zugang nur noch von geschichtlichem Interesse. Bourbaki zum Beispiel (und ebenso Jean Dieudonné) verzichtet vollständig auf die Verwendung originär geometrischer Begriffe und hält mit der Behandlung der topologischen Vektorräume das Thema für erledigt.
Euklidische Geometrie als Lehre vom Messen
Euklidische Geometrie ist auch die Geometrie, in der Strecken und Winkeln Maße zugeordnet werden.
Im axiomatischen Aufbau der euklidischen Geometrie kommen Zahlen scheinbar überhaupt nicht vor. Es ist allerdings festgelegt, wie man an eine Strecke eine kongruente in der gleichen Richtung anfügt, diese also verdoppelt - und folglich auch mit einer beliebigen natürlichen Zahl vervielfacht. Es gibt auch eine Konstruktion, um eine gegebene Strecke in n gleiche Teile zu teilen. Wird nun noch eine beliebige Strecke als Einheitsstrecke ausgezeichnet, so ist es damit möglich, Strecken zu konstruieren, deren Maßzahl eine beliebige rationale Zahl ist. Dies ist der wesentliche Gegenstand der altgriechischen Arithmetik.
Bei anderen Konstruktionen ergeben sich Strecken, die keine rationale Zahl als Maßzahl haben. (Etwa die Diagonale des Quadrats über der Einheitsstrecke oder ihre Abschnitte bei der Teilung nach dem goldenen Schnitt.) Dies nachgewiesen zu haben, zeugt von dem unglaublich hohen Niveau der griechischen Mathematik schon zur Zeit der Pythagoreer. Somit wird die Einführung von irrationalen Zahlen erforderlich. 2000 Jahre später stellt Hilberts Vollständigkeitsaxiom sicher, dass alle reellen Zahlen als Maßzahlen für Strecken auftreten können.
Die Festlegung von Maßzahlen für Winkel verläuft ähnlich. Die Festlegung
eines „Einheitswinkels“ entfällt, da mit dem Vollwinkel (oder dem
Rechten Winkel) ein objektives Maß existiert. Andererseits ist die Teilung des Winkels
in 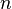 gleiche Teile wesentlich problematischer; längst nicht zu jedem rationalen
Winkelmaß lässt sich ein Winkel konstruieren.
Schon die Dreiteilung des Winkels misslingt im Allgemeinen.
gleiche Teile wesentlich problematischer; längst nicht zu jedem rationalen
Winkelmaß lässt sich ein Winkel konstruieren.
Schon die Dreiteilung des Winkels misslingt im Allgemeinen.
Die so eingeführte Metrik
ist äquivalent zu der durch die euklidische
Norm induzierten euklidische
Metrik des „analytischen“
oder
.
Für die durch ihre Koordinaten gegebenen Punkte
und
ist also
.
Maßzahlen für Winkel lassen sich in der analytischen Geometrie über das Skalarprodukt von Vektoren definieren.
Verallgemeinerung für höhere Dimensionen
Als analytische Geometrie lässt sich die euklidische Geometrie ohne weiteres für eine beliebige (auch unendliche) Anzahl von Dimensionen verallgemeinern.
Zu den Geraden und Ebenen treten dann höherdimensionale lineare Punktmengen,
die als Hyperebenen bezeichnet werden. (In einem engeren Sinne ist eine Hyperebene
eines -dimensionalen
Raumes ein möglichst „großer“, also
-dimensionaler
Teilraum.)
Die Zahl der Dimensionen ist dabei nicht beschränkt und muss auch nicht endlich sein. Zu jeder Kardinalzahl lässt sich ein euklidischer Raum dieser Dimension definieren.
Räume mit mehr als drei Dimensionen sind für unser Vorstellungsvermögen grundsätzlich unzugänglich. Sie wurden auch nicht mit dem Anspruch entworfen, menschliche Raumerfahrung darzustellen. Ähnlich wie bei den nichteuklidischen Geometrien fanden sich aber auch hier Bezüge zur theoretischen Physik: Die Raumzeit der speziellen Relativitätstheorie lässt sich als vierdimensionaler Raum darstellen. In der modernen Kosmologie gibt es Erklärungsansätze mit noch erheblich mehr Dimensionen.
Verwandte Gebiete
Verzichtet man auf das 3. und 4. euklidische Postulat (also auf die Begriffe „Kreis“ und „Rechter Winkel“) oder beschränkt man sich, für eine präzisere Definition, auf Hilberts Axiome der Verknüpfung und der Parallelen, so erhält man eine affine Geometrie. Sie wurde von Leonhard Euler erstmals entwickelt. Die Begriffe „Abstand“ und „Winkelmaß“ kommen hier nicht vor, wohl aber Streckenverhältnisse und Parallelität.
Ersetzt man das Parallelenaxiom durch die Festsetzung, dass zwei in einer Ebene gelegene Geraden immer einen Schnittpunkt haben sollen, so entsteht aus der affinen eine projektive Geometrie.
Wenn die Anordnungs- und Stetigkeitsaxiome wegfallen, können affine und projektive Geometrien auch aus endlich vielen Punkten bestehen.
In der synthetischen Geometrie wird der Begriff einer euklidischen Ebene so verallgemeinert, dass genau die Ebenen, deren affine Koordinaten in einem euklidischen Körper liegen, euklidische Ebenen sind.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.06. 2020