Bose-Einstein-Statistik
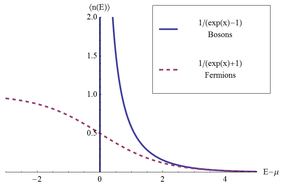
für Bosonen (Bose-Einstein-Statistik, obere Kurve)
bzw. Fermionen (Fermi-Dirac-Statistik, untere Kurve),
jeweils im Spezialfall der Wechselwirkungsfreiheit und bei konstanter Temperatur
Das chemische Potential
im Bose-Fall ist es immer kleiner als die Energie und würde im Grenzfall der Bose-Einstein-Kondensation verschwinden;
im Fermi-Fall dagegen ist es positiv, bei
Die Bose-Einstein-Statistik oder auch Bose-Einstein-Verteilung,
benannt nach Satyendranath Bose (1894–1974) und Albert Einstein (1879–1955), ist eine Wahrscheinlichkeitsverteilung
in der Quantenstatistik
(dort auch die Herleitung). Sie beschreibt die mittlere Besetzungszahl
eines Quantenzustands
der Energie
im thermodynamischen
Gleichgewicht bei der absoluten
Temperatur
für identische
Bosonen als
besetzende Teilchen.
Analog existiert für Fermionen
die Fermi-Dirac-Statistik,
die ebenso wie die Bose-Einstein-Statistik im Grenzfall großer Energie
in die Boltzmann-Statistik
übergeht.
Kernpunkt der Bose-Einstein-Statistik ist, dass bei gleichzeitiger
Vertauschung aller vier Variablen
zweier Bosonen (
und
:
Ortsvariable;
:
Spinvariable) die
Wellenfunktion
bzw. der Zustandsvektor
eines Vielteilchensystems
nicht das Vorzeichen
wechselt
,
während es in der Fermi-Dirac-Statistik sehr wohl wechselt
.
Im Gegensatz zu Fermionen können deshalb mehrere Bosonen im gleichen
Ein-Teilchen-Zustand sein, also die gleichen Quantenzahlen
haben.
Bei Wechselwirkungsfreiheit
Bei Wechselwirkungsfreiheit (Bosegas) ergibt sich für Bosonen die folgende Formel:
mit
- dem chemischen
Potential
, welches für Bosonen stets kleiner als der niedrigste mögliche Energiewert ist:
;
daher ist die Bose-Einstein-Statistik nur für Energiewertedefiniert.
- der Energienormierung
. Die Wahl von
hängt von der verwendeten Temperaturskala ab:
- üblicherweise wird sie gewählt zu
mit der Boltzmann-Konstanten
;
- sie beträgt
, wenn die Temperatur in Energieeinheiten, etwa Joule, gemessen wird; dies geschieht, wenn
auch in der Definition der Entropie – welche dann einheitenlos ist – nicht auftaucht.
- üblicherweise wird sie gewählt zu
Unterhalb einer sehr tiefen kritischen Temperatur
erhält man bei Wechselwirkungsfreiheit – unter der Annahme, dass
gegen das Energie-Minimum strebt – die Bose-Einstein-Kondensation.
Man beachte, dass es sich bei
um die Besetzungszahl eines Quantenzustandes handelt. Benötigt man die
Besetzungszahl eines entarteten
Energieniveaus, so ist
obiger Ausdruck zusätzlich mit dem entsprechenden Entartungsgrad
zu multiplizieren (
:
Spin, bei Bosonen immer ganzzahlig), vgl. auch Multiplizität.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.07. 2020