Quotientenkriterium

Das Quotientenkriterium ist ein mathematisches Konvergenzkriterium für Reihen. Es basiert auf dem Majorantenkriterium, das heißt, eine komplizierte Reihe wird durch eine einfache, hier die geometrische Reihe, nach oben abgeschätzt. Die geometrische Reihe konvergiert genau dann, wenn der Betrag der Folgenglieder abnimmt, also der (konstante) Quotient zweier aufeinanderfolgender Glieder kleiner als 1 ist. Nimmt eine andere Reihe ab einem bestimmten Element mindestens genauso schnell ab, ist also der Quotient kleiner oder gleich , so ist auch diese konvergent. Mit dem Quotientenkriterium kann auch Divergenz nachgewiesen werden. Bleibt der Quotient immer größer oder gleich 1, wird der Betrag der Folgenglieder nicht kleiner. Da diese dann keine Nullfolge bilden, ist die Reihe divergent.

Entwickelt wurde das Quotientenkriterium von dem Mathematiker und Physiker Jean-Baptiste le Rond d’Alembert, zu dessen Ehren diese mathematische Aussage auch d’Alembertsches Konvergenzkriterium genannt wird.

Aussage

Entscheidungsbaum für das Quotientenkriterium

Gegeben sei eine Reihe $S := \sum_{n=0}^\infty a_n$ mit reellen oder komplexen Summanden, $a_n\neq 0$ für fast alle $n\in \mathbb {N}$ . Gibt es ein q < 1 , so dass für fast alle $n\in \mathbb {N}$ gilt

$\left|\frac{a_{n+1}}{a_n}\right| \le q<1,$

so ist die Reihe absolut konvergent. Gilt dagegen für fast alle $n\in \mathbb {N}$

$\left|\frac{a_{n+1}}{a_n}\right| \ge 1$ ,

so ist die Reihe divergent.

Im Fall der Konvergenz muss von unabhängig und echt kleiner als 1 sein. Gilt lediglich $\left|\frac{a_{n+1}}{a_n}\right|<1$ , kann also $\left|\frac{a_{n+1}}{a_n}\right|$ beliebig nahe an 1 herankommen, so liefert das Quotientenkriterium keine Aussage über die Konvergenz oder die Divergenz.

Beispiele

Beispiel 1. Wir betrachten die Reihe

$\sum_{n=0}^\infty \frac{5 + n}{10^n}$

und prüfen diese auf Konvergenz. Über das Quotientenkriterium erhalten wir:

$\left| \frac{a_{n+1}}{a_n} \right| = \frac{5 + (n+1)}{10^{n+1}} \cdot \frac{10^n}{5+n} = \frac{1}{10} \cdot \frac{6+n}{5+n} \leq \frac{3}{25} < 1$ .

Folglich ist die Reihe konvergent.

Beispiel 2. Wir betrachten die Reihe

$\sum_{n=1}^\infty \frac{n!}{2^n}$

und prüfen diese auf Konvergenz. Wir erhalten:

$\left|{\frac {a_{n+1}}{a_{n}}}\right|={\frac {(n+1)!}{2^{n+1}}}\cdot {\frac {2^{n}}{n!}}={\frac {n+1}{2}}\geq 1$ .

Somit ist diese Reihe divergent.

Beispiel 3. Wir wollen den Konvergenzradius der Potenzreihe

$\sum_{n=1}^\infty \frac{n!}{n^n} z^n$

für komplexe Zahlen $z \in \mathbb{C}$ bestimmen. Für z = 0 ist die Reihe offensichtlich gegen 0 konvergent, sei also $z \not= 0$ und wir erhalten

$\left|{\frac {a_{n+1}}{a_{n}}}\right|=\left|{\frac {(n+1)!n^{n}}{n!(n+1)^{n+1}}}{\frac {z^{n+1}}{z^{n}}}\right|=\left({\frac {1}{1+{\frac {1}{n}}}}\right)^{n}|z|\,\,{\overset {n\to \infty }{\longrightarrow }}\,\,{\frac {|z|}{e}}$ .

Der Konvergenzradius ist also die eulersche Zahl .

Ein Beispiel für die Nichtanwendbarkeit des Quotientenkriteriums ist die allgemeine harmonische Reihe $\sum _{n=1}^{\infty }{\frac {1}{n^{\alpha }}}$ . Es gilt

$\left|\frac{a_{n+1}}{a_n}\right|=\left(\frac{n}{n+1}\right)^\alpha<1$ .

Für $\alpha =1$ ist die allgemeine harmonische Reihe divergent, für $\alpha >1$ konvergent; das Quotientenkriterium kann aber die beiden Fälle nicht unterscheiden.

Beweisidee

Der Fall der Konvergenz folgt mit dem Majorantenkriterium aus der Konvergenz von $\sum_{n=0}^\infty q^n$ , einer geometrischen Reihe. Das Kriterium für Divergenz folgt daraus, dass die Glieder dann wegen $0<\left|a_n\right|\leq\left|a_{n+1}\right|$ keine Nullfolge bilden können.

Spezialfälle

Existiert $L:=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|$ , so liefert das Quotientenkriterium

für absolute Konvergenz,
für Divergenz,
für keine Konvergenzaussage.

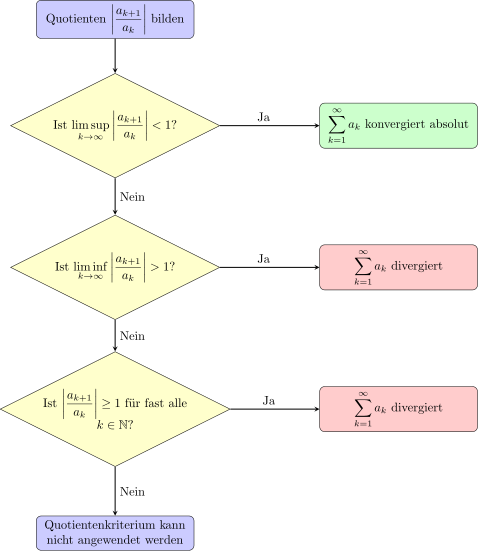
Unter Verwendung von Limes superior und Limes inferior lässt sich das Quotientenkriterium folgendermaßen formulieren:

Ist $\limsup_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|<1$ , so ist die Reihe absolut konvergent,
ist $\liminf_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|>1$ , so ist die Reihe divergent,
ist $\liminf_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|\leq 1\leq \limsup_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|$ , so lässt sich keine Konvergenzaussage machen.

Im Gegensatz zum Wurzelkriterium muss für das Divergenzkriterium nicht der Limes superior, sondern der Limes inferior verwendet werden.

Abgewandeltes Quotientenkriterium

Neben dem „gewöhnlichen“ Quotientenkriterium gibt es noch folgende Versionen (Kriterium von Raabe): Sei $(a_n)_{n\in\mathbb{N}}$ eine Folge mit echt positiven Gliedern. Wenn nun

$\exists d>1,n_0\in\mathbb{N}:\forall n\ge n_0:\frac{a_{n+1}}{a_n}\le 1-\frac{d}{n}$ ,

so gilt, dass $\sum_{n=1}^\infty a_n$ konvergent ist.

Ist andererseits

$\exists n_0:\forall n\ge n_0: \frac{a_{n+1}}{a_n}\ge 1-\frac{1}{n}$ ,

so folgt:

$\sum_{n=1}^\infty a_n$ divergiert gegen $\infty$ .

Anwendungen

Mit dem Quotientenkriterium lässt sich beispielsweise die Konvergenz der Taylorreihen für die Exponentialfunktion und für die Sinus- und Kosinusfunktionen zeigen.

Basierend auf einem Artikel in:

Wikipedia.de