Konvergenzkriterium
In der Analysis ist ein Konvergenzkriterium ein Kriterium, mit dem die Konvergenz einer Folge oder Reihe bewiesen werden kann. Insbesondere sind damit Kriterien für die Konvergenz reeller Folgen oder Reihen gemeint. Mit einigen dieser Kriterien kann auch die Divergenz einer Folge oder Reihe nachgewiesen werden.
Konvergenzkriterien für Folgen
Wichtige Konvergenzkriterien für Folgen sind:
- Monotoniekriterium: Eine monotone Folge reeller Zahlen konvergiert genau dann, wenn sie beschränkt ist.
- Cauchy-Kriterium: Eine Folge reeller oder komplexer Zahlen konvergiert genau dann, wenn sie eine Cauchy-Folge ist.
- Sandwichkriterium: Eine Folge reeller Zahlen konvergiert, wenn sie nach unten und nach oben durch konvergente Folgen abgeschätzt werden kann, die den gleichen Grenzwert haben.
Konvergenzkriterien für Reihen
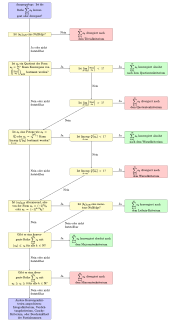
Für Reihen werden drei Arten von Konvergenzkriterien unterschieden:
- Direkte Kriterien, die aus Eigenschaften der Partialsummenfolge der Reihe auf Konvergenz schließen,
- Vergleichskriterien 1. Art, die den Absolutbetrag bzw. die Norm der Reihenglieder mit einer bekannten Reihe vergleichen, und
- Vergleichskriterien 2. Art, die die Quotienten der Absolutbeträge aufeinanderfolgender Glieder mit den entsprechenden Quotienten einer bekannten Reihe vergleichen.
Die folgende Tabelle gibt einen Überblick über bekannte Konvergenzkriterien. Die Kriterien ermöglichen unterschiedliche Aussagen: Einige erlauben nur den Schluss auf Konvergenz, mit anderen kann auch Divergenz bewiesen werden, einige zeigen absolute Konvergenz, andere nur Konvergenz (aus absoluter Konvergenz folgt Konvergenz, aber nicht umgekehrt). Zudem erlauben verschiedene Kriterien eine Abschätzung des Grenzwerts oder eine Fehlerabschätzung.
| Kriterium | nur für monotone Folgen |
Konvergenz | Divergenz | absolute Konvergenz |
Abschätzung | Fehler- abschätzung |
Art |
|---|---|---|---|---|---|---|---|
| Nullfolgenkriterium | x | Direktes Kriterium | |||||
| Monotoniekriterium | x | x | |||||
| Leibniz-Kriterium | x | x | x | x | |||
| Cauchy-Kriterium | x | x | |||||
| Abel-Kriterium | x | x | |||||
| Dirichlet-Kriterium | x | x | |||||
| Majorantenkriterium | x | x | Vergleichskriterium 1. Art | ||||
| Minorantenkriterium | x | ||||||
| Wurzelkriterium | x | x | x | x | |||
| Integralkriterium | x | x | x | x | x | ||
| Cauchy-Verdichtungskriterium | x | x | x | x | |||
| Grenzwertkriterium | x | x | |||||
| Quotientenkriterium | x | x | x | x | Vergleichskriterium 2. Art | ||
| Gauß-Kriterium | x | x | x | ||||
| Raabe-Kriterium | x | x | x | ||||
| Kummer-Kriterium | x | x | x | ||||
| Bertrand-Kriterium | x | x | x | ||||
| Ermakoff-Kriterium | x | x | x | x | |||
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.05. 2021