
Umkreis
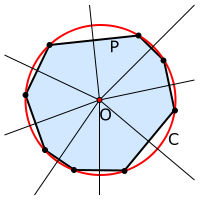
In der ebenen Geometrie ist ein Umkreis ein Kreis, der durch alle Eckpunkte eines Polygons (Vielecks) geht.
Nicht für jedes Polygon existiert ein solcher Umkreis. Allgemein besitzt ein konvexes Polygon genau dann einen Umkreis, wenn die Mittelsenkrechten aller Seiten einander in einem Punkt schneiden. In diesem Fall ist der gemeinsame Punkt der Mittelpunkt des Umkreises.
Umkreis eines Dreiecks
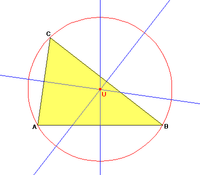
Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
Alle Punkte der Mittelsenkrechten zu
sind von
und
gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu
übereinstimmende Entfernungen von
und
.
Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken
(
,
und
)
gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten
liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des
Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
Der Umkreismittelpunkt, also der Schnittpunkt der Mittelsenkrechten, zählt zu
den ausgezeichneten
Punkten des Dreiecks. Er trägt die Kimberling-Nummer
.
Sonderfälle
Für spitzwinklige Dreiecke liegt der Umkreismittelpunkt im Inneren des Dreiecks. Beim rechtwinkligen Dreieck ist der Mittelpunkt der Hypotenuse zugleich Umkreismittelpunkt (siehe Satz des Thales). Im Falle eines stumpfwinkligen Dreiecks (mit einem Winkel über 90°) befindet sich der Umkreismittelpunkt außerhalb des Dreiecks.
Radius
Der Umkreisradius eines Dreiecks lässt sich mit dem Sinussatz
oder aus der Dreiecksfläche berechnen.
Dabei stehen die Bezeichnungen ,
,
für die Seitenlängen und
,
,
für die Größen der Innenwinkel.
bezeichnet den Flächeninhalt
des Dreiecks, der sich z.B. mit Hilfe der heronischen Formel
berechnen lässt.
Koordinaten
| Umkreismittelpunkt eines
Dreiecks ( | |
|---|---|
| Trilineare Koordinaten | |
| Baryzentrische Koordinaten | |
Weitere Eigenschaften
- Der Umkreismittelpunkt liegt wie der Schwerpunkt und der Höhenschnittpunkt auf der eulerschen Geraden.
- Nach dem Südpolsatz schneidet sich die Mittelsenkrechte einer Dreiecksseite mit der Winkelhalbierenden des gegenüberliegenden Winkels stets auf dem Umkreis.
- Die Entfernung zwischen Umkreismittelpunkt und Inkreismittelpunkt beträgt
, wobei
den Umkreisradius und
den Inkreisradius bezeichnet (Satz von Euler).
- Die Summe der vorzeichenbehafteten Abstände des Umkreismittelpunktes von den Dreiecksseiten ist gleich der Summe aus Umkreis- und Inkreisradius (Satz von Carnot).
Verallgemeinerung: Mittellotensatz
Die Aussage, dass sich die Mittelsenkrechten der Dreiecksseiten in einem Punkt schneiden, wird in der synthetischen Geometrie als Mittellotensatz bezeichnet. Dort kann für allgemeinere affine Ebenen, in denen kein Abstandsbegriff und damit keine "Kreise" definiert sind, gezeigt werden, dass dieser Satz äquivalent zum Höhenschnittpunktsatz ist. → Siehe dazu Höhenschnittpunkt und präeuklidische Ebene.
Umkreise anderer Vielecke
Während beim Dreieck stets ein Umkreis existiert, trifft dies bei Vielecken (Polygonen) mit mehr als drei Ecken nur in besonderen Fällen zu.
Vierecke, die einen Umkreis haben, werden Sehnenvierecke genannt. Spezialfälle sind gleichschenklige Trapeze, also auch Rechtecke und Quadrate.
Unabhängig von der Eckenzahl hat jedes regelmäßige
Polygon einen Umkreis. Für den Umkreisradius eines regelmäßigen -Ecks
mit der Seitenlänge
gilt:
Verwandte Begriffe
Der Inkreis eines Vielecks ist ein Kreis, der alle Seiten dieses Vielecks berührt. Der Inkreis eines Dreiecks stellt einen besonders wichtigen Spezialfall dar. Er gehört mit dem Umkreis und den drei Ankreisen zu den besonderen Kreisen der Dreiecksgeometrie.
Überträgt man die Definition des Umkreises auf den (dreidimensionalen) Raum, so erhält man den Begriff der Umkugel, also einer Kugel, auf der alle Eckpunkte eines gegebenen Polyeders (Vielflächners) liegen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.01. 2022