Baryzentrische Koordinaten

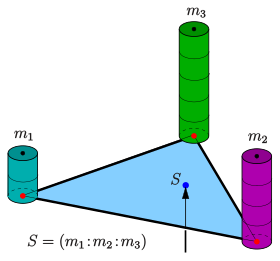
Die baryzentrischen Koordinaten eines Punktes (blau) sind die Verhältnisse dreier Massen in den Ecken eines Dreiecks (rot), deren Schwerpunkt (Massenmittelpunkt) der Punkt ist. In diesem Beispiel hat die baryzentrischen Koordinaten $(2:4:5)$ .

Die Verbindung zwischen Physik und Geometrie liefert die Gleichung des Hebelgesetzes: Danach ist das Verhältnis der Massen $m_{1},m_{2}$ gleich dem Verhältnis der Strecken $l_{2},l_{1}$ , die die Lage des Schwerpunktes beschreiben.

Baryzentrische Koordinaten (auch homogene baryzentrische Koordinaten) dienen in der linearen Algebra und in der Geometrie dazu, die Lage von Punkten in Bezug auf eine gegebene Strecke, ein gegebenes Dreieck, ein gegebenes Tetraeder oder allgemeiner ein gegebenes Simplex zu beschreiben.

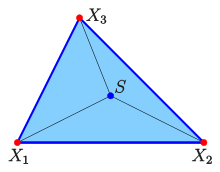
Ebene baryzentrische Koordinaten eines Punktes kann man sich als Verhältnisse von drei Massen $m_{1},m_{2},m_{3}$ vorstellen, die sich in den Ecken eines vorgegebenen Dreiecks befinden und deren Schwerpunkt ist (siehe Bild). Da es dabei nur auf Verhältnisse ankommt, schreibt man $(m_{1}:m_{2}:m_{3})$ . Sind alle Massen gleich, ist der geometrische Schwerpunkt des Dreiecks und hat die baryzentrischen Koordinaten $(1:1:1)$ . 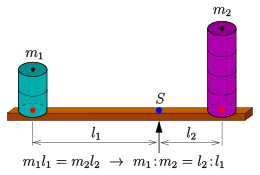Ihre geometrische Bedeutung erhalten die baryzentrischen Koordinaten durch die folgenden Eigenschaften: Im 1-Dimensionalen ist das Massenverhältnis gleich einem Verhältnis von Teilstrecken (siehe 2. Bild), im 2-Dimensionalen sind die Massenverhältnisse gleich Flächenverhältnissen von Teildreiecken.

Baryzentrische Koordinaten wurden zuerst von A. F. Möbius 1827 in seinem Buch Der baryzentrische Calcul eingeführt. Sie sind ein Spezialfall homogener Koordinaten. Ein wesentlicher Unterschied zu den üblichen homogenen Koordinaten, z.B. in der Ebene, ist die Beschreibung der Ferngerade durch die Gleichung $x_{1}+x_{2}+x_{3}=0$ statt durch $x_{3}=0$ .

Insbesondere in der Dreiecksgeometrie spielen die baryzentrischen Koordinaten, neben den trilinearen Koordinaten, eine wesentliche Rolle. Überall, wo es um Verhältnisse von Strecken geht, wie zum Beispiel in dem Satz von Ceva, sind sie ein geeignetes Werkzeug. Aber nicht nur in der Geometrie, sondern auch im Bereich des computer-aided Design verwendet man sie zur Erzeugung von dreieckigen Flächenstücken, den dreieckigen Bézierflächen.

In den Abschnitten Definition und Im Raum werden die in der Mathematik üblichen Bezeichnungen benutzt. In den Abschnitten Auf einer Gerade, In einer Ebene werden die Koordinaten mit $(m_{1}:m_{2}),(m_{1}:m_{2}:m_{3})$ bezeichnet, um an ihre Beziehung zu Massen und deren Schwerpunkt zu erinnern, was für das Verständnis oft eine Hilfe ist.

Definition und Eigenschaften

Definition

Es seien $\mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}$ die Ortsvektoren der Ecken $X_1, \dotsc, X_n$ eines Simplex in einem affinen Raum $\mathcal A$ . Der affine Raum hat dann die Dimension n-1 . Falls es für einen Punkt $P:\mathbf {p}$ in $\mathcal A$ Zahlen $\;a_{1},\dotsc ,a_{n}$ gibt, deren Summe nicht Null ist und die Gleichung

(G) $\quad (a_{1}+\dotsb +a_{n})\mathbf {p} =a_{1}\,\mathbf {x} _{1}+\dotsb +a_{n}\,\mathbf {x} _{n}\ ,$

erfüllt, sagt man $a_1, \dotsc, a_n$ sind baryzentrische Koordinaten des Punktes bezüglich der Punkte $X_{1},\dotsc X_{n}$ und schreibt $P=(a_{1}:\dotsc :a_{n})$ . Für die Ecken gilt offensichtlich

$\;X_{1}=(1:0:0:\ldots :0),\;X_{2}=(0:1:0\dotsc :0)\dotsc ,\;X_{n}=(0:0:0:\dotsc :1)\;$ .

Baryzentrische Koordinaten sind nicht eindeutig: Für jedes $\lambda$ ungleich Null beschreibt auch $(\lambda a_{1}:\dotsc :\lambda a_{n})$ den Punkt . D.h.: Nur die Verhältnisse der Koordinaten sind wesentlich. An diese Eigenschaft soll die Schreibweise mit erinnern. Man kann baryzentrische Koordinaten als homogene Koordinaten eines (n-1) -dimensionalen projektiven Raums $\mathcal P$ auffassen, von dem der affine Raum $\mathcal A$ ein Teil ist. Und zwar sind die Punkte von $\mathcal A$ diejenigen Punkte von $\mathcal P$ , die nicht in der durch die Gleichung $\;a_{1}+\dotsb +a_{n}=0\;$ bestimmten Hyperebene (Fernhyperebene) liegen.

Gleichung (G) ist ein unterbestimmtes homogenes lineares Gleichungssystem, das sich in der üblichen Form

(G') $\quad a_{1}(\mathbf {p} -\mathbf {x} _{1})+\dotsb +a_{n}(\mathbf {p} -\mathbf {x} _{n})=\mathbf {0}$

schreiben lässt.

Erfüllen die Koordinaten $a_{1},\dotsc a_{n}$ zusätzlich die Normierungsbedingung

(N) $\quad a_{1}+\dotsb +a_{n}=1\ ,$

so spricht man von normierten baryzentrischen Koordinaten. In diesem Fall sind die Zahlen $a_{1},...a_{n}$ eindeutig bestimmt (s. unten) und man kann den Punkt (Ursprungsgerade) auch als affinen Punkt $(a_{1},...,a_{n})$ der Hyperebene des $\mathbb {R} ^{n}$ mit der Gleichung $a_{1}+...+a_{n}=1$ auffassen. Um die Normierung formal sicher zu stellen, kann man (N) nach einer Koordinate auflösen und in das n-tupel einfügen. Löst man z.B. nach $a_{n}$ auf, ergibt sich $P=(a_{1}:...:1-a_{1}-...-a_{n-1})$ .

Hinweis: Die Begriffe werden nicht einheitlich verwendet. Viele Autoren sprechen nur dann von baryzentrischen Koordinaten, wenn die Normierungsbedingung erfüllt ist.
Normierte baryzentrische Koordinaten lassen sich einfach ermitteln, indem man jede einzelne baryzentrische Koordinate durch die Summe der Koordinaten dividiert.

Eigenschaften

Punkt im Simplex:
Falls die Koordinaten positiv sind, so liegt der Punkt in der konvexen Hülle von $X_{1},\dotsc ,X_{n}$ , also im Simplex mit diesen Eckpunkten. Die Darstellung eines Punktes innerhalb einer konvexen Hülle als Summe von Eckpunkten eines Simplex wird affine Kombination oder baryzentrische Kombination genannt.

Massenmittelpunkt:
Wie man aus der Umstellung

(S) $\quad \mathbf {p} ={\frac {a_{1}\mathbf {x} _{1}+\dotsb +a_{n}\mathbf {x} _{n}}{a_{1}+\dotsb +a_{n}}}$

der Definitionsgleichung (G) sieht, kann man als Massenmittelpunkt (das Baryzentrum) einer Anordnung von Massen $a_1, \dotsc, a_n$ an den Eckpunkten $X_1, \dotsc, X_n$ des Simplex auffassen. Dies ist der Ursprung des Begriffs baryzentrisch.
Physikalische Bedeutung der
Gleichung (G): Die Gesamtmasse im Schwerpunkt verursacht im Nullpunkt dasselbe Drehmoment wie die Einzelmassen,
Gleichung (G'): Die Summe der von den Einzelmassen erzeugten Drehmomente ist im Schwerpunkt gleich 0.

Mittelpunkt zweier Punkte:
Sind $(p_{1}:...:p_{n}),(q_{1}:...:q_{n})$ die normierten (!) baryzentrischen Darstellungen zweier Punkte $P:\mathbf {p} ,Q:\mathbf {q}$ , dann hat der Mittelpunkt $M:{\tfrac {1}{2}}(\mathbf {p} +\mathbf {q} )$ die baryzentrische Darstellung

$M=({\frac {p_{1}+q_{1}}{2}}:...:{\frac {p_{n}+q_{n}}{2}})=(p_{1}+q_{1}:...:p_{n}+q_{n})\ .$

Existenz, Eindeutigkeit normierter Koordinaten:
Normierte baryzentrische Koordinaten sind eindeutig bestimmt. Denn, versucht man das durch (G') und (N) beschriebene inhomogene lineare Gleichungssystem mit Hilfe der Cramerschen Regel zu lösen, ist die Determinante im Nenner ungleich Null, da sie, bis auf einen Faktor, im ebenen Fall (n=3) die orientierte Fläche des Dreiecks und im 3-dimensionalen Fall (n=4) das orientierte Volumen des Tetraeders ist (siehe unten).

Lässt man die Bedingung (N) wieder fallen, hat das lineare homogene System (G') 1-dimensionale Lösungen (Punkte des oben erwähnten projektiven Raums $\mathcal P$ ). Für größeres gilt Entsprechendes.

Unabhängigkeit von Nullpunkt und Skalierung:
Dass die baryzentrischen Koordinaten nicht von dem zufällig gewählten Nullpunkt des affinen Raums $\mathcal A$ abhängen, erkennt man dadurch, dass eine Verschiebung der Vektoren $\mathbf {p} ,\mathbf {x} _{1},...$ um einen festen Vektor ${\mathbf {v}}$ die Definitionsgleichung (G) unverändert lässt. Dasselbe gilt für eine uniforme Skalierung (Multiplikation der Vektoren mit einem festen Faktor ungleich Null).

Beispiel:
In der Ebene besteht ein Simplex aus 3 Punkten (Dreieck), d.h. es ist n=3 und jeder Punkt hat 3 baryzentrische Koordinaten: $P=(a_{1}:a_{2}:a_{3})$ . Zum Beispiel hat der geometrische Schwerpunkt des Dreiecks die baryzentrische Darstellung $\;S=(1:1:1)\;$ , denn es ist $\;\mathbf {s} ={\tfrac {1}{3}}(\mathbf {x} _{1}+\mathbf {x} _{2}+\mathbf {x} _{3})\;.$ Die normierte Darstellung ist $\;S=({\tfrac {1}{3}}:{\tfrac {1}{3}}:{\tfrac {1}{3}})\;.$

Vorteil, Nachteil:
Wie man in dem Beispiel sieht, lassen sich wesentliche Punkte z.B. von Dreiecken einheitlich und einfach beschreiben. Bei Berechnungen müssen nicht die speziellen (affinen) Koordinaten eines gegebenen Dreiecks berücksichtigt werden. Wie man affine Koordinaten in baryzentrische Koordinaten umrechnet, wird in den folgenden Abschnitten gezeigt. Ein gewisser Nachteil baryzentrischer Koordinaten ist allerdings: Sie sind nicht eindeutig (im nicht normierten Fall) und es gibt immer 1 Koordinate mehr als die affinen Koordinaten.

Unterschied zu anderen homogenen Koordinaten: Beispiel n=3
Üblicherweise führt man homogene Koordinaten so ein, dass die Ferngerade durch eine Koordinatenebene, z.B. durch $a_{3}=0$ , beschrieben wird. Dies hat den Vorteil, dass ein einfacher Zusammenhang zu den affinen Koordinaten, die die zugehörige affine Ebene (projektive Ebene ohne die Punkte der Ferngerade) beschreiben, besteht: Ein affiner Punkt hat die Koordinaten $(a_{1},a_{2})=(a_{1}:a_{2}:1)$ . Es besteht allerdings der Nachteil, dass die zu den Koordinatenachsen gehörigen projektiven Punkte $(1:0:0),(0:1:0)$ keine affinen Punkte sind. Nur der Punkt $(0:0:1)$ wird zu einem affinen Punkt. Baryzentrische Koordinaten haben keine so einfache Beziehung zu den affinen Koordinaten. Dafür liegen alle den Koordinatenachsen entsprechenden projektiven Punkte $(1:0:0),(0:1:0),(0:0:1)$ im affinen Bereich, denn die Ferngerade wird hier durch die Gleichung $a_{1}+a_{2}+a_{3}=0$ beschrieben.

Auf einer Gerade (n=2, Strecke)

Der Schwerpunkt $X_{s}$ zweier Massen $m_{1},m_{2}$ , die auf der -Achse an den Stellen $x_{1},x_{2}$ platziert sind, ist die Stelle $x_{s}$ , wo das Hebelgesetz (Kraft x Kraftarm = Last x Lastarm, siehe 2. Bild) erfüllt ist. Genauer: Wo die Summe der Drehmomente gleich Null ist und damit gilt:

(G'2) $\ m_{1}(x_{s}-x_{1})+m_{2}(x_{s}-x_{2})=0$

Diese Gleichung ist äquivalent zu (siehe Abschnitt Definition)

(G2) $\ (m_{1}+m_{2})x_{s}=m_{1}x_{1}+m_{2}x_{2}\;.$

Auflösen nach $x_{s}$ ergibt:

(S2) $\ x_{s}={\frac {m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}}$

Lässt man negative Massen zu, z.B. $m_{1}=1,m_{2}=-1+{\tfrac {1}{n}}$ , so ergibt sich aus (G2) für $n\to \infty$ die Gesamtmasse $m_{1}+m_{2}=0$ und $x_{s}=\infty$ .

Eine Lösung von (G'2) ist $\;m_{1}=x_{2}-x_{s},\;m_{2}=x_{s}-x_{1}\;$ . Alle Lösungen sind Vielfache davon. Also hat der Schwerpunkt die baryzentrische Darstellung (siehe Abschnitt Definition)

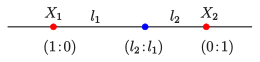
Baryzentrische Koordinaten als Verhältnis von Strecken

(B2) $\;X_{s}=(m_{1}:m_{2})=(x_{2}-x_{s}:x_{s}-x_{1})=(l_{\color {red}2}:l_{\color {red}1})$

Dabei ist $\;l_{1}=x_{s}-x_{1},\;l_{2}=x_{2}-x_{s}\;.$

Baryzentrische Koordinaten auf einer Gerade (unten). Der Mittelpunkt der Strecke $X_{1},X_{2}$ hat die baryzentrischen Koordinaten $(1:1)=({\tfrac {1}{2}}:{\tfrac {1}{2}})$

Dieser einfache Zusammenhang der baryzentrischen Koordinaten mit Verhältnissen von Teilstrecken ist der Grund für ihre Bedeutung in der Dreiecksgeometrie.
Die Aussage (B2) ist der Lehrsatz in §21, S. 25, des Buches von Möbius.

Die normierten baryzentrischen Koordinaten müssen zusätzlich zu (G'2) die Bedingung

(N2) $\quad m_{1}+m_{2}=1$

erfüllen. Löst man das inhomogene Gleichungssystem bestehend aus den Gleichungen (G'2), (N2) mit Hilfe der Cramerschen Regel, ergibt sich die normierte Darstellung

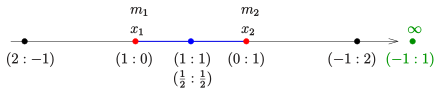
(NB2) $\ X_{s}={\big (}{\frac {x_{2}-x_{s}}{x_{2}-x_{1}}}\;:\;{\frac {x_{s}-x_{1}}{x_{2}-x_{1}}}{\big )}={\big (}{\frac {l_{2}}{l_{1}+l_{2}}}:{\frac {l_{1}}{l_{1}+l_{2}}}{\big )}\;.$

Beispiel: Der Mittelpunkt ${\tfrac {x_{1}+x_{2}}{2}}$ der Punkte $x_{1},x_{2}$ besitzt die baryzentrischen Koordinaten $(1:1)$ und in normierter Darstellung $({\tfrac {1}{2}}:{\tfrac {1}{2}})\;.$

In einer Ebene (n=3, Dreieck)

Umrechnung der Koordinaten

Sind in den Ecken eines Dreiecks $\;X_{1}=(x_{1},y_{1}),\;X_{2}=(x_{2},y_{2}),\;X_{3}=(x_{3},y_{3}),\;$ drei Massen $m_{1},m_{2},m_{3}$ platziert, so sind die Gleichgewichtsgleichungen für die Drehmomente um die Koordinatenachsen

(G'3) $\quad {\begin{array}{r}m_{1}(x_{s}-x_{1})+m_{2}(x_{s}-x_{2})+m_{3}(x_{s}-x_{3})=0\\m_{1}(y_{s}-y_{1})+m_{2}(y_{s}-y_{2})+m_{3}(y_{s}-y_{3})=0\end{array}}$

oder in der Form (siehe Definition)

(G3) $\quad {\begin{array}{c}(m_{1}+m_{2}+m_{3})x_{s}=m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}\\(m_{1}+m_{2}+m_{3})y_{s}=m_{1}y_{1}+m_{2}y_{2}+m_{3}y_{3}\end{array}}$

Der Schwerpunkt hat die Koordinaten

(S3) $\quad {\begin{array}{c}x_{s}=\displaystyle {\frac {m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}}{m_{1}+m_{2}+m_{3}}}\\y_{s}=\displaystyle {\frac {m_{1}y_{1}+m_{2}y_{2}+m_{3}y_{3}}{m_{1}+m_{2}+m_{3}}}.\end{array}}$

Baryzentrische Koordinaten eines gegebenen Punktes $S=({\color {red}x_{s}},{\color {red}y_{s}})$ , erhält man durch Lösen des unterbestimmten homogenen Systems (G'3) nach $m_{1},m_{2},m_{3}$ . Nimmt man die Normierungsgleichung

(N3) $\quad m_{1}+m_{2}+m_{3}=1$

hinzu, ist das jetzt inhomogene LGS eindeutig und mit Hilfe der Cramerschen Regel lösbar. Es ergibt sich:

$S=(x_{s},y_{s}),\;X_{i}=(x_{i},y_{i})$

(NB3) $\qquad {\begin{array}{l}m_{1}=\displaystyle {\frac {(x_{2}-{\color {red}x_{s}})(y_{3}-{\color {red}y_{s}})-(x_{3}-{\color {red}x_{s}})(y_{2}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\m_{2}=\displaystyle {\frac {(x_{3}-{\color {red}x_{s}})(y_{1}-{\color {red}y_{s}})-(x_{1}-{\color {red}x_{s}})(y_{3}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\m_{3}=\displaystyle {\frac {(x_{1}-{\color {red}x_{s}})(y_{2}-{\color {red}y_{s}})-(x_{2}-{\color {red}x_{s}})(y_{1}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\\end{array}}$

Der gemeinsame Nenner ist der doppelte Flächeninhalt des Dreiecks, also ungleich Null.

Wegen $m_{1}+m_{2}+m_{3}=1$ genügt es, zwei der drei Brüche zu berechnen.

Alle Zähler lassen sich als $2\times 2$ -Determinanten schreiben. Verzichtet man auf die Normierung, darf bei den baryzentrischen Koordinaten der gemeinsame Nenner weggelassen werden:

(B3) $\quad (m_{1}:m_{2}:m_{3})={\Big (}\left|{\begin{array}{l}x_{2}\!-\!{\color {red}x_{s}}&x_{3}\!-\!{\color {red}x_{s}}\\y_{2}\!-\!{\color {red}y_{s}}&y_{3}\!-\!{\color {red}y_{s}}\\\end{array}}\right|:\left|{\begin{array}{l}x_{3}\!-\!{\color {red}x_{s}}&x_{1}\!-\!{\color {red}x_{s}}\\y_{3}\!-\!{\color {red}y_{s}}&y_{1}\!-\!{\color {red}y_{s}}\\\end{array}}\right|:\left|{\begin{array}{l}x_{1}\!-\!{\color {red}x_{s}}&x_{2}\!-\!{\color {red}x_{s}}\\y_{1}\!-\!{\color {red}y_{s}}&y_{2}\!-\!{\color {red}y_{s}}\\\end{array}}\right|{\Big )}$

Multipliziert man jede Determinante mit ${\tfrac 12}$ , entstehen die orientierten Flächen $\Delta _{1},\Delta _{2},\Delta _{3}$ der Teildreiecke $X_{2}X_{3}S$ , $X_{1}X_{3}S$ , $X_{1}X_{2}S$ (siehe auch den nächsten Abschnitt Beziehung zu trilineare Koordinaten). Damit gilt:

(BF3) $\qquad (m_{1}:m_{2}:m_{3})=(\Delta _{1}:\Delta _{2}:\Delta _{3})$

Aussage (BF3) ist der Lehrsatz in §23, S. 26, des Buches von Möbius.

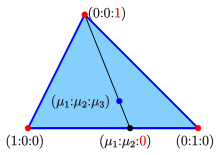
Spezialfall: Koordinatendreieck:

Für das spezielle rechtwinklige Dreieck $\;X_{3}=(0,0),X_{1}=(1,0),X_{2}=(0,1)\;$ als Bezugsdreieck hat ein Punkt (x,y) die einfachen baryzentrischen Koordinaten $(x:y:1-x-y)$ .

Geraden, Schnittpunkte, Parallelität

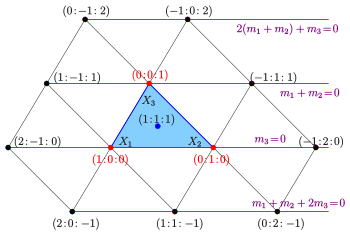
In den Punkten $X_{1},X_{2},X_{3}$ befinden sich die Massen $m_{1},m_{2},m_{3}$ .
Die lilafarbigen parallelen Geraden haben die jeweils angegebenen Gleichungen. Ihr gemeinsamer Fernpunkt hat die Koordinaten $(-1:1:0).$
Die Koordinaten der Rasterpunkte sind normiert.

Die Ecken des Dreiecks haben die homogenen Koordinaten

$X_{1}=(1\!:\!0\!:\!0),\;X_{2}=(0\!:\!1\!:\!0),\;X_{3}=(0\!:\!0\!:\!1)\;$ .

Die Gerade durch die Punkte $X_{1},X_{2}$ wird durch die Gleichung $m_{3}=0$ beschrieben und hat den Fernpunkt $(-1:1:0)$ . …
Die Ferngerade ist durch die Gleichung $\;m_{1}+m_{2}+m_{3}=0\;$ festgelegt.
Eine beliebige Gerade wird durch eine Gleichung $\;am_{1}+bm_{2}+cm_{3}=0\;$ beschrieben (s. homogene Koordinaten).
Drei Geraden

$a_{1}m_{1}+b_{1}m_{2}+c_{1}m_{3}=0,$

$a_{2}m_{1}+b_{2}m_{2}+c_{2}m_{3}=0,$

$a_{3}m_{1}+b_{3}m_{2}+c_{3}m_{3}=0$

haben einen Punkt gemeinsam, wenn

$\qquad \quad \left|{\begin{matrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{matrix}}\right|=0$ .

Zwei Geraden $\;a_{1}m_{1}+b_{1}m_{2}+c_{1}m_{3}=0,\;a_{2}m_{1}+b_{2}m_{2}+c_{2}m_{3}=0\;$ sind parallel, wenn sie sich auf der Ferngerade schneiden, d.h., wenn

$\qquad \quad \left|{\begin{matrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\1&1&1\end{matrix}}\right|=0$ .

Drei Punkte $(m_{1}:m_{2}:m_{3})$ , $(m'_{1}:m'_{2}:m'_{3})$ und $(m''_{1}:m''_{2}:m''_{3})$ liegen genau dann auf einer Geraden, wenn

$\qquad \quad \left|{\begin{matrix}m_{1}&m_{2}&m_{3}\\m'_{1}&m'_{2}&m'_{3}\\m''_{1}&m''_{2}&m''_{3}\end{matrix}}\right|=0.$

Hieraus ergibt sich die Gleichung $\;am_{1}+bm_{2}+cm_{3}=0\;$ einer Gerade durch zwei vorgegebene Punkte $(u_{1}:u_{2}:u_{3}),(v_{1}:v_{2}:v_{3})$ in Determinantenform:

$\qquad \quad \left|{\begin{matrix}m_{1}&m_{2}&m_{3}\\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\end{matrix}}\right|=0$

Beziehung zu trilinearen Koordinaten

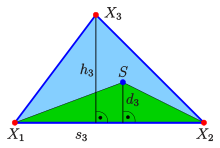
Grundseite und Höhe eines Teildreiecks

Für die Flächen $\Delta _{1},\Delta _{2},\Delta _{3}$ der Teildreiecke in (BF3) gilt $\Delta _{i}={\frac {1}{2}}s_{i}d_{i}$ , wobei $s_{i},d_{i}$ die Grundseiten (Seiten des Dreiecks) und die Höhen der Teildreiecke sind (siehe Bild). Also gilt

(BT3) $\ (m_{1}:m_{2}:m_{3})=(s_{1}d_{1}:s_{2}d_{2}:s_{3}d_{3})\ ,$

Die Beziehung (BT3) zeigt den einfachen Zusammenhang der baryzentrischen Koordinaten mit den trilinearen Koordinaten $(d_{1}:d_{2}:d_{3})$ eines Punktes. Für ein gleichseitiges Dreieck sind die baryzentrischen und trilinearen Koordinaten gleich. Die Ferngerade hat in baryzentrischen Koordinaten die Gleichung $\;m_{1}+m_{2}+m_{3}=0\;$ . In trilinearen Koordinaten ist die Gleichung noch von den Seitenlängen $s_{i}$ des Dreiecks abhängig: $\;s_{1}d_{1}+s_{2}d_{2}+s_{3}d_{3}=0\;.$

Besondere Punkte, Eulergerade

geometrischer Schwerpunkt

ist der geometrische Schwerpunkt, wenn alle Massen gleich sind. Seine baryzentrischen Koordinaten sind also $\;(1:1:1)\;.$ Wegen (BF3) und $\Delta ={\tfrac {1}{2}}s_{i}h_{i}\;,\;\Delta _{i}={\tfrac {1}{2}}s_{i}d_{i}$ gilt

$\quad \Delta _{i}={\frac {1}{3}}\Delta \quad$ und $\quad d_{i}={\frac {1}{3}}h_{i}\;.$

(Siehe hierzu auch Geometrischer Schwerpunkt.)

Parameterdarstellung einer Gerade

Eine Gerade durch zwei Punkte $A=(a_{1}:a_{2}:a_{3}),B=(b_{1}:b_{2}:b_{3})$ hat für Punkte $\neq B$ die Darstellung

$X(t)={\big (}a_{1}+tb_{1}:a_{2}+tb_{2}:a_{3}+tb_{3}{\big )}\ ,\ t\in \mathbb {R} \;.$

Projektion eines Punktes auf die Seite gegenüber einer Ecke

Projektion auf eine Seite

Projiziert man einen Punkt $P=(\mu _{1}:\mu _{2}:\mu _{3})$ von der Ecke $X_{3}=(0:0:1)$ aus auf die gegenüberliegende Seite (die Gerade hat die Gleichung $m_{3}=0$ ), so erhält man den Punkt $Y_{3}=(\mu _{1}:\mu _{2}:0)$ (siehe Bild). Sind die Koordinaten von normiert, teilt die Strecke $X_{3}Y_{3}$ im Verhältnis $(1-\mu _{3}):\mu _{3}$ . Ist z.B. der Punkt der geometrische Schwerpunkt , so wird er auf die Seitenmitte $S_{3}$ projiziert und teilt die Strecke $X_{3}S_{3}$ im Verhältnis 2:1 .
Entsprechendes gilt für die Projektionen von den anderen Ecken aus.

Inkreismittelpunkt, Ankreismittelpunkte

Zu Inkreismittelpunkt und Ankreismittelpunkte:
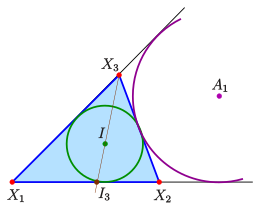
Die Flächeninhalte der Dreiecke $X_{1}X_{2}X_{3}$ und $A_{1}X_{2}X_{3}$ haben verschiedene Vorzeichen

Für den Inkreis des Dreiecks gilt $d_{i}=r$ (Inkreisradius) und damit (s. (BT3)) hat der Inkreismittelpunkt die baryzentrischen Koordinaten $(s_{1}:s_{2}:s_{3})$ und wegen $\;\Delta =\Delta _{1}+\Delta _{2}+\Delta _{3}={\tfrac {1}{2}}(s_{1}+s_{2}+s_{3})r\;$ gilt $\;r={\tfrac {2\Delta }{s_{1}+s_{2}+s_{3}}}\;.$ Mit Hilfe des Sinussatzes ergibt sich für den Inkreismittelpunkt auch eine Darstellung mit den Winkeln:

$I=(s_{1}:s_{2}:s_{3})=(\sin \varphi _{1}:\sin \varphi _{2}:\sin \varphi _{3})\;,$

wobei $\varphi _{i}$ der Winkel bei $X_{i}$ ist.

Die Winkelhalbierende der Ecke $X_{3}$ (Gerade $X_{3}I$ ) hat die Gleichung

$s_{2}m_{1}-s_{1}m_{2}=0\ .$

Sie schneidet die Seite $X_{1}X_{2}$ (Gleichung $m_{3}=0$ ) im Punkt $I_{3}=(s_{1}:s_{2}:0)$ . ( $I_{3}$ kann auch als Projektion von auf die Seite $X_{1}X_{2}$ angesehen werden.) Wegen (B2) gilt:

$|X_{1}I_{3}|:|X_{2}I_{3}|=s_{2}:s_{1}\ .$ Analog für die anderen Winkelhalbierenden.

Dies ist der Winkelhalbierendensatz für das Dreieck $X_{1}X_{2}X_{3}$ .

Da die Dreiecksflächen orientiert sind, kann $\Delta_i$ und damit auch $d_{i}$ negative Werte annehmen, jenachdem, ob auf derselben Seite der zu $s_{i}$ gehörigen Dreiecksseite liegt wie die Ecke $X_{i}$ oder nicht. Beim Inkreismittelpunkt haben alle $d_{i}$ dasselbe Vorzeichen. Bei einem Ankreismittelpunkt haben (wie beim Inkreismittelpunkt) alle Abstände die Länge des Ankreisradius, aber einer der Abstände hat ein von den beiden anderen verschiedenes Vorzeichen. Damit ergeben sich die baryzentrischen Darstellungen der Ankreismittelpunkte:

$A_{1}=(-s_{1}:s_{2}:s_{3}),\quad A_{2}=(s_{1}:-s_{2}:s_{3}),\quad A_{3}=(s_{1}:s_{2}:-s_{3})\ .$

Analog zum Inkreisradius ergibt sich für die Ankreisradien:

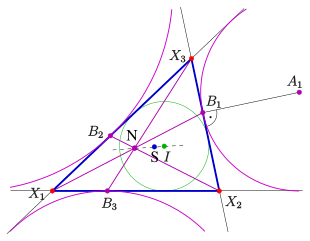
$r_{1}={\frac {2\Delta }{-s_{1}+s_{2}+s_{3}}},\quad r_{2}={\frac {2\Delta }{s_{1}-s_{2}+s_{3}}},\quad r_{3}={\frac {2\Delta }{s_{1}+s_{2}-s_{3}}}\ .$

: Nagel-Punkt. Er liegt mit dem geometrischen Schwerpunkt und dem Inkreismittelpunkt auf einer Gerade. teilt die Strecke $NI$ im Verhältnis 2:1

Nagelpunkt

Aus der Beschreibung der Lage der Berührpunkte der Ankreise auf den Dreiecksseiten erkennt man ihre baryzentrische Darstellung:

$B_{1}=(0:s_{1}-s_{2}+s_{3}:s_{1}+s_{2}-s_{3}),$

$B_{2}=(-s_{1}+s_{2}+s_{3}:0:s_{1}+s_{2}-s_{3}),$

$B_{3}=(-s_{1}+s_{2}+s_{3}:s_{1}-s_{2}+s_{3}:0)\ .$

B_i ist offensichtlich die Projektion (siehe oben) des Punktes

$N=(-s_{1}+s_{2}+s_{3}:s_{1}-s_{2}+s_{3}:s_{1}+s_{2}-s_{3})$

von der Ecke $X_{i}$ aus auf die gegenüberliegende Seite. D.h.:

Die drei Geraden ${\overline {X_{1}B_{1}}},{\overline {X_{2}B_{2}}},{\overline {X_{3}B_{3}}}$ schneiden sich im Punkt , dem Nagel-Punkt.

Die Matrix

${\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\end{pmatrix}}$

beschreibt (in baryzentrischen Koordinaten) die zentrische Streckung am geometrischen Schwerpunkt mit dem Faktor $-\tfrac12$ (siehe Abschnitt Steiner-Ellipse, Steiner-Inellipse). Bildet man damit ab, erhält man den Inkreismittelpunkt . Dies zeigt:

Die Punkte $N,S,I$ liegen auf einer Gerade durch und teilt die Strecke $NI$ im Verhältnis 2:1.

Umkreismittelpunkt

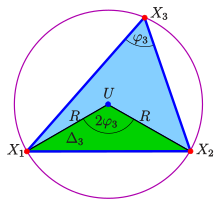
Umkreismittelpunkt

Der Umkreismittelpunkt hat zu den Ecken den gleichen Abstand , den Umkreisradius. Der Winkel bei im Teildreieck $X_{1},X_{2},U$ ist wegen des Kreiswinkelsatzes doppelt so groß wie der Winkel $\varphi_3$ bei $X_{3}$ . Also ist die Fläche $\Delta _{3}={\tfrac {1}{2}}R^{2}\sin 2\varphi _{3}$ . Entsprechendes gilt für $\Delta _{1},\Delta _{2}$ . Damit sind die baryzentrischen Koordinaten des Umkreismittelpunktes

$(\sin 2\varphi _{1}:\sin 2\varphi _{2}:\sin 2\varphi _{3})\ .$

Aus $\;\sin 2\varphi _{i}=2\sin \varphi _{i}\cos \varphi _{i},\;\sin \varphi _{i}={\tfrac {s_{i}}{2R}}\;$ und den Kosinussätzen für die drei Winkel ergibt sich die winkelfreie Darstellung

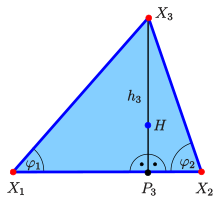
${\big (}s_{1}^{2}(-s_{1}^{2}+s_{2}^{2}+s_{3}^{2}):s_{2}^{2}(s_{1}^{2}-s_{2}^{2}+s_{3}^{2}):s_{3}^{2}(s_{1}^{2}+s_{2}^{2}-s_{3}^{2}){\big )}\ .$

Höhenschnittpunkt

Höhenschnittpunkt

Ist $H=(m_{1}:m_{2}:m_{3})$ der Höhenschnittpunkt, so ist $P_{3}=(m_{1}:m_{2}:0)$ der Fußpunkt der Höhe $h_{3}$ (siehe Bild) und es gilt $\;\tan \varphi _{1}={\tfrac {h_{3}}{|P_{3}X_{1}|}},\;\tan \varphi _{2}={\tfrac {h_{3}}{|P_{3}X_{2}|}}\;$ Wegen (B2) ist $\;\tan \varphi _{1}:\tan \varphi _{2}=|P_{3}X_{2}|:|P_{3}X_{1}|=m_{1}:m_{2}\;.$ Analog ergeben sich die anderen Verhältnisse. Damit hat der Höhenschnittpunkt die baryzentrischen Koordinaten

$(\tan \varphi _{1}:\tan \varphi _{2}:\tan \varphi _{3})\ .$

Falls ein Winkel $90^{\circ }$ ist, z.B. $\varphi _{3}=90^{\circ }$ , so ist $H=X_{3}$ .

Spieker-Punkt

Spieker-Punkt eines Dreiecks

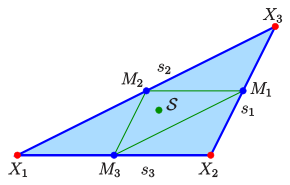
Belegt man die Seiten $X_{2}X_{3},X_{3}X_{1},X_{1}X_{2}$ eines Dreiecks $X_{1}X_{2}X_{3}$ gleichmäßig mit Masse, so nennt man den zugehörigen Kantenschwerpunkt Spieker-Punkt. (Ecken- und Flächenschwerpunkt eines Dreiecks sind identisch: der Schnittpunkt der Seitenhalbierenden.) Denkt man sich die Masse einer Seite in ihrem Schwerpunkt, dem Mittelpunkt $M_{i}$ konzentriert, so ist der Spieker-Punkt ${\mathcal {S}}=(x_{s},y_{s})$ der Schwerpunkt des Dreiecks $M_{1}M_{2}M_{3}$ mit den Seitenlängen $s_{1},s_{2},s_{3}$ als Massenbelegungen in den Ecken. Aus $M_{1}=({\tfrac {x_{2}+x_{3}}{2}},{\tfrac {y_{2}+y_{3}}{2}}),...$ und (S3) folgt:

$x_{s}={\frac {s_{1}{\frac {x_{2}+x_{3}}{2}}+s_{2}{\frac {x_{1}+x_{3}}{2}}+s_{3}{\frac {x_{1}+x_{2}}{2}}}{s_{1}+s_{2}+s_{3}}}$

$\quad ={\frac {(s_{2}+s_{3})x_{1}+(s_{1}+s_{3})x_{2}+(s_{1}+s_{2})x_{3}}{2(s_{1}+s_{2}+s_{3})}}\ .$

Analog ergibt sich die y-Koordinate.

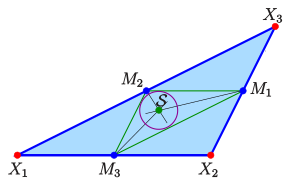
Spieker-Punkt als Mittelpunkt des Inkreises des Dreiecks $M_{1}M_{2}M_{3}$

Hieraus erkennt man die baryzentrischen Koordinaten des Spieker-Punktes:

${\mathcal {S}}=(s_{2}+s_{3}:s_{1}+s_{3}:s_{1}+s_{2})\ .$

Bedeutung von ${\mathcal {S}}$ für das Dreieck $M_{1}M_{2}M_{3}$ :
Aus den obigen Überlegungen (Masse $s_{i}$ im Punkt $M_{i}$ ) folgt direkt die baryzentrische Darstellung von ${\mathcal {S}}$ bezüglich des (grünen) Dreiecks $M_{1}M_{2}M_{3}$ :

${\mathcal {S}}=(s_{1}:s_{2}:s_{3})_{M}={\big (}{\tfrac {s_{1}}{2}}:{\tfrac {s_{2}}{2}}:{\tfrac {s_{3}}{2}}{\big )}_{M}$

Da ${\tfrac {s_{i}}{2}}$ die Länge der dem Punkt $M_{i}$ gegenüberliegenden (grünen) Seite ist, ist ${\mathcal {S}}$ der Inkreismittelpunkt = Schnittpunkt der Winkelhalbierenden des Dreiecks $M_{1}M_{2}M_{3}$ (siehe oben). Diese Eigenschaft liefert die Möglichkeit den Punkt ${\mathcal {S}}$ zeichnerisch zu bestimmen.

Eulergerade

Eulergerade eines Dreiecks

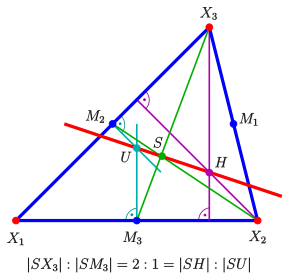
Der geometrische Schwerpunkt , der Umkreismittelpunkt und der Höhenschnittpunkt liegen auf einer Gerade, der Eulergerade. Denn, führt man am Punkt eine zentrische Streckung mit Streckfaktor $-{\tfrac 12}$ durch, wird jede Ecke auf den Mittelpunkt der ihr gegenüberliegenden Seite abgebildet ( teilt jede Seitenhalbierende im Verhältnis 2:1) und die Höhen werden auf die Mittelsenkrechten abgebildet. Also geht in über und beide Punkte liegen auf einer gemeinsamen Gerade durch . Der Umkreis geht dabei in den Kreis durch die Seitenmitten, den Feuerbachkreis, über, dessen Mittelpunkt (Bild von ) also auch auf der Eulergerade liegt.

Die Gleichung der Eulergerade in baryzentrischen Koordinaten ist (s. oben)

$\ \left|{\begin{matrix}m_{1}&m_{2}&m_{3}\\1&1&1\\\sin 2\varphi _{1}&\sin 2\varphi _{2}&\sin 2\varphi _{3}\end{matrix}}\right|=$

$\ m_{1}(\sin 2\varphi _{3}-\sin 2\varphi _{2})+m_{2}(\sin 2\varphi _{1}-\sin 2\varphi _{3})+m_{3}(\sin 2\varphi _{2}-\sin 2\varphi _{1})=0\$

oder unter Verwendung von Punkt :

$\ m_{1}(\tan \varphi _{3}-\tan \varphi _{2})+m_{2}(\tan \varphi _{1}-\tan \varphi _{3})+m_{3}(\tan \varphi _{2}-\tan \varphi _{1})=0\ .$

Gleichseitige Dreiecke besitzen keine Eulergerade, da $S=H=U$ ist.

Ist das Dreieck gleichschenklig, aber nicht gleichseitig, z.B. $\varphi _{1}=\varphi _{2}$ , so hat die Eulergerade die Gleichung $\;m_{1}-m_{2}=0\;$ und ist gleich der Seitenhalbierenden durch $X_{3}$ . Sie enthält dann auch den Inkreismittelpunkt.

Ist das Dreieck rechtwinklig, z.B. $\varphi _{3}=90^{\circ }$ , so ist $\varphi _{2}=90^{\circ }-\varphi _{1}\;\to \;\sin 2\varphi _{2}=\sin 2\varphi _{1}$ und die Eulergerade hat die Gleichung $\;m_{1}-m_{2}=0\;$ und ist die Seitenhalbierende zur Hypotenuse.

Satz von Ceva

Satz von Ceva

Satz von Ceva

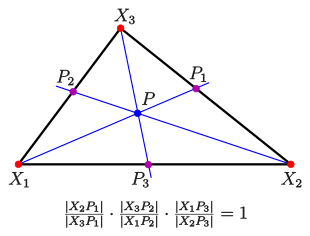
Ist P ein Punkt innerhalb des Dreiecks $X_{1},X_{2},X_{3}$ und $P_{i}$ der Schnittpunkt der Gerade ${\overline {PX_{i}}}$ mit der Seite $X_{j}X_{k}$ (siehe Bild), so gilt

${\frac {|X_{2}P_{1}|}{|X_{3}P_{1}|}}\cdot {\frac {|X_{3}P_{2}|}{|X_{1}P_{2}|}}\cdot {\frac {|X_{1}P_{3}|}{|X_{2}P_{3}|}}=1\;.$

Beweis

Mit den Punkten in baryzentrischen Koordinaten:

$X_{1}=(1:0:0),\;X_{2}=(0:1:0),\;X_{3}=(0:0:1)$

$P=(m_{1}:m_{2}:m_{3})$

ist $P_{1}=(0:m_{2}:m_{3})$ (siehe Besondere Punkte). Aus B2 erhält man $|X_{2}P_{1}|:|X_{3}P_{1}|=m_{3}:m_{2}\;.$ Führt man diese Überlegungen auch für diePunkte P_2,P_3 durch, ergibt sich

${\frac {|X_{2}P_{1}|}{|X_{3}P_{1}|}}\cdot {\frac {|X_{3}P_{2}|}{|X_{1}P_{2}|}}\cdot {\frac {|X_{1}P_{3}|}{|X_{2}P_{3}|}}={\frac {m_{3}}{m_{2}}}\cdot {\frac {m_{1}}{m_{3}}}\cdot {\frac {m_{2}}{m_{1}}}=1\;.$

Steiner-Ellipse, Steiner-Inellipse

Die eindeutig bestimmte Ellipse durch die Ecken des (beliebigen) Dreiecks $X_{1},X_{2},X_{3}$ , deren Mittelpunkt der geometrische Schwerpunkt ist, heißt Steiner-Ellipse. In baryzentrischen Koordinaten wird sie durch die Gleichung

(SE) $\quad m_{1}m_{2}+m_{2}m_{3}+m_{3}m_{1}=0$

beschrieben.

Steiner-Ellipse

Man prüft leicht nach, dass die sechs Punkte

$X_{1}=(1:0:0),\ X_{2}=(0:1:0),\ \ X_{3}=(0:0:1),$

$Y_{1}=(-1:2:2),Y_{2}=(2:-1:2),Y_{3}=(2:2:-1)\;$

die Gleichung (SE) erfüllen und, dass der Schwerpunkt $S=(1:1:1)$ der Mittelpunkt (siehe Abschnitt Definition) der Paare $X_{i},Y_{i}$ ist. Die Gleichung (SE) muss also einen nicht ausgearteten Kegelschnitt ${\mathcal {k}}$ (Ellipse oder Hyperbel oder Parabel) beschreiben. Da aus den Gleichungen

$m_{1}m_{2}+m_{2}m_{3}+m_{3}m_{1}=0,\quad m_{1}+m_{2}+m_{3}=0\quad$ der Widerspruch

$0=(m_{1}+m_{2}+m_{3})^{2}$

$\ =m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+2(m_{1}m_{2}+m_{2}m_{3}+m_{3}m_{1})$

$\ =m_{1}^{2}+m_{2}^{2}+m_{3}^{2}\neq 0\ .$

folgt, hat ${\mathcal {k}}$ mit der Ferngerade keinen Punkt gemeinsam, d.h. ${\mathcal {k}}$ ist eine Ellipse.

Die Spiegelung am Punkt lässt das Sechseck $X_{1}X_{2}X_{3}Y_{1}Y_{2}Y_{3}$ und damit auch die Ellipse invariant (Eine Ellipse ist durch 5 ihrer Punkte eindeutig bestimmt). Also ist der Symmetriepunkt der Mittelpunkt der Ellipse.

Da der Mittelpunkt $M_{3}$ der Sehne $X_{1}X_{2}$ auf dem Durchmesser $X_{3}Y_{3}$ liegt, muss die Tangente in $X_{3}$ parallel zu $X_{1}X_{2}$ sein (siehe Ellipse). Sie hat die Gleichung $m_{1}+m_{2}=0$ . Schneidet man die Parallele zur Tangente durch den Mittelpunkt (sie hat die Gleichung $m_{1}+m_{2}-2m_{3}=0$ ) mit der Ellipse (SE) erhält man die zwei zu $X_{3}$ konjugierten Punkte (siehe Steiner-Ellipse)

$D_{3}=(1-{\sqrt {3}}:1+{\sqrt {3}}:1),\quad D'_{3}=(1+{\sqrt {3}}:1-{\sqrt {3}}:1)\ .$

Entsprechendes gilt für die Tangenten in den anderen Ecken.

Steiner-Inellipse (grün)

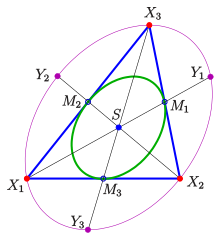
Bildet man die Steiner-Ellipse mit der zentrischen Streckung $\sigma$ an ihrem Mittelpunkt mit Faktor $-{\tfrac 12}$ ab, erhält man also eine Ellipse mit demselben Mittelpunkt , die die Dreiecksseiten in deren Mittelpunkten berührt. Dies ist die Steiner-Inellipse des Dreiecks. Wegen $\;M_{1}=(0:1:1),\;M_{2}=(1:0:1),\;M_{3}=(1:1:0)\;$ ist die Abbildungsmatrix von $\sigma$

${\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\end{pmatrix}}\ .$

Transformiert man die Gleichung (SE) der Steiner-Ellipse mit dieser Matrix, ergibt sich die Gleichung der Steiner-Inellipse in baryzentrischen Koordinaten:

(SIE) $\quad m_{1}^{2}+m_{2}^{2}+m_{3}^{2}-2(m_{1}m_{2}+m_{2}m_{3}+m_{3}m_{1})=0\ .$

Steiner-Ellipsen als Kegel in (homogenen) baryzentrischen Koordinaten und in normierten baryzentrischen Koordinaten als Kreise in der Ebene $m_{1}+m_{2}+m_{3}=1$

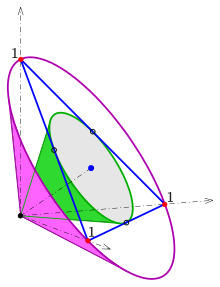
3d-Darstellungen

1) Die durch die Gleichung (SE) definierte Quadrik ${\mathcal {Q}}_{1}$ im $\mathbb {R} ^{3}$ mit (wie üblich) orthogonalen Koordinatenachsen ist ein gerader Kreiskegel mit dem Nullpunkt als Spitze, der die Koordinatenachsen enthält und die Gerade $t(1,1,1)^{T}$ als Achse besitzt. Denn für die Schnittkurve der Ebene $m_{1}+m_{2}+m_{3}=1$ und der Quadrik mit der Gleichung (SE) gilt

$1=(m_{1}+m_{2}+m_{3})^{2}$

$\ =m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+2(m_{1}m_{2}+m_{2}m_{3}+m_{3}m_{1})$

$\ =m_{1}^{2}+m_{2}^{2}+m_{3}^{2}\ .$

D.h.: die Schnittkurve ist auch ein ebener Schnitt der Einheitskugel und damit ein Kreis (im Bild lila).

2) Analoge Überlegungen für die durch die Gleichung (SIE) definierte Quadrik ${\mathcal {Q}}_{2}$ zeigen: ${\mathcal {Q}}_{2}$ ist auch ein gerader Kreiskegel mit dem Nullpunkt als Spitze und der Gerade $t(1,1,1)^{T}$ als Achse. Der Basiskreis ist der Schnitt der Ebene $m_{1}+m_{2}+m_{3}=1$ mit der kleineren Kugel $m_{1}^{2}+m_{2}^{2}+m_{3}^{2}={\tfrac {1}{2}}$ (im Bild grün). Schneidet man den Kegel ${\mathcal {Q}}_{2}$ mit der Koordinatenebene $m_{1}=0$ , ergibt sich die Ursprungsgerade $t(0,1,1)^{T}$ , d.h. der Kegel berührt die Koordinatenebene. Dies gilt auch für die anderen Koordinatenebenen.

3) In normierten baryzentrischen Koordinaten (d.h. in der Ebene $m_{1}+m_{2}+m_{3}=1$ ) erscheint das gegebene Dreieck gleichseitig und die Steiner-Ellipsen sind dessen Umkreis und Inkreis.

4) Setzt man keine orthogonalen Koordinaten des $\mathbb {R} ^{3}$ voraus, gilt nur: Die Kegel sind elliptisch, das Dreieck ist allgemein und die Kreise sind Ellipsen. Inzidenzen und Berührbeziehungen bleiben erhalten.

5) Wählt man, wie bei nicht baryzentrischen homogenen Koordinaten üblich, die Ursprungsebene $m_{3}=0$ als Ferngerade und setzt $x={\tfrac {m_{1}}{m_{3}}},y={\tfrac {m_{2}}{m_{3}}}$ , so beschreibt die Gleichung (SE) im affinen Bereich ( $m_{3}\neq 0$ ) die Hyperbel $y={\tfrac {1}{x+1}}-1$ . In diesem Fall sind die Punkte $(1:0:0),(0:1:0)$ Fernpunkte und zwar die Fernpunkte der Asymptoten. Im $\mathbb {R} ^{3}$ kann man sich die Hyperbel als Schnittkurve des Kegels ${\mathcal {Q}}_{1}$ mit der Ebene $m_{3}=1$ vorstellen.

6) Siehe hierzu auch: Inellipse.

Im Raum (n=4, Tetraeder)

Berechnung und Eigenschaften

Im 3-dimensionalen Raum ist ein Simplex ein Tetraeder mit den Ecken $\mathbf {x} _{1},\mathbf {x} _{2},\mathbf {x} _{3},\mathbf {x} _{4}$ . Um die baryzentrischen Koordinaten eines Punktes $\mathbf{p}$ bezgl. des gegebenen Tedraeders zu bestimmen, muss man, analog dem 2-dimensionalen Fall (Dreieck), das homogene lineare Gleichungssystem (siehe Abschnitt Definition)

(G'4) $\quad a_{1}(\mathbf {x} _{1}-\mathbf {p} )+a_{2}(\mathbf {x} _{2}-\mathbf {p} )+a_{3}(\mathbf {x} _{3}-\mathbf {p} )+a_{4}(\mathbf {x} _{4}-\mathbf {p} )=0$

für $a_{1},a_{2},a_{3},a_{4}$ lösen. Wie im ebenen Fall fügt man hier auch die Normierungsgleichung $a_{1}+a_{2}+a_{3}+a_{4}=1$ hinzu und löst das LGS mit Hilfe der Cramerschen Regel. Mit den Abkürzungen

$V_{1}={\frac {1}{6}}\det(\mathbf {x} _{2}-\mathbf {p} ,\mathbf {x} _{3}-\mathbf {p} ,\mathbf {x} _{4}-\mathbf {p} ),\quad V_{2}={\frac {1}{6}}\det(\mathbf {x} _{3}-\mathbf {p} ,\mathbf {x} _{4}-\mathbf {p} ,\mathbf {x} _{1}-\mathbf {p} ),$

$V_{3}={\frac {1}{6}}\det(\mathbf {x} _{4}-\mathbf {p} ,\mathbf {x} _{1}-\mathbf {p} ,\mathbf {x} _{2}-\mathbf {p} ),\quad V_{4}={\frac {1}{6}}\det(\mathbf {x} _{1}-\mathbf {p} ,\mathbf {x} _{2}-\mathbf {p} ,\mathbf {x} _{3}-\mathbf {p} )$

Baryzentrische Koordinaten bezgl. eines Tetraeders (im Raum)

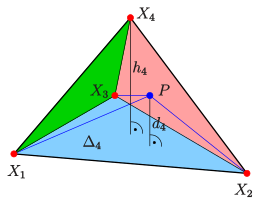
erhält man für die baryzentrischen Koordinaten von $\mathbf{p}$ :

(BV4) $\ (a_{1}:a_{2}:a_{3}:a_{4})=(V_{1}:V_{2}:V_{3}:V_{4})$

Dabei ist $V_{i}$ das Volumen des Teiltetraeders, der aus dem gegebenen Tetraeder entsteht, indem man ${\mathbf {x}}_{i}$ durch $\mathbf{p}$ ersetzt (s. Bild).

Aussage (BV4) ist der Lehrsatz in §25, S. 28, des Buches von Möbius.

Ist $\Delta_i$ die Grundfläche (Seitenfläche des Tedraeders) und $d_{i}$ die Höhe des -ten Teiltetraeders, so gilt $V_{i}={\tfrac {1}{3}}\Delta _{i}d_{i}$ und

$(a_{1}:a_{2}:a_{3}:a_{4})=(\Delta _{1}d_{1}:\Delta _{2}d_{2}:\Delta _{3}d_{3}:\Delta _{4}d_{4})\ .$

Besondere Punkte

Geometrischer Schwerpunkt

Der geometrische Schwerpunkt hat die baryzentrischen Koordinaten $(1:1:1:1)$ . Damit ist

$V_{i}={\frac {1}{3}}\Delta _{i}d_{i}={\frac {1}{4}}V={\frac {1}{4}}{\frac {1}{3}}\Delta _{i}h_{i}\;,$

wobei das Volumen des gegebenen Tetraeders und h_i die Höhe des -ten Punktes über dem -ten Seitendreieck (s. Bild) ist. Also gilt:

$d_{i}={\frac {h_{i}}{4}}$

(Vergleiche die entsprechende Aussage im ebenen Fall.)

Inkugelmittelpunkt

Für den Mittelpunkt der Inkugel ist $d_{i}=r$ (Radius der Inkugel) und damit

$(a_{1}:a_{2}:a_{3}:a_{4})=(\Delta _{1}:\Delta _{2}:\Delta _{3}:\Delta _{4})\$ und

$r={\frac {3V}{\Delta _{1}+\Delta _{2}+\Delta _{3}+\Delta _{4}}}\;,$

wobei $V=V_{1}+V_{2}+V_{3}+V_{4}$ das Volumen des gegebenen Tetraeders ist.

Projektion eines Punktes auf eine Koordinatenebene

Analog zum ebenen Fall (siehe oben) ist die Projektion eines Punktes $P=(\alpha _{1}:\alpha _{2}:\alpha _{3}:\alpha _{4})$ von $X_{1}=(1:0:0:0)$ aus auf die gegenüber liegende Ebene durch $X_{2},X_{3},X_{4}$ (sie hat die Gleichung $a_{1}=0$ ) der Punkt $\;Y_{1}=(0:\alpha _{2}:\alpha _{3}:\alpha _{4})\;$ . Falls die Koordinaten von normiert sind, teilt die Strecke $X_{1}Y_{1}$ im Verhältnis $(1-\alpha _{1}):\alpha _{1}$ . Entsprechendes gilt für die anderen 3 Projektionen.

Satz von Commandino

: Schwerpunkt des Tetraeders,
$S_{i}$ : Schwerpunkte der Dreiecke

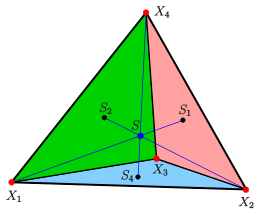
Projiziert man den geometrischen Schwerpunkt $S=(1:1:1:1)$ von $X_{1}=(1:0:0:0)$ aus auf die gegenüberliegende Ebene mit der Gleichung $a_{1}=0$ , erhält man den Schwerpunkt $S_{1}=(0:1:1:1)$ des Dreiecks $X_{2}X_{3}X_{4}$ . Entsprechendes gilt für die anderen Projektionen von . Also gilt (siehe den vorigen Abschnitt):

Die Gerade durch die Ecke $X_{i}$ und den geometrischen Schwerpunkt des Tetraeders schneidet die gegenüberliegende Dreiecksebene im Schwerpunkt $S_{i}$ des Dreiecks. Dabei teilt die Strecke $X_{i}S_{i}$ im Verhältnis $3:1$ .

Dies ist der Satz von Commandino.

Hyperboloid durch die Punkte eines Tetraeders

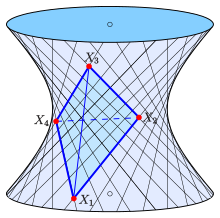
Tetraeder auf einem einschaligen Hyperboloid

Ein einschaliges Hyperboloid ist eine Quadrik, die 2 Scharen von Geraden enthält. In geeigneten homogenen Koordinaten kann man es durch die Gleichung

(H) $\quad a_{1}a_{3}-a_{2}a_{4}=0$

beschreiben (siehe einschaliges Hyperboloid). Das Hyperboloid enthält die Punkte

$X_{1}=(1:0:0:0),\;X_{2}=(0:1:0:0),$

$X_{3}=(0:0:1:0),\;X_{4}=(0:0:0:1)\ .$

Man rechnet leicht nach, dass

(PH) $\quad P(u,v)={\big (}(1-u)(1-v):u(1-v):uv:(1-u)v{\big )}$

eine Parameterdarstellung des Hyperboloids ist. Dabei gilt:

$X_{1}=P(0,0),\ X_{2}=P(1,0),\ X_{3}=P(1,1),\ X_{4}=P(0,1)\$ und

$S=(1:1:1:1)=P({\tfrac {1}{2}},{\tfrac {1}{2}})\ .$

Die Parameterlinien (= const oder = const) sind Geraden. Da die Summe der baryzentrischen Koordinaten stets ist, werden allerdings die Punkte des Hyperboloids in der Ebene $a_{1}+a_{2}+a_{3}+a_{4}=0$ nicht erfasst. Dies ist bei Einführung baryzentrischer Koordinaten kein Nachteil.

Fasst man $a_{1},a_{2},a_{3},a_{4}$ als baryzentrische Koordinaten auf, entsprechen die Punkte $X_{1},X_{2},X_{3},X_{4}$ den Ecken eines Tetraeders (in einem affinen Raum) auf einem Hyperboloid ${\mathcal {H}}$ , das die Geraden ${\overline {X_{1}X_{2}}},{\overline {X_{2}X_{3}}},{\overline {X_{3}X_{4}}},{\overline {X_{4}X_{1}}}$ enthält (siehe Bild). Die beiden Geraden ${\overline {X_{2}X_{4}}},{\overline {X_{1}X_{3}}}$ liegen nicht auf dem Hyperboloid ! Rechnet man die normierten baryzentrischen Koordinaten in affine Koordinaten um (siehe (S) im Abschnitt Definition), erhält man die affine Parameterdarstellung des Hyperboloids:

(APH) $\quad \mathbf {p} (u,v)=(1-u)(1-v)\mathbf {x} _{1}+u(1-v)\mathbf {x} _{2}+uv\mathbf {x} _{3}+(1-u)v\mathbf {x} _{4}\ .$

Dies ist die Darstellung des Hyperboloids als bilineare Interpolationsfläche des räumlichen Vierecks $X_{1},X_{2},X_{3},X_{4}$ .

Eigenschaften

Das Hyperboloid hat mit der Fernebene $a_{1}+a_{2}+a_{3}+a_{4}=0$ die beiden sich im Punkt $A=(1:-1:1:-1)$ schneidenden Geraden

$g_{1}:a_{1}+a_{2}=0,\;a_{3}+a_{4}=0,$

$g_{2}:a_{2}+a_{3}=0,\;a_{1}+a_{4}=0\;$

gemeinsam und ist deshalb affin ein

hyperbolisches Paraboloid. (Das obige Bild ist also projektiv zu verstehen.)
Die Fernebene ist die Tangentialebene im Punkt .
Der Schwerpunkt $S=(1:1:1:1):{\tfrac {1}{4}}(\mathbf {x} _{1}+\mathbf {x} _{2}+\mathbf {x} _{3}+\mathbf {x} _{4})$ des Tetraeders liegt auf dem Hyperboloid.

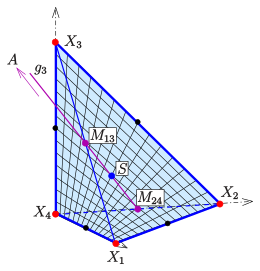
Hyperbolisches Paraboloid (affiner Teil eines projektiven einschaligen Hyperboloids) durch die Ecken eines Tetraeders mit Punkten auf den Koordinatenachsen

Die Gerade $\;g_{3}:a_{1}-a_{3}=0,\;a_{2}-a_{4}=0\;$ geht durch die Mittelpunkte $M_{13}=(1:0:1:0),\;M_{24}=(0:1:0:1)$ der Tetraederkanten $X_{1}X_{3}$ bzw. $X_{2}X_{4}$ und durch den Fernpunkt $A=(1:-1:1:-1)$ . Dies bedeutet affin:

Die Achsen der Parabeln auf dem hyperbolischen Paraboloid sind alle parallel zur Gerade $g_{3}$ durch die Mittelpunkte $M_{13}:{\tfrac {1}{2}}(\mathbf {x} _{1}+\mathbf {x} _{3}),\;M_{24}:{\tfrac {1}{2}}(\mathbf {x} _{2}+\mathbf {x} _{4})$ (siehe hyperbolisches Paraboloid). Der Schwerpunkt ist der Mittelpunkt der Punkte $M_{13},M_{24}$ .

Beispiel

Das Bild zeigt das Beispiel mit

$\mathbf {x} _{1}=(1,0,0)^{T},\;\mathbf {x} _{2}=(0,1,0)^{T},\;$

$\mathbf {x} _{3}=(0,0,1)^{T},\;\mathbf {x} _{4}=(0,0,0)^{T},\;$

Die Parameterdarstellung ist dann

$\mathbf {p} (u,v)={\big (}(1-u)(1-v),u(1-v),uv{\big )}^{T}\ .$

Verallgemeinerte baryzentrische Koordinaten

Baryzentrische Koordinaten $(a_{1},\dotsc ,a_{n})$ , die mit Bezug auf ein Polytop statt mit Bezug auf ein Simplex definiert sind, werden verallgemeinerte baryzentrische Koordinaten genannt. Hierbei wird weiterhin verlangt, dass die Gleichung

$(a_{1}+\dotsb +a_{n})\mathbf {p} =a_{1}\,\mathbf {x} _{1}+\dotsb +a_{n}\,\mathbf {x} _{n}$

erfüllt wird, wobei $\mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}$ hier die Eckpunkte des gegebenen Polytops sind. Die Definition ist also formal unverändert, allerdings muss ein Simplex mit Eckpunkten in einem Vektorraum mit einer Dimension von mindestens n-1 enthalten sein, während Polytope auch in Vektorräume von niedrigerer Dimension eingebettet sein können. Das einfachste Beispiel ist ein Viereck in der Ebene. Als Konsequenz sind sogar die normierten verallgemeinerten baryzentrischen Koordinaten für ein Polytop im Allgemeinen nicht eindeutig bestimmt, obwohl dies für normierte baryzentrische Koordinaten mit Bezug auf ein Simplex der Fall ist.

Verallgemeinerte baryzentrische Koordinaten werden insbesondere in der Computergrafik und bei der geometrischen Modellierung verwendet. Dort können dreidimensionale Objekte oft durch Polyeder approximiert werden, sodass die verallgemeinerten baryzentrischen Koordinaten eine geometrische Bedeutung haben und die weitere Bearbeitung dieser Objekte erleichtern.

Baryzentrische Interpolation

Auf baryzentrischen Koordinaten basiert ein Interpolationsverfahren, das die lineare Interpolation für Funktionen mehrerer Variablen verallgemeinert.

Im Falle einer Funktion von zwei Variablen und sind für drei Punkte A(x_A,y_A) , B(x_B,y_B) und C(x_C,y_C) die Funktionswerte gegeben. Dabei dürfen , und nicht auf einer Geraden liegen. Sie müssen also ein Dreieck ABC aufspannen. Ist nun ein beliebiger Punkt (x,y) gegeben, so definiert man

$f(x,y) = a \, f(x_A,y_A) + b \, f(x_B,y_B) + c \, f(x_C,y_C)$ ,

wobei (a,b,c) die normierten baryzentrischen Koordinaten von (x,y) sind. Diese Interpolation funktioniert auch für Punkte außerhalb des Dreiecks.

Literatur

Oswin Aichholzer, Bert Jüttler: Einführung in die angewandte Geometrie. Springer-Verlag, Basel 2013, doi:10.1007/978-3-0346-0651-6, ISBN 978-3-0346-0651-6.
Gerald Farin, Diane Hansford: Lineare Algebra: Ein geometrischer Zugang. Springer-Verlag, 2013, doi:10.1007/978-3-642-55841-2, ISBN 978-3-540-41854-2 .
John Fauvel, Raymond Flood, Robin Wilson: Möbius und sein Band: Der Aufstieg von Mathematik und Astronomie im Deutschland des 19. Jahrhunderts. Springer-Verlag, 2013, ISBN 978-3-0348-6203-5.
Peter Knabner, Lutz Angermann: Numerik partieller Differentialgleichungen. Eine anwendungsorientierte Einführung. Springer 2000, ISBN 3-642-57181-6.
August Ferdinand Möbius: Der baryzentrische Calcul, Verlag von Johann Ambrosius BartH, Leipzig, 1827.

Basierend auf einem Artikel in:

Wikipedia.de