Ankreis

Dreieck mit Ankreisen (rot)

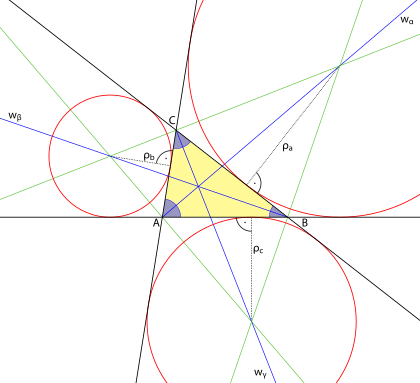
Die drei Ankreise gehören mit dem Umkreis und dem Inkreis zu den besonderen Kreisen eines Dreiecks, die schon in der Antike von griechischen Mathematikern untersucht wurden.

Die Ankreise sind definiert als Kreise, die jeweils von einer Dreiecksseite von außen und von den Verlängerungen der beiden anderen Seiten tangential berührt werden. Jedes beliebige Dreieck besitzt drei Ankreise. Die Ankreismittelpunkte liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der beiden Außenwinkel, die nicht zu dem Innenwinkel gehören.

Radien

Der Radius desjenigen Ankreises, der die Seite ( [BC] ) im Inneren berührt, ergibt sich aus

$\rho _{a}={\frac {A}{s-a}}$ ,

dabei steht für den Flächeninhalt und für den halben Umfang des Dreiecks: $s={\tfrac {1}{2}}(a+b+c)$ .

Analog berechnen sich die Radien $\rho _{b}$ und $\rho _{c}$ der beiden anderen Ankreise.

Drückt man den Flächeninhalt nach dem Satz des Heron durch die Seitenlängen aus, so erhält man

$\rho _{a}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}}$ .

Für die anderen beiden Ankreise gilt entsprechend

$\rho _{b}={\sqrt {\frac {s(s-a)(s-c)}{s-b}}}$ und $\rho _{c}={\sqrt {\frac {s(s-a)(s-b)}{s-c}}}$ .

Berührpunktabstände

Dreieck, Berührpunktabstände der Ankreise, gleichfarbige Abstände haben gleiche Längen

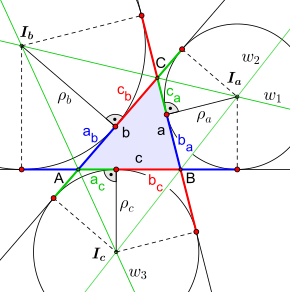
Bezeichnung

ist der Abstand von zu den Berührpunkten des Ankreises mit der Seite und mit der Verlängerung der Seite
ist der Abstand von zu den Berührpunkten des Ankreises mit der Seite und mit der Verlängerung der Seite

Der Index steht dafür, dass derjenige Ankreis betrachtet wird, der die Seite im Dreieck und nicht in der Verlängerung berührt. Analog wird die Bezeichnung für die anderen zwei Ankreise gewählt.

Es gilt:

$a_{b}=b_{a}=s-c.$

Dabei ist der halbe Umfang des Dreiecks.

Addiert man eine Seitenlänge mit einem Berührpunkabstand des Ankreises auf der Seitenverlängerung, ergibt sich $s.$

Beispiel

$c+b_{a}=b+c_{a}=s$

Mittelpunkte

Die Mittelpunkte der Ankreise an ihrer jeweiligen Seite haben folgende baryzentrische Koordinaten, wobei $\displaystyle I_a$ den Mittelpunkt des Ankreises der Seite a repräsentiert:

$\displaystyle I_a = (-a:b:c)$
$\displaystyle I_b = (a:-b:c)$
$\displaystyle I_c = (a:b:-c)$

Konstruktion der Ankreismittelpunkte

Dreieck, Konstruktion der Ankreismittelpunkte

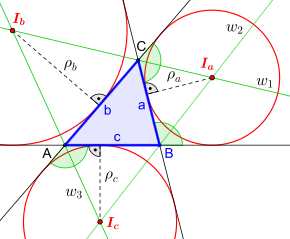
Aus der Einleitung und dem obigen Bild Dreieck mit Ankreisen (rot) kann man folgendes schließen. Die drei Ankreismittelpunkte können auch allein mittels Halbierungen von drei Außenwinkeln gefunden werden, die als Winkelschenkel jeweils eine Seite sowie eine Verlängerung einer benachbarten Seite aufweisen.

Es beginnt mit den Verlängerungen der Seiten des Dreiecks ABC über dessen Eckpunkte hinaus. Danach folgt z.B. die Winkelhalbierende w_1 des Außenwinkels am Scheitel mit den Winkelschenkeln Seite und Verlängerung der Seite ab Die Winkelhalbierende $w_{2}$ des Außenwinkels am Scheitel mit den Winkelschenkeln Seite und Verlängerung der Seite ab schließt sich an und liefert dabei, als Schnittpunkt mit w_1 , den ersten Ankreismittelpunkt $I_{a}.$ Sind alle drei Ankreismittelpunkte gesucht, ist abschließend noch die Winkelhalbierende w_3 des Außenwinkels am Scheitel mit den Winkelschenkeln Seite und Verlängerung der Seite ab erforderlich. Damit ergeben sich, als Schnittpunkte mit den bereits vorhandenen Winkelhalbierenden w_1 und $w_{2},$ auch noch die beiden Ankreismittelpunkte $I_{b}$ und $I_{c}.$

Weitere Eigenschaften

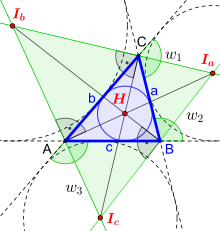
Dreieck $I_{a}\;I_{b}\;I_{c},$ Inkreismittelpunkt

Die Ankreismittelpunkte $I_{a},I_{b}$ und $I_{c}$ des Dreiecks bilden ein Dreieck, dessen Höhenschnittpunkt der Inkreismittelpunkt des Dreiecks ist.
Verbindet man die Ecken eines Dreiecks mit den gegenüberliegenden Berührpunkten der Ankreise, so schneiden sich die Verbindungsgeraden in einem Punkt, dem Nagel-Punkt.

Literatur

H. S. M. Coxeter>, S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983, ISBN 3-12-983390-0.
Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3

Basierend auf einem Artikel in:

Wikipedia.de