Nagel-Punkt

Nagel-Punkt N

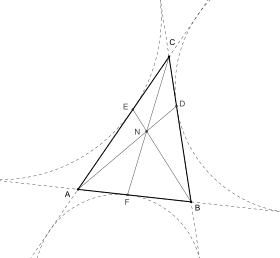
Der Nagel-Punkt, benannt nach dem deutschen Mathematiker Christian Heinrich von Nagel (1803–1882), der 1835/36 die Existenz dieses Punktes aufzeigte, gehört zu den besonderen Punkten eines Dreiecks. Für ein gegebenes Dreieck ABC betrachtet man die Punkte D, E und F, in denen die Ankreise die Seiten des Dreiecks berühren. Verbindet man diese Berührpunkte mit den gegenüber liegenden Ecken des Dreiecks (also mit A, B bzw. C), so schneiden sich diese Verbindungsstrecken in einem Punkt N. Dieser wird als Nagel-Punkt des Dreiecks bezeichnet.

Eigenschaften

Betrachtet man außer dem Nagel-Punkt N des Dreiecks ABC auch den Inkreismittelpunkt I und den Schwerpunkt S, dann liegen die Punkte N, S und I auf einer Geraden, der Nagel-Geraden, und es gilt $\overline {NS}:\overline {SI}=2:1$ , wobei der Schwerpunkt S zwischen den Punkten N und I liegt. In dieser Eigenschaft weist die Nagel-Gerade eine Analogie zur eulerschen Geraden auf.
Der Spieker-Punkt ist der Mittelpunkt der Verbindungsstrecke von Nagel-Punkt und Inkreismittelpunkt und liegt somit ebenfalls auf der Nagel-Geraden.
Der Nagelpunkt und der Gergonne-Punkt sind isotomisch konjugiert.

Koordinaten

Nagel-Punkt ( $X_{{8}}$ )
Trilineare Koordinaten	${\frac {b+c-a}{a}}\,:\,{\frac {c+a-b}{b}}\,:\,{\frac {a+b-c}{c}}$
Baryzentrische Koordinaten	$(b+c-a)\,:\,(c+a-b)\,:\,(a+b-c)$

Basierend auf einem Artikel in:

Wikipedia.de