Winkelhalbierendensatz (Dreieck)

$\gamma_1=\gamma_2\,\Leftrightarrow\,\tfrac{|AC|}{|BC|}=\tfrac{|AD|}{|BD|}$

Der Winkelhalbierendensatz ist eine Aussage der Elementargeometrie. Sie besagt, dass die Winkelhalbierende in einem Dreieck die dem Winkel gegenüberliegende Seite im Verhältnis der beiden am Winkel anliegenden Seiten teilt.

Satz und Verallgemeinerung

In einem Dreieck $\triangle ABC$ sei ein Punkt auf der Seite . Die Strecke teilt den Winkel $\angle ACB$ in die Winkel $\gamma_1 =\angle ACD$ und $\gamma_2 =\angle DCB$ . Sind diese beiden Winkel gleich groß, das heißt ist die Winkelhalbierende des Winkels $\angle ACB$ , dann gilt für die Streckenverhältnisse:

$\frac{|AC|}{|BC|}=\frac{|AD|}{|DB|}$ .

Diese Aussage lässt sich auch auf Strecken verallgemeinern, die den Winkel in einem beliebigen Verhältnis teilen. Es gilt dann die folgende Verhältnisgleichung:

$\frac{|AC|\sin(\gamma_1)}{|BC|\sin(\gamma_2)}=\frac{|AD|}{|DB|}$ .

Es gilt auch die Umkehrung des Winkelhalbierendensatzes. Das heißt, ist ein Punkt auf der Seite eines Dreiecks $\triangle ABC$ und es gilt das Streckenverhältnis ${\tfrac {|AC|}{|BC|}}={\tfrac {|AD|}{|DB|}}$ , dann ist die Winkelhalbierende des Winkels in .

Beweis

Skizze zum Beweis

Ein einfacher Beweis der verallgemeinerten Aussage ergibt sich, indem der Quotient der Flächen der beiden durch die Winkelhalbierenden entstandenen Teildreiecke auf zwei unterschiedliche Arten berechnet wird. Auf die erste Art ergeben sich die Dreiecksflächen nach der Formel ${\tfrac {1}{2}}gh$ mit Grundseite und zugehöriger Höhe , auf die zweite Art nach der Formel ${\tfrac {1}{2}}ab\sin(\gamma )$ mit den beiden Seiten , und dem davon eingeschlossenen Winkel $\gamma$ .

Damit erhält man nun

${\frac {|\triangle ADC|}{|\triangle DBC|}}={\frac {{\frac {1}{2}}|AD|h}{{\frac {1}{2}}|BD|h}}={\frac {|AD|}{|BD|}}$

und

${\frac {|\triangle ADC|}{|\triangle BDC|}}={\frac {{\frac {1}{2}}|AC||CD|\sin(\gamma _{1})}{{\frac {1}{2}}|BC||CD|\sin(\gamma _{2})}}={\frac {|AC|\sin(\gamma _{1})}{|BC|\sin(\gamma _{2})}}$

also gilt

${\frac {|AC|\sin(\gamma _{1})}{|BC|\sin(\gamma _{2})}}={\frac {|AD|}{|BD|}}$

Zu einem Beweis mit baryzentrischen Koordinaten: siehe hier.

Außenwinkelhalbierenden

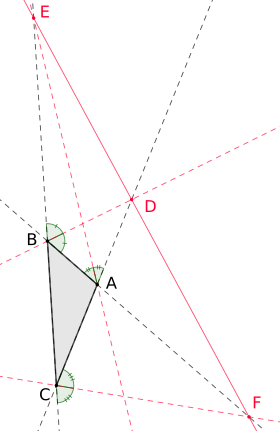
Außenwinkelhablierenden (rot gestrichelt):
Die 3 Schnittpunkte D, E, F liegen auf einer Geraden (rot) und es gelten die folgenden Streckenverhältnisse:
${\tfrac {|EB|}{|EC|}}={\tfrac {|AB|}{|AC|}}$ , ${\tfrac {|FB|}{|FA|}}={\tfrac {|CB|}{|CA|}}$ , ${\tfrac {|DA|}{|DC|}}={\tfrac {|BA|}{|BC|}}$

Sofern es nicht um ein gleichseitiges Dreieck handelt, existieren für die Außenwinkelhalbierenden eines Dreiecks ebenfalls Verhältnisgleichungen, die die Dreiecksseiten beinhalten. Genauer gilt für ein nicht-gleichseitiges Dreieck ABC das Folgende. Schneidet die Außenwinkelhalbierende in , die Verlängerung der Seite in , die Außenwinkelhalbierende in die Verlängerung der Seite in und die Außenwinkelhalbierende in die Verlängerung der Seite in , dann gilt:

${\frac {|EB|}{|EC|}}={\frac {|AB|}{|AC|}}$ , ${\frac {|FB|}{|FA|}}={\frac {|CB|}{|CA|}}$ und ${\frac {|DA|}{|DC|}}={\frac {|BA|}{|BC|}}$

Darüber hinaus liegen die Punkte , und auf einer gemeinsamen Geraden.

Geschichte

Der Winkelhalbierendensatz findet sich bereits bei Euklid in den Elementen im Buch VI als Proposition 3.

Literatur

Siegfried Krauter, Christine Bescherer: Erlebnis Elementargeometrie: Ein Arbeitsbuch zum selbstständigen und aktiven Entdecken. Springer, 2012, ISBN 978-3-8274-3025-0.
Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9.

Basierend auf einem Artikel in:

Wikipedia.de