Zentrische Streckung

Zentrische Streckung mit positivem Streckungsfaktor

Zentrische Streckung mit negativem Streckungsfaktor

Unter einer zentrischen Streckung versteht man in der Geometrie eine Abbildung, die alle Strecken in einem bestimmten, gegebenen Verhältnis vergrößert oder verkleinert, wobei die Bildstrecken jeweils zu den ursprünglichen Strecken parallel sind. Zentrische Streckungen sind spezielle Ähnlichkeitsabbildungen.

Definition

Gegeben seien ein Punkt der Zeichenebene oder des Raumes und eine reelle Zahl $m\neq 0$ . Die zentrische Streckung mit Zentrum und Streckungsfaktor (Abbildungsfaktor) ist diejenige Abbildung der Zeichenebene beziehungsweise des Raumes in sich, bei der der Bildpunkt eines Punktes folgende Eigenschaften besitzt:

, und liegen auf einer Geraden.
Für liegen und auf derselben Seite von , für auf verschiedenen Seiten.
Die Streckenlänge $\overline {ZP'}$ ist gleich dem -fachen der Streckenlänge $\overline{ZP}$ .

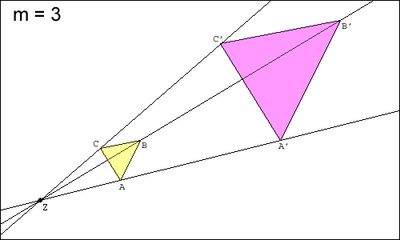
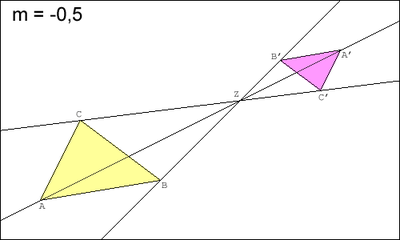
Die beiden Skizzen zeigen die Anwendung zweier zentrischer Streckungen (mit m=3 und m=-0{,}5 ) auf jeweils ein Dreieck ABC.

Eigenschaften

Zentrische Streckungen sind geraden-, kreis- und winkeltreu.
Die Längenverhältnisse bleiben erhalten.
Die Bildstrecke einer beliebigen Strecke hat die -fache Länge.
Eine beliebige geometrische Figur wird auf eine Figur mit dem $m^{2}$ -fachen Flächeninhalt abgebildet.
Ein beliebiger Körper wird auf einen Körper mit dem $|m|^{3}$ -fachen Volumen abgebildet.
Die zentrischen Streckungen mit einem bestimmten Zentrum bilden algebraisch gesehen eine Gruppe.
Das Bild einer Geraden ist eine Parallele zu der Geraden.
In vektorieller Schreibweise wird die zentrische Streckung mit Zentrum und Streckungsfaktor beschrieben durch

Damit ist eine zentrische Streckung die Affinität, die durch die Matrix $mE_{n}$ und den Verschiebungsvektor beschrieben wird.
Auch die identische Abbildung wird als Streckung mit dem Streckfaktor zu den Streckungen gezählt. Eine nichtidentische Streckung hat genau einen Fixpunkt, das ist ihr Streckzentrum, und ihre Fixgeraden sind genau die Geraden, die durch dieses Zentrum gehen.

Spezialfälle

Für m=1 ergibt sich die identische Abbildung (Identität), für m=-1 eine Punktspiegelung. Der Fall m = 0 ist nicht erlaubt, da sonst alle Punkte denselben Bildpunkt hätten, nämlich das Zentrum.

Verallgemeinerungen

Die zentrische Streckung ist ein Beispiel für eine Dilatation. In der axiomatisch aufgebauten affinen Geometrie wird dieser Begriff mithilfe der Parallelität definiert.
Die zentrische Streckung ist der Spezialfall einer Drehstreckung mit Drehwinkel 0.
An Stelle des affinen 2- bzw. 3-dimensionalen Raumes über den reellen Zahlen, kann man zentrische Streckungen auch allgemeiner in jedem endlichdimensionalen affinen Raum über einem beliebigen Körper und sogar über einem beliebigen Schiefkörper definieren. Die „vektorielle“ Darstellung ist die Gleiche wie im reellen Fall, allerdings bilden die Parallelverschiebungen, die von einem Zentrum aus gestreckt werden, im Allgemeinen nur noch einen Linksvektorraum über dem Koordinatenschiefkörper.
Im ebenen, zweidimensionalen Fall wird noch etwas allgemeiner auch noch dann von einer zentrischen Streckung gesprochen, wenn die Parallelverschiebungen (als Koordinaten-„Vektoren“) einer affinen Translationsebene über einem Quasikörper mit einem „Skalar“ aus dem Kern des Quasikörpers gestreckt werden.

In den beiden zuletzt genannten Fällen kann man im Allgemeinen weder von Winkel- noch von Längenverhältnistreue sprechen, da weder ein Winkelmaß noch ein Längenmaß existieren muss. Auch hier gehören die zentrischen Streckungen aber stets zu den Dilatationen und den Affinitäten und für Fixpunkte und Fixgeraden gilt das Gleiche wie im reellen Fall.

Siehe auch

Strahlensatz

Basierend auf einem Artikel in:

Wikipedia.de