Affine Translationsebene

Als affine Translationsebene oder kurz Translationsebene wird in der synthetischen Geometrie eine affine Ebene dann bezeichnet, wenn ihre Translationsgruppe scharf einfach transitiv auf ihr operiert und sie daher weitgehend durch diese Gruppe ihrer Translationen (Parallelverschiebungen) beschrieben werden kann, indem jedem Punkt der Ebene eine Translation zugeordnet wird. Der Endomorphismenring der Translationsgruppe, die bei einer Translationsebene stets kommutativ ist, enthält einen Schiefkörper, den Schiefkörper der spurtreuen Endomorphismen. Die Gruppe der Translationen ist ein Modul über diesem Schiefkörper.

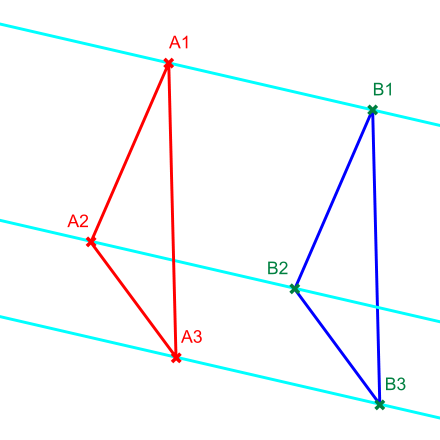
Rein geometrisch ist eine affine Ebene genau dann eine Translationsebene, wenn in ihr der kleine affine Satz von Desargues (vergleiche die Abbildung am Ende der Einleitung) allgemeingültig ist, also ein Schließungssatz, der in der synthetischen Geometrie als Axiom verwendet wird.

Daneben wird in der synthetischen Geometrie seltener der Begriff projektive Translationsebene verwendet. Diese speziellen projektiven Ebenen hängen eng mit den affinen Translationsebenen zusammen. Dieser Zusammenhang wird im vorliegenden Artikel im Abschnitt Projektive Translationsebene erläutert. Die Begriffe affine Translationsebene bzw. projektive Translationsebene sind Verallgemeinerungen der Begriffe desarguessche affine bzw. desarguessche projektive Ebene.

Die Untersuchung der Translationen und ihrer spurtreuen Endomorphismen ist neben der Beschreibung durch einen Koordinatenternärkörper eine gängige Methode, nichtdesarguesche Ebenen zu algebraisieren. Für desarguesche und erst recht für pappussche Ebenen fällt der Schiefkörper der spurtreuen Endomorphismen mit dem Koordinatenschiefkörper zusammen, bei Translationsebenen ist er im Koordinatenquasikörper als Kern enthalten.

Die Algebraisierung einer affinen Ebene mithilfe von Koordinaten auf einer Geraden der Ebene, algebraische Verknüpfungen dieser Koordinaten sowie die Begriffe Ternärkörper und Quasikörper, die im vorliegenden Artikel verwendet werden, sind in den entsprechenden Hauptartikeln ausführlicher dargestellt.

Der kleine affine Satz von Desargues besagt: Sind $A_{1}A_{2}A_{3}$ und $B_{1}B_{2}B_{3}$ Dreiecke, bei denen die „Zuordnungsgeraden“ parallel sind: $A_{1}B_{1}\parallel A_{2}B_{2}\parallel A_{3}B_{3}$ dann folgt aus der Parallelität von zwei Paaren von Dreiecksseiten (z.B. $A_{1}A_{2}\parallel B_{1}B_{2}$ und $A_{2}A_{3}\parallel B_{2}B_{3}$ ), dass auch das dritte Seitenpaar parallel ist (im Beispiel $A_{3}A_{1}\parallel B_{3}B_{1}$ ).

Definitionen und Eigenschaften

Translationen in affinen Inzidenzebenen

Eine bijektive Selbstabbildung $\tau :{\mathcal A}\rightarrow {\mathcal A}$ einer affinen Ebene $\mathcal A$ heißt Translation, wenn gilt

das Bild jeder Geraden ist eine Gerade, d.h. $\tau$ ist eine Kollineation
für jede Gerade der Ebene ist $\tau (g)\parallel g$ ,
$\tau$ ist fixpunktfrei oder die identische Abbildung der Ebene $\mathcal A$ , $\;\operatorname {Id}_{{{\mathcal A}}}$ .

Jede Translation $\tau$ ist durch ein Punkt-Bildpunkt-Paar $(P,\tau (P))\in {\mathcal {A}}^{2}$ eindeutig bestimmt.

Für nichtidentische Translationen ist die Verbindungsgerade von und $\tau (P)$ eine Spurgerade. Genau die Parallelen dieser Geraden bilden die Menge aller Spuren von $\tau$ . Die Parallelenschar der Spuren heißt Richtung der Translation $\tau$ und man nennt $\tau$ dann auch eine Verschiebung in Richtung .

Translationsgruppe und spurtreue Endomorphismen

Die Menge der Translationen einer affinen Inzidenzebene bildet bezüglich der Komposition eine Gruppe $({\mathcal {T}},\circ )$ . Diese Gruppe ist kommutativ, falls es (nichtidentische) Translationen der Ebene in (mindestens) zwei unterschiedliche Richtungen gibt. Ein Gruppenendomorphismus $\alpha :{\mathcal {T}}\rightarrow {\mathcal {T}}$ heißt spurtreu, wenn für jede nichtidentische Translation $\tau \in {\mathcal {T}}\setminus \lbrace \operatorname {Id}_{{{\mathcal A}}}\rbrace$ die Spuren von $\tau$ mit den Spuren von $\alpha (\tau )$ übereinstimmen oder $\alpha$ der 0-Endomorphismus $0_{S}:\tau \mapsto \operatorname {Id}_{{{\mathcal A}}}$ ist. Gleichwertig: $\alpha$ ändert bei keiner Translation deren Richtung.

Ist die Translationsgruppe kommutativ und nichttrivial, ^[1] dann wird die Menge der spurtreuen Endomorphismen durch die Verknüpfungen

$\alpha +\beta :\tau \mapsto \alpha (\tau )\circ \beta (\tau )\quad$ und

$\alpha \cdot \beta :\tau \mapsto \alpha (\beta (\tau ))\quad$

zu einem Ring mit Nullement $0_{S}:\tau \mapsto \operatorname {Id}_{{{\mathcal A}}}$ und Einselement $1_{S}=\operatorname {Id}_{{{\mathcal {T}}}}$ , einem Unterring des Endomorhismenringes. Die Reihenfolge, in der die Homomorphismen in der Definition der Multiplikation auf Translationen angewendet werden, bestimmt, ob die Translationsgruppe zu einem Links- oder Rechtsmodul über wird. Bei der hier gewählten Definition $\alpha \cdot \beta =\alpha \circ \beta$ und $\alpha \cdot \tau =\alpha (\tau )$ für die „Skalarmultiplikation“ ist sie ein -Linksmodul.

Affine Translationsebene

Eine affine Inzidenzebene heißt affine Translationsebene, wenn eine der folgenden äquivalenten Bedingungen zutrifft:

Der kleine affine Satz von Desargues gilt in $\mathcal A$ .
Der Koordinatenternärkörper, der $\mathcal A$ durch Wahl eines beliebigen Koordinatensystems zugeordnet werden kann, ist ein Quasikörper.
Zu zwei Punkten $P,Q\in A$ gibt es stets eine Translation $\tau \in {\mathcal {T}}$ mit $\tau (P)=Q$ .
Die Translationsgruppe operiert scharf einfach transitiv auf $\mathcal A$ .

Damit gibt es in einer affinen Translationsebene $\mathcal A$ , wenn man einen Punkt $O\in {\mathcal A}$ als Ursprung fest wählt, eine natürliche Bijektion ${\mathcal A}\ni P\leftrightarrow \tau _{P}\in {\mathcal {T}}:\tau _{P}(O)=P$ zwischen den Punkten der Ebene und der Translationsgruppe. Eine Translationsebene kann so mit ihrer Translationsgruppe identifiziert werden.

Andererseits kann jede Translation mit einer Äquivalenzklasse von verschiebungsgleichen geordneten Punktepaaren („Pfeilen“) identifiziert werden, dabei sind zwei Pfeile $(P_{1},Q_{1}),(P_{2},Q_{2})\in {\mathcal A}^{2}$ äquivalent, wenn $\tau (P_{1})=Q_{1}$ und $\tau (P_{2})=Q_{2}$ mit derselben Translation $\tau \in {\mathcal {T}}$ gilt. Man nennt diese Äquivalenzklassen von Pfeilen auch „Vektoren“.

Für die eindeutig bestimmte Translation, die einen Punkt auf einen Punkt abbildet, wird abkürzend ${\overrightarrow {PQ}}$ geschrieben. Diese Schreibweise bezeichnet zugleich die Äquivalenzklasse der zu (P,Q) verschiebungsgleichen „Pfeile“.

Da bei einer Translationsebene jeder spurtreue Endomorphismus $\alpha \in S\setminus \lbrace 0\rbrace$ sogar ein Gruppenautomorphismus ist, ist der Ring $(S,+,\cdot )$ hier sogar ein Schiefkörper. Die Gruppe der Translationen („Vektoren“ im oben beschriebenen Sinn) bilden einen -Linksmodul. Lässt man als Skalarkörper eines Vektorraums auch einen Schiefkörper zu, wie das gelegentlich in der Literatur geschieht, so bildet die Gruppe der Translationen also tatsächlich einen -Linksvektorraum.

Als Folge davon ist die Ordnung jeder nichtidentischen Translation $\tau \in {\mathcal {T}}$ durch die Charakteristik von bestimmt: Ist diese Charakteristik eine Primzahl , dann haben alle nichtidentischen Translationen diese Ordnung , ist sie 0, dann haben alle nichtidentischen Translationen unendliche Ordnung. Genau dann, wenn die Charakteristik von 2 verschieden ist, erfüllt die Translationsebene das (affine) Fano-Axiom.

Koordinatenquasikörper und spurtreue Endomorphismen

Kern des Koordinatenquasikörpers

Ein (Links-)Quasikörper unterscheidet sich von einem Schiefkörper dadurch, dass kein Rechtsdistributivgesetz und kein Assoziativgesetz der Multiplikation gefordert wird. Definiert man für einen Quasikörper

$\operatorname {Kern} (K)=\lbrace x\in K:\;\forall a,b\in K\left((a+b)x=ax+bx\land (ab)x=a(bx)\right)\rbrace$

als seinen Kern, dann bildet dieser Kern einen Schiefkörper und dieser ist isomorph zum Schiefkörper der spurtreuen Endomorphismen von ${\mathcal {T}}({\mathcal A})$ zur Translationsebene ${\mathcal A}=K^{2}$ über . Über diesen Isomorphismus wird auch der Koordinatenquasikörper zu einem -Linksmodul, der zu dem Untermodul der Translationen in Richtung der ersten Koordinatenachse in der Translationsgruppe ${\mathcal {T}}({\mathcal A})$ isomorph ist.

Hat man die Multiplikation in als $\alpha \cdot \beta =\beta \circ \alpha$ definiert und die „Skalarmultiplikation“ von rechts als $\tau \cdot \alpha =\alpha (\tau ),$ dann muss für den Isomorphismus $S\cong \operatorname {Kern}(K)$ die Multiplikation nicht umgekehrt werden, da die Elemente des Kerns nach Konstruktion auch von rechts distributiv und assoziativ operieren und wird dann zu einem -Rechtsmodul. Es ist aber in der Literatur üblich, nur Rechtsquasikörper – bei denen die Definition des Kerns entsprechend angepasst werden muss – mit einer solchen Rechtsmodulstruktur zu versehen, da sich bei „gleichseitiger“ Struktur zwangloser eine geometrische Deutung von S^* als Gruppe von geometrischen Abbildungen ergibt.

Kommensurable Punkte, Streckungsfaktor, Teilverhältnis

Drei kollineare Punkte A,B,C der Translationsebene $\mathcal A$ nennt man kommensurabel, wenn ein spurtreuer Endomorphismus $\alpha \in S$ existiert, der die Translation, die auf verschiebt, in die Translation verwandelt, die auf verschiebt. Vektoriell geschrieben: $\alpha (\overrightarrow {AB})=\overrightarrow {AC}$ . In diesem Fall nennt man $\alpha \in S$ den Streckungsfaktor $\alpha =\operatorname {SF}(A,B,C)$ zu dem Punktetripel (A,B,C) . Aus dem Streckungsfaktor kann (für drei verschiedene kollineare und kommensurable Punkte) umkehrbar eindeutig ein Teilverhältnis $\lambda =\operatorname {TV}(ABC)\in S$ gewonnen werden:

$\alpha ={\frac {\lambda }{1+\lambda }},\quad \lambda ={\frac {\alpha }{1-\alpha }}.$

Die Bruchschreibweise ist hier unproblematisch, da alle auftretenden Elemente von untereinander kommutieren.

Strahlensatz und Streckungen

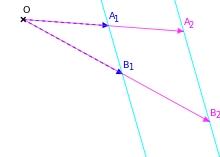
Zum Strahlensatz für Translationsebenen.

Sind $O,A_{1},A_{2},B_{1},B_{2}$ fünf Punkte einer affinen Translationsebene mit den Eigenschaften (vgl. die Abbildung rechts):

$O,A_{1},B_{1}$ sind nicht kollinear,
$O,A_{1},A_{2}$ sind kollinear und kommensurabel,
$O,B_{1},B_{2}$ sind kollinear,

dann gilt: $A_{1}B_{1}\parallel A_{2}B_{2}\;\Leftrightarrow \;{\begin{cases}(O,B_{1},B_{2})\quad {\mbox{sind kommensurabel und}}\\\operatorname {SF} (O,A_{1},A_{2})=\operatorname {SF} (O,B_{1},B_{2})\end{cases}}$

Dieser erste Strahlensatz für Translationsebenen rechtfertigt es, die spurtreuen Endomorphismen als „Zentrische Streckungen“ der Translationsebene zu bezeichnen und motiviert die Bezeichnung „Streckungsfaktor“: Wählt man einen Ursprung $O\in {\mathcal A}$ und ordnet wie oben ausgeführt jedem Punkt die Translation $\overrightarrow{OP}$ zu, dann operiert jeder „Streckungsfaktor“ $\alpha \in S\setminus \lbrace 0,1\rbrace$ auf den Punkten der Ebene als Kollineation und sogar als Dilatation. Bei dieser Dilatation ist der Ursprung Fixpunkt und alle Geraden durch den Ursprung sind Fixgeraden. Umgekehrt operiert jede Dilatation, die genau den Ursprung als Fixpunkt hat, durch Konjugation auf den Translationen und diese Operation ist ein spurtreuer Endomorphismus der Translationsgruppe. Daher sind bei einer Translationsebene die Untergruppe $\Delta _{O}({\mathcal {A}})$ der verallgemeinerten Streckungen mit Zentrum und die Untergruppe der hier beschriebenen Streckungen um mit einem Streckungsfaktor aus $S^{\ast }$ identische Untergruppen der Affinitätengruppe.

Es folgt weiter: Sind in der oben dargestellten Konfiguration $OA_{1}B_{1}$ und $OA_{2}B_{2}$ Dreiecke, $O,A_{1},A_{2}$ und $O,B_{1},B_{2}$ jeweils kollinear und gilt $A_{1}A_{2}\parallel B_{1}B_{2}$ , dann sind von den kollinearen Tripeln $(O,A_{1},A_{2})$ $(O,B_{1},B_{2})$ entweder beide kommensurabel oder beide inkommensurabel. Sind sie inkommensurabel, dann existiert keine Dilatation, die als Fixpunkt hat und $A_{1}$ auf $A_{2}$ , B_1 auf B_2 abbildet. Damit kann auch keine Affinität mit dieser Eigenschaft existieren!

Da der Streckungsfaktor als Abbildung auf die Parallelverschiebungen wirkt, ergibt sich unter den Voraussetzungen des ersten Strahlensatzes und der zusätzlichen Voraussetzung $A_{1}B_{1}\parallel A_{2}B_{2}$ eine dem zweiten Strahlensatz entsprechende Aussage: $\operatorname {SF}(O,A_{1},A_{2})\cdot \overrightarrow {A_{1}B_{1}}=\overrightarrow {A_{2}B_{2}}$ - diese Formel bleibt auch im Trivialfall $\operatorname {SF}(O,A_{1},A_{2})=1$ richtig. Die ersten beiden Strahlensätze gelten also sinngemäß in jeder desargueschen Ebene, wobei dann die Bedingung der Kommensurabilität entfallen kann, ganz allgemein, während der dritte Strahlensatz, der in der synthetischen Geometrie auch Dreistrahlsatz genannt wird, nur für pappussche Ebenen allgemein bewiesen werden kann.

(Vergleiche die Hauptartikel Zentrische Streckung und Strahlensatz)

Desarguesche Ebenen

Eine Translationsebene $\mathcal A$ mit zugehörigem Schiefkörper der spurtreuen Endomorphismen von ${\mathcal {T}}({\mathcal A})$ ist genau dann eine desarguesche Ebene, wenn eine der folgenden äquivalenten Bedingungen zutrifft:

Der große affine Satz von Desargues gilt in $\mathcal A$ .
Ein Koordinatenquasikörper von $\mathcal A$ stimmt mit seinem Kern überein.
Ein Koordinatenquasikörper von $\mathcal A$ ist ein Schiefkörper.
Ein Koordinatenquasikörper von $\mathcal A$ ist isomorph zu .
Liegen drei Punkte der Ebene auf einer Geraden, so sind sie stets kommensurabel.
Die Translationen bilden einen zweidimensionalen Linksvektorraum über .

Da die Koordinatenbereiche durch die affine Ebene bis auf Isomorphie eindeutig bestimmt sind, können die Aussagen über diese Bereiche „Ein Koordinatenquasikörper...“ hier gleichwertig auch mit „Jeder Koordinatenquasikörper...“ formuliert werden.

Andererseits enthält jede „echte“, also nichtdesarguesche Translationsebene eine desarguesche Ebene als echte Teilmenge: Wählt man ein Koordinatensystem (O,E_1,E_2) und betrachtet nur Punkte mit Koordinaten $x_{1},x_{2}\in OE_{1}=K$ , die zu 0=O und $1=E_{1}$ kommensurabel sind, und nur solche Geraden, deren Koeffizienten diese Eigenschaft haben, dann erhält man eine zur desargueschen Ebene $\operatorname {Kern}(K)^{2}$ isomorphe affine Inzidenzstruktur.

Pappussche Ebenen

Wenn sich in einer Translationsebene eine Orthogonalitätsrelation definieren lässt und die Charakteristik des Schiefkörpers nicht 2 ist, das heißt, das (affine) Fano-Axiom gilt, dann ist die Allgemeingültigkeit des Höhenschnittpunktsatzes und des Mittellotensatzes äquivalent und – falls diese allgemeingültig sind – ist in der Ebene der Satz von Pappos allgemeingültig und der Koordinatenquasikörper sogar ein Körper. (Siehe Präeuklidische Ebene).

Allgemein erfüllt eine Translationsebene den Satz von Pappos genau dann,

wenn sie desarguessch ist und die Multiplikation im Schiefkörper der spurtreuen Endomorphismen der Translationsgruppe kommutativ ist, also ein Körper ist oder gleichwertig
wenn ihr Koordinatenquasikörper ein Körper ist.

Ist die Ordnung der Translationsebene endlich, dann ist der Schiefkörper stets ein Körper. Dann ist die Translationsebene genau dann pappussch, wenn sie desarguessch ist.

Endliche Ebenen

Eine affine oder projektive Ebene heißt endlich, wenn es ihre Ordnung und damit auch die Anzahl der Punkte der Ebene ist. Die Ordnung ist bei einer affinen Ebene die Anzahl der Punkte auf einer Geraden, bei einer projektiven Ebene die Ordnung der affinen Ebene, die durch Schlitzen der projektiven Ebene entsteht. Aus der Tatsache, dass der Koordinatenquasikörper einer affinen Translationsebene ein Linksvektorraum über dem Schiefkörper der spurtreuen Endomorphismen ist, ergeben sich zusammen mit dem Satz von Wedderburn, der besagt, dass ein endlicher Schiefkörper stets kommutativ, also ein endlicher Körper ist, Folgerungen für die endlichen Translations- und Moufangebenen:

Der Schiefkörper einer endlichen Translationsebene ist ein endlicher Körper $\mathbb {F} _{q}$ , hat also $q=p^{m}$ Elemente mit einer Primzahl und $m\in \mathbb{N} ,m\geq 1$ .
Der Koordinatenquasikörper ist ein endlichdimensionarer Vektorraum über $S={\mathbb F}_{q}$ und hat demnach $q^{r}=p^{{mr}}\!\,\,(r\in \mathbb{N} ,r\geq 1)$ Elemente. Also ist die Ordnung der Translationsebene diese Primzahlpotenz, ist dabei , dann ist die Translationsebene die pappussche Ebene $S^{2}$ über dem Körper $S={\mathbb F}_{q}$ .
Es existieren zahlreiche endliche affine Translationsebenen, die nicht desarguesch sind, zum Beispiel 4 verschiedene (nicht isomorphe) der Ordnung 9. (Siehe die Beispiele im Artikel Ternärkörper.)
Das formale Analogon zu affinen Translationsebenen unter den projektiven Ebenen sind die Moufangebenen, in denen der kleine projektive Satz von Desargues allgemeingültig ist. Ruth Moufang hat gezeigt, dass echte, das heißt nichtdesarguesche Moufangebenen stets unendlich sind. Daraus folgt, dass bei einer endlichen affinen Translationsebene die projektive Erweiterung genau dann eine Moufangebene ist, wenn beide Ebenen desarguesch und also gleichwertig dazu Ebenen über einem endlichen Körper sind.

Allgemeinere Aussagen über die möglichen Ordnungen endlicher Ebenen finden sich in den Artikeln Projektive Ebene und Projektive Geometrie.

Projektive Translationsebene

Eine projektive Ebene heißt Translationsebene bezüglich einer ihrer Geraden, wenn sie in Bezug auf diese Gerade als Achse den kleinen projektiven Satz von Desargues erfüllt. Eine gleichwertige Beschreibung einer solchen projektiven Translationsebene: Sie gehört zu einer der Klassen IVa, V oder VII in der Klassifikation projektiver Ebenen nach Hanfried Lenz.

Der projektive Abschluss einer affinen Translationsebene ist stets eine projektive Translationsebene. Wenn andererseits eine projektive Translationsebene entlang einer projektiven Geraden geschlitzt wird, entsteht eine affine Ebene, in der diese Gerade die Ferngerade darstellt. Die so erzeugte affine Ebene ist genau dann eine affine Translationsebene, wenn die projektive Ebene den kleinen projektiven Satz von Desargues in Bezug auf als Achse erfüllt. Gleichwertig: Die Gerade muss eine Achse in der Lenz-Figur der projektiven Ebene sein.

Beispiele und Gegenbeispiele

Jede desarguesche Ebene ist eine Translationsebene, also insbesondere die affine Ebene $K^{2}$ über einem Schiefkörper . Hier stimmt der Schiefkörper der spurtreuen Endomorphismen (bis auf Isomorphie) mit dem Koordinatenschiefkörper überein.
Die reellen Oktonionen $\mathbb {O}$ bilden einen Quasikörper, der kein Schiefkörper ist: Zwar gelten beide Distributivgesetze, aber die Multiplikation ist nicht assoziativ. Damit ist die affine Translationsebene ${\mathbb {O}}^{2}$ eine nichtdesarguesche Translationsebene.
Die reelle Moulton-Ebene ist eine affine Ebene, die keine Translationsebene ist: Ist die („normale“ und Moulton-Ebenen-) Gerade, auf der einige Moultongeraden ihren „Knick“ haben, dann besteht die Translationsgruppe genau aus den „normalen“ Verschiebungen der reellen Ebene in Richtung der Geraden , sie ist damit zur kommutativen Gruppe $(\mathbb{R} ,+)$ isomorph. Jeder Gruppenautomorphismus von $(\mathbb{R} ,+)$ ist spurtreu, da aber die Translationsgruppe nicht einfach transitiv auf der Moulton-Ebene operiert, nützt das zur Beschreibung dieser Geometrie wenig.
Dagegen sind die endlichen Moultonebenen stets affine Translationsebenen. Es existieren unendlich viele nichtdesarguesche endliche Translationsebenen dieses Typs, siehe dazu den Abschnitt Quasikörper endlicher Moulton-Ebenen im Artikel Quasikörper.

Der Artikel Ternärkörper enthält weitere Beispiele für affine Translationsebenen, insbesondere auch ausführlich dargestellte Beispiele für endliche, nichtdesarguesche Translationsebenen (siehe im Unterabschnitt Beispiele der Ordnung 9).

Literatur

Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. 1. Auflage. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.
Günter Pickert: Axiomatische Begründung der ebenen euklidischen Geometrie in vektorieller Darstellung. In: Mathematisch-physikalische Semesterberichte. Band 10, 1963, ISSN 0025-5823, S. 65–85.

Anmerkungen

↑ Die Translationsgruppe ist genau dann trivial, also die einelementige Gruppe, wenn es außer der identischen Abbildung keine Translation gibt. In diesem Fall ist die Translationsgruppe kommutativ, aber ihr einziger Endomorphismus ist die Identität, der hier definierte Ring der spurtreuen Endomorphismen wäre also ein Nullring.

Basierend auf einem Artikel in:

Wikipedia.de